Econ 474 - Econometrics of Policy Evaluation

# Econ 474 - Econometrics of Policy Evaluation
## Difference-in-Differences
### Marcelino Guerra
### March 21-30, 2022

---

# Example: Monetary Policy and the Great Depression I

* The U.S. economy appeared to recover after the stock market crash in 1929. However, in the fall 1930, a series of crises among commercial banks contributed to the start of the Great Depression
  
* At that time, there was no deposit insurance. Most likely, in case your bank went out of business, your savings would disappear with it

* Bank is a business based on confidence and trust

* Banks lend to businesses and property owners and expect most loans to be paid off when they come due. Depositors trust they will be able to withdraw their funds at the time they want

* Since banks hold less cash than needed to pay all depositors when confidence falls, the banking system breaks down (self-fulfilling prophecy)
   
]

![](figs/bank.jpg)
.small[**A crowd of depositors outside the American Union Bank in New York, having failed to withdraw their savings before the bank collapsed, 30th June 1931. Source: [Richardson (2013)](https://www.federalreservehistory.org/essays/banking-panics-1930-31). **]

]

---
# Example: Monetary Policy and the Great Depression II

.pull-left[
* The largest Southern banking chain in the 1920s was Caldwell and Company, based in Nashville-TN. The regional empire owned many non-banking businesses as well and collapsed on November 7, 1930

* Within the next few days, correspondent networks toppled like dominoes in Tennessee, Arkansas, Illinois, and North Carolina. Cadwell's demise shook depositor confidence across the American South and precipitated a run on Mississippi banks in December 1930

* The regional panic of 1930 was one of many more to come. In 1933, the number of suspensions peaked, and more than 4,000 banks failed nationwide
]

![](figs/bank2.png)
.small[**Total number of bank suspensions, from 1921 to 1936. The vertical line at 1929 indicates the beginning of the stock market crash. A second vertical line at 1933 indicates the banking holiday of 1933. Source: [Richardson (2013)](https://www.federalreservehistory.org/essays/banking-panics-1930-31).**]

]

---

---
# The Federal Reserve System

* Policymakers facing a bank run have two options: open the flow of cash or turn off the tap
  
  * Easy money might have allowed banks to meet withdrawal demands during the confidence crisis
  
  * But some crises are real - banks might become insolvent because of the economy's contraction and the rise of loan default rates. In this case, the Fed could do little to aid banks. Also, bad debts shouldn't be supported by liquidity support. It is better to declare bankruptcy in case of bad management because support for bad banks can create *moral hazard*
  
* To analyze the impact of Federal Reserve policies, one needs to **find a group of banks that operated in a single regulatory and economic environment but were exposed to different Federal Reserve policy regimes**

]

![](maps/fed_full.gif)
.small[**Distribution of Federal Reserve System. Black squares represent Federal Reserve Bank cities. The star refers to the Board of Governors of the Federal Reserve System in Wahsington D.C.**]
]

---
# Two Mississipi

* During the depression era, the regional Feds had considerable policy independence. The Atlanta Fed (Sixth District) favored lending troubled banks. On the other hand, St. Louis Fed (Eighth District) restricted credit during the recession

* The border between the Sixth and Eighth Districts runs through the middle of the state of Mississippi

* Those two Districts reacted to the Caldwell crisis differently. Within four weeks of Caldwell's collapse, the **Atlanta Fed had increased bank lending by 40% in the Sixth District**, while **bank lending by the St. Louis Fed fell almost 10% in the Eighth District**

]

.pull-right[
<div class="box">
  <iframe src="maps/fed_ms.html" frameborder="0" scrolling="no" width="100%" height="500px" align="right"></iframe>
</div>
]

---

# Monetary Policy and Bank Failures I

* One can think about that as a natural experiment where the Eighth District is the control group, where the policy was to do little or even restrict lending, while the Sixth District is the treatment group, where the policy was to increase lending<sup>1</sup>

* The first step is to see whether different monetary policies led to varying outcomes in terms of bank suspensions. For instance, in 1931, the Mississippi area governed by the Atlanta Fed had 121 banks operating while the area under the St. Louis Fed administration had 132. This would suggest that the monetary policy was counterproductive

* However, those districts were similar but not identical: in 1930, District 8 had 165 banks operating while District 6 had 135. One needs to adjust for this difference across districts in the pre-treatment period. To analyze the Mississippi experiment, we leverage a tool called **difference-in-differences**

.footnote[<sup>1</sup>Gary Richardson and William Troost, “Monetary Intervention Mitigated Banking Panics during the Great Depression: Quasi-Experimental Evidence from a Federal Reserve District
Border, 1929–1933,” *Journal of Political Economy*, December 2009.]

---

# Monetary Policy and Bank Failures II

* The difference-in-differences estimate `$\delta_{DD}$` of the effect of easy money in the Sixth District is

`$$\delta_{DD}=(Y_{6d, 1931}-Y_{6d,1930})-(Y_{8d,1931}-Y_{8d,1930})=\\
(121-135)-(132-165)=19$$`

* Instead of comparing the number of banks open in the `$6^{th}$` and `$8^{th}$` district, DinD contrasts the change in the number of banks operating in the two districts

* DinD estimates suggests that the Atlanta Fed saved 19 banks in 1931 with an easy money policy

]

.pull-right[
<table class=" lightable-paper table" style='font-family: "Arial Narrow", arial, helvetica, sans-serif; width: auto !important; margin-left: auto; margin-right: auto; margin-left: auto; margin-right: auto;'>
<caption>2x2 Difference-in-Differences</caption>
 <thead>
<tr>
<th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="1"><div style="">District</div></th>
<th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="">Number of Banks Operating</div></th>
<th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="1"><div style="">Difference</div></th>
</tr>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:left;"> 1930 </th>
   <th style="text-align:left;"> 1931 </th>
   <th style="text-align:left;"> 1931-1930 </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> District 6 (Treatment Group) </td>
   <td style="text-align:left;"> 135 </td>
   <td style="text-align:left;"> 121 </td>
   <td style="text-align:left;"> -14 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> District 8 (Control Group) </td>
   <td style="text-align:left;"> 165 </td>
   <td style="text-align:left;"> 132 </td>
   <td style="text-align:left;"> -33 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Difference </td>
   <td style="text-align:left;"> 30 </td>
   <td style="text-align:left;"> 11 </td>
   <td style="text-align:left;"> 19 </td>
  </tr>
</tbody>
</table>
.small[**Source: Angrist and Pischke (2014).**]
]

---
#  Parallel Trends I

* The DinD logic of trend comparison is depicted in the figure. While banks failed in both Districts, in the Eighth District that was much more pronounced

* The dashed line represents the counterfactual outcome - what would have happened in the Sixth District had everything evolved as it did in the Eighth District. The solid line declines much more gradually than the counterfactual, showing that the easy money policy effectively kept banks in business

* The 19 banks uncovered by the DinD estimates is the difference between what really happened and what would have happened had bank activity in the two Districts unfolded in parallel

]

.pull-right[
![](figs/plot1.png)
.small[**This figure shows the number of banks in operation in Mississippi in the Sixth and
Eighth Federal Reserve Districts in 1930 and 1931. The dashed line depicts the counterfactual
evolution in the Sixth District if the same number of banks had failed in
that district in this period as did in the Eighth. Source: Angrist and Pischke (2014).**]

]

---

# Parallel Trends II

* The main identification assumption is that, in the absence of easy money, the number of banks operating in Districts `$6^{th}$` and `$8^{th}$` would have evolved in a parallel fashion - that is what we call *common trends assumption*.

* The figure provides information about bank activity from 1929 to 1934. The fact that bank failures moved almost in parallel in the two Districts between 1929 and 1930 is consistent with the common trends assumption

* Also, after 1931, the St. Louis Fed started adopting an easy money policy, making Districts `$6^{th}$` and `$8^{th}$` similar again. Although the Great Depression was far from over in 1932, the cash withdrawals were back to normal levels. Given the two regional Feds' same willingness to lend money to banks in need, bank activity in both districts should have common trends again. And that is what we see in the data

]

![](figs/plot2.png)
.small[**The dashed line depicts the counterfactual evolution of the number of banks in the Sixth Districtif the same number of banks had failed in that district after 1930 as did in the Eighth. Source: Angrist and Pischke (2014).**]
]

---

# Easy Money and Economic Activity

* The Atlanta Fed might have saved many banks in the Sixth District part of Mississippi. Did Atlanta Fed's policy of easy money support real economic activity?

* The table shows DinD analysis of Federal Reserve liquidity effects on the number of active wholesalers and their sales (in $ million)
  
  * The results suggest that the reduction in bank credit in the Eighth District in the wake of Caldwell brought wholesale business activity down as well

* Overall, after the crisis, the Sixth District's economic contraction slowed, and recovery began. In the Eighth District, lending declined, business faltered, and unemployment rose

]

![](figs/table.png)
.small[**This table presents a DinD analysis of Federal Reserve liquidity effects on the number of
wholesale firms and the dollar value of their sales, paralleling the DinD analysis of liquidity effects on bank activity from before. Source: Angrist and Pischke (2014)**]
]

---

---
<style type="text/css">
.pull-left3 {
  float: left;
  width: 59%;
}
.pull-right3 {
  float: right;
  width: 40%;
}
.pull-right3 ~ p {
  clear: both;
}
</style>

# John Snow (1813-1858)

* John Snow was an English physician and a leader in the development of anesthesia and medical hygiene

* He had long believed that cholera was spread by contaminated water, but the dominant theory was that cholera was transmitted by breathing "bad air"
   
  * Cholera is an intestinal illness that can cause death within hours after the first symptoms, and the first cases of the disease in London were recorded in 1831 
  
  * London suffered with multiple waves of Cholera, and John Snow worked there during theses epidemics

* Before develop a theory about cholera transmission, he gathered multiple anecdotal evidence to rule out *miasma*

* He is considered the father of modern epidemiology

]

---

# The Broad Street Pump

* By the 1800s, most people did not have running water and basic sanitation in their houses and used communal pumps to get the water for cooking, drinking, and washing

* Snow published an article in 1849 outlining his theory about the mechanism behind cholera transmission, but he could not convince other doctors and scientists

* In August of 1854, Soho - a suburb of London - was hit hard by an outbreak of cholera. Living near Soho, Dr. Snow could do some fieldwork to prove his theory

* [“Within 250 yards of the spot where Cambridge Street joins Broad Street there were upwards of 500 fatal attacks of cholera in 10 days,” Dr. Snow wrote  “As soon as I became acquainted with the situation and extent of this irruption (sic) of cholera, I suspected some contamination of the water of the much-frequented street-pump in Broad Street.”](https://www.ph.ucla.edu/epi/snow/snowcricketarticle.html)

]

![](figs/pump.png)
]

---
# John Snow Mapping Cholera Deaths I

* Snow used a geographical grid to chart deaths from the outbreak, and the dot map would illustrate the cluster of cholera cases very close to the water pump

* He also investigated cases to determine whether they were related to the same pump in Broad Street

* Together with his empirical findings, Dr. Snow also had anecdotal evidence coming from many different sources

* For instance, a brewery located on Broad Street. Among its 70 workers, there were no fatalities. The explanation is that the men were given an allowance of free beer every day and so never drank water at all

]
.pull-right[![](figs/SnowMap.png)]

---
# John Snow Mapping Cholera Deaths II

---

# John Snow Getting Causal Effects I

* The most compelling evidence that Cholera was transmitted by contaminated water came from a "natural experiment." At that time, different companies were responsible for the water distribution within London, often bottling water from the Thames

* In 1849, Lambeth company decided to move their pipes higher up (above the main sewage discharge point) in the Thames river to get cleaner water, while Southwark and Vauxhall did not

* If Snow's theory about cholera transmission was correct, households served by Lambeth would have lower cholera rates. He linked household enrollment in water supply companies with cases of Cholera and made his case for the cause of cholera transmission

* While Snow did not explicitly estimate treatment effects through difference-in-differences, the intuition was there

]

]

---

# What is behind DiD? I

* Assume the intervention `$D$` is clean water, and the goal is to estimate the causal effect of that on cholera deaths. What do we get comparing cholera deaths between Lambeth and Southwark and Vauxhall companies? (i.e., cross-sectional comparison)

* Without randomization, the naive comparison is full of selection bias. Say `$L$` and `$SV$` are something unique about those companies that are not observed and also do not change over time. The naive comparison leads to the following difference:

`$$\underbrace{D}_{\text{Causal effect of interest}}+\underbrace{(L-SV)}_{\text{Selection bias}}$$`

]

]
---

# What is behind DiD? II

* When we compare Lambeth households' cholera rates before and after the company moved their pipes higher up the Thames River, we get:

`$$L+(T+D)-L=\\
\underbrace{D}_{\text{Causal effect of interest}}+\underbrace{T}_{\text{Natural changes over time}}$$`
* Although the before and after difference eliminates the Lambeth fixed effects, you still have bias related to natural changes in the cholera deaths over time

]

]
---

# What is behind DiD? III

* The intuition of the DiD strategy is to combine two differences and get rid of selection bias and time effects

* The first difference is the before-and-after comparison for each company. Hence, you eliminate unit-specific fixed effects. After calculating the within differences, we subtract these two differences to eliminate time effects and get an unbiased estimate of the causal effect of interest `$D$`

* As you can imagine, we assume that there are no time-variant company-specific unobservables. `$T$` is the same for all units, and that is the *common trends* assumption we discussed before

]

<table class=" lightable-paper table" style='font-family: "Arial Narrow", arial, helvetica, sans-serif; width: auto !important; margin-left: auto; margin-right: auto; font-size: 20px; margin-left: auto; margin-right: auto;'>
 <thead>
  <tr>
   <th style="text-align:left;"> Company </th>
   <th style="text-align:left;"> Time </th>
   <th style="text-align:left;"> Outcome </th>
   <th style="text-align:left;"> First.Diff. </th>
   <th style="text-align:left;"> Second.Diff. </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> Lambeth </td>
   <td style="text-align:left;"> Before </td>
   <td style="text-align:left;"> Y=L </td>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;"> After </td>
   <td style="text-align:left;"> Y=L+(T+D) </td>
   <td style="text-align:left;"> T+D </td>
   <td style="text-align:left;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;"> D </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Southwark and Vauxhall </td>
   <td style="text-align:left;"> Before </td>
   <td style="text-align:left;"> Y=SV </td>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;">  </td>
   <td style="text-align:left;"> After </td>
   <td style="text-align:left;"> Y=SV+T </td>
   <td style="text-align:left;"> T </td>
   <td style="text-align:left;">  </td>
  </tr>
</tbody>
<tfoot>
<tr>
<td style = 'padding: 0; border:0;' colspan='100%'><sup></sup> Source: Cunningham (2021). Difference in each company's differences</td>
</tr>
</tfoot>
</table>

.small[**Note: leveraging natural experiments and using repeated observations of treatment and control units, we eliminate the unobserved heterogeneity to estimate causal effects.**]
]

---
class: inverse, middle, center
# DiD regression estimates

---
# Back to the Mississippi Experiment

To cook the DiD recipe with regression models, you will need:

1. A dummy for the treatment units `$TREAT_{i}$`, which controls for fixed differences between units being compared

2. A dummy that identifies post-treatment periods `$POST_{t}$`, which controls for the fact that conditions change over time for everyone

3. The interaction term `$Dint$` - just multiply `$TREAT_{i}$` by `$POST_{t}$`. The coefficient on `$Dint$` identifies the causal effect of interest
 
You end up estimating

`$$Y_{it}=\alpha+\beta Dint_{it} + \lambda POST_{t} + \gamma TREAT_{i}+\varepsilon_{it}$$`

]

```r
options(scipen=999)
banks<-readRDS("banks.RDS")
library(reshape2)
panel_banks<-melt(banks, id.var='year')
panel_banks$TREAT<-ifelse(panel_banks$variable=="6th district",1,0)
panel_banks$POST<-ifelse(panel_banks$year>=1931,1,0)
panel_banks$Dint<-panel_banks$TREAT*panel_banks$POST

dind_reg1<-lm(value~Dint+TREAT+POST, data=panel_banks)

library(stargazer)
stargazer(dind_reg1, header = F, single.row = TRUE, no.space = T, dep.var.labels.include = FALSE,dep.var.caption = "Number of Banks operating", type='html', omit.stat=c("rsq", "ser", "f"))
```

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Number of Banks operating</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Dint</td><td>20.500<sup>*</sup> (10.721)</td></tr>
<tr><td style="text-align:left">TREAT</td><td>-29.000<sup>**</sup> (8.754)</td></tr>
<tr><td style="text-align:left">POST</td><td>-49.000<sup>***</sup> (7.581)</td></tr>
<tr><td style="text-align:left">Constant</td><td>167.000<sup>***</sup> (6.190)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>12</td></tr>
<tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td>0.850</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
</table>

]

```r
library(fixest)
dind_reg2<-feols(value~Dint|variable+year, se="standard", data=panel_banks)
summary(dind_reg2)
```

]

```
##                        dind_reg2
## Dependent Var.:            value
##                                 
## Dint            20.50*** (1.561)
## Fixed-Effects:  ----------------
## variable                     Yes
## year                         Yes
## _______________ ________________
## S.E. type                    IID
## Observations                  12
## R2                       0.99884
## Within R2                0.97733
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

---
class: inverse, middle, center
# Example: Minimum Legal Drinking Age (MLDA)

---
# MLDA in U.S. States

* Because of state federalism, each U.S. state has enough discretion to set and/or change its own policies. This frequent policy variation in state laws makes the U.S. a laboratory for those interested in causal inference. For example, **let's take a look at the state MLDA laws:**

* The U.S. states were free to regulate alcohol consumption in 1933, after the repeal of the Federal prohibition. Most states instituted an MLDA of 21, but some allowed drinking at 18 (New York, Kansas, and North Carolina)
  
  * By the time of the Vietnam War, many states lowered the MLDA to 18 following the process that lowered the voting age to 18. Arkansas, California, and Pennsylvania did not follow the pattern and kept the MLDA at 21

]

.pull-right[
![](figs/cdc.png)
.small[**Source: [CDC website](https://www.cdc.gov/alcohol/fact-sheets/minimum-legal-drinking-age.htm).**]

]

---

# MLDA Experiment: 2x2

**These variations in MLDA laws can be exploited in a DiD framework**. For instance, Alabama lowered its MLDA to 19 in 1975, but Arkansas kept an MLDA of 21 since Prohibition's repeal. Did Alabama's indulgence of its youthful drinkers cost some of them their lives?

One can fit a regression DiD model to data on death rates of 18-20-year-olds from 1970 to 1983:

`$$Y_{st}=\alpha+\beta Dint_{st} + \lambda POST_{t} + \gamma TREAT_{s}+\varepsilon_{st}$$`
where `$TREAT_{s}$` is a dummy indicating Alabama, `$POST_{t}$` is a dummy indicating years from 1975 to 1983, and `$Dint_{st}$` is the interaction term for Alabama observations from low-drinking-age years.

]

<div style="border: 1px solid #ddd; padding: 0px; overflow-y: scroll; height:450px; overflow-x: scroll; width:100%; "><table class="table table-striped table-condensed" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> year </th>
   <th style="text-align:left;position: sticky; top:0; background-color: #FFFFFF;"> Statename </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> mrate </th>
   <th style="text-align:left;position: sticky; top:0; background-color: #FFFFFF;"> agegr </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> treat </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> post </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> Dint </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> legal </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 1970 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 153.87047 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1971 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 161.53520 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1972 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 159.21349 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1973 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 140.88599 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1974 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 143.09831 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1975 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 147.94107 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.2939954 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1976 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 132.60246 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6650701 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1977 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 145.82703 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6684675 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1978 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 138.74785 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6671846 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1979 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 135.41170 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6680924 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1980 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 120.10757 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6722586 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1981 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 105.87334 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6792082 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1982 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 118.30740 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6759089 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1983 </td>
   <td style="text-align:left;"> Alabama </td>
   <td style="text-align:right;"> 128.15288 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.6796314 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1970 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 167.96689 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1971 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 162.70203 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1972 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 194.77879 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1973 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 167.58173 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1974 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 119.61935 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1975 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 148.94630 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1976 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 137.48776 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1977 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 111.52692 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1978 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 141.57468 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1979 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 136.38689 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1980 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 137.51550 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1981 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 95.88255 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1982 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 122.50186 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 1983 </td>
   <td style="text-align:left;"> Arkansas </td>
   <td style="text-align:right;"> 110.20988 </td>
   <td style="text-align:left;"> 18-20 yrs </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 0.0000000 </td>
  </tr>
</tbody>
</table></div>

]

---

# MLDA Experiment: 2x2 Results

The 2x2 DiD can be tabulated in the following way:

According to the difference-in-differences estimate, deaths per 100,000 people increased by 14 due to the new MLDA policy in Alabama.

]

.pull-right2[
Download the data [here](https://github.com/guerramarcelino/PolicyEval/raw/main/Datasets/sub_mlda.RDS).

```r
library(tidyverse)
data<-readRDS("sub_mlda.RDS")
before_AL<-data%>%filter(Statename=="Alabama", year<1975)%>%summarize(mrate=mean(mrate))
before_AL

after_AL<-data%>%filter(Statename=="Alabama", year>=1975)%>%summarize(mrate=mean(mrate))
after_AL

before_AK<-data%>%filter(Statename=="Arkansas", year<1975)%>%summarize(mrate=mean(mrate))
before_AK

after_AK<-data%>%filter(Statename=="Arkansas", year>=1975)%>%summarize(mrate=mean(mrate))
after_AK
```

]

```r
data$treat<-ifelse(data$Statename=="Alabama", 1, 0)
data$post<-ifelse(data$year>=1975,1,0)
data$Dint<-data$treat*data$post

library(fixest)
reg<-feols(mrate~Dint|Statename+year, se="hetero",data=data)
etable(reg)
```

]

```
##                           reg
## Dependent Var.:         mrate
##                              
## Dint            14.25 (11.26)
## Fixed-Effects:  -------------
## Statename                 Yes
## year                      Yes
## _______________ _____________
## S.E. type       Heteros.-rob.
## Observations               28
## R2                    0.84499
## Within R2             0.14050
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

```r
library(ggthemes)
plot<-ggplot()+
 geom_line(data=data, 
           aes(x=year, y=mrate, col=Statename),
           size=1.4)+
 scale_color_fivethirtyeight("State")+
 theme_fivethirtyeight()+
 labs(x = "Year", y="Mortality Rate")+
 geom_vline(xintercept = 1975, linetype="dashed")+
 theme(axis.text=element_text(size=12),
        axis.title=element_text(size=12,face="bold"))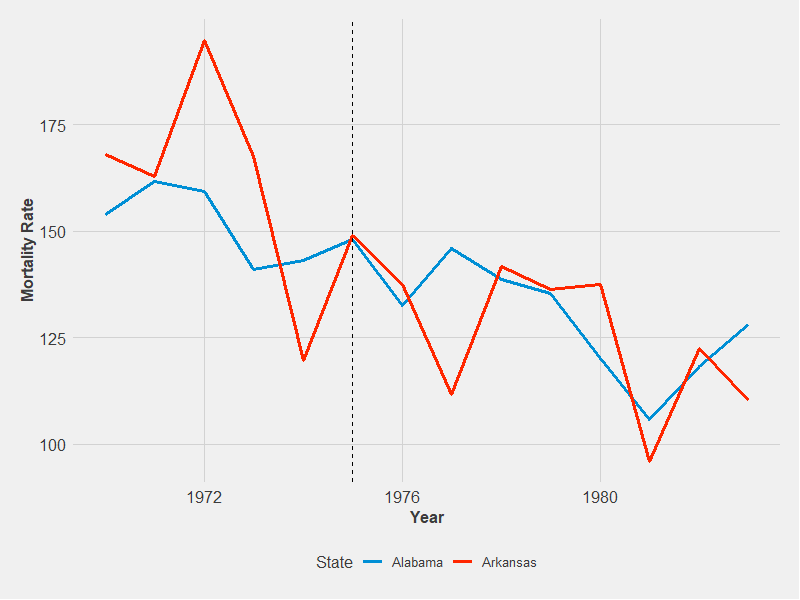
```

]

![](figs/mlda.png)

]

---

# MLDA Experiment: Multistate Regression

* There is more than Alabama *vs.* Arkansas in the MDLA experiment. For instance, Tennessee's MLDA fell to 18 in 1971, then rose to 19 in 1979. One can combine all states and explore the differences in the timing of MLDA reductions

* When combining multiple MLDA experiments in a DiD framework, you need to add *state* and *time* fixed effects
  
  * *time* fixed effects will capture temporal changes in death rates that are common to all states
  * *state* fixed effects control for unobserved characteristics that are fixed over time for each state
  * *time* FE replaces `$POST_{t}$`, and *state* FE replaces `$TREAT_{s}$` in the DiD regression

* In the MLDA experiment, we also simplify the `$Dint_{st}$` variable, replacing it with a measure of access to alcohol called `$LEGAL_{st}$` - a variable that measures the proportion of 18-20-years-olds allowed to drink in state `$s$` and year `$t$`.

* The multistate regression DD model looks like

`$$Y_{st}=\alpha+\beta LEGAL_{st}+\lambda_{t}+\gamma_{s}+\varepsilon_{st}$$`
where `$\gamma_{s}$` is a set of state dummies (state FE) and `$\lambda_{t}$` a set of time dummies (time FE).

---

# MLDA Experiment: Multistate Regression Results

* The multistate MLDA analysis uses 14 years and 51 states. The estimated coefficient on `$LEGAL_{st}$` suggests that legal alcohol access caused around 11 additional deaths per 100,000 18-20 year-olds, of which seven on eight deaths were the result of motor vehicle accidents

]
.pull-right[

```
##                           reg1            reg2
## Dependent Var.:          mrate           mrate
##                                               
## legal           10.80* (4.425) 7.592** (2.405)
## Fixed-Effects:  -------------- ---------------
## state                      Yes             Yes
## year                       Yes             Yes
## _______________ ______________ _______________
## S.E.: Clustered      by: state       by: state
## Observations               714             714
## R2                     0.82116         0.79766
## Within R2              0.01794         0.02208
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

Download the data [here](https://github.com/guerramarcelino/PolicyEval/raw/main/Datasets/mlda.RDS).

```r
mlda<-readRDS("mlda.RDS")
## All deaths 18-20 year olds/period 1970-1983
all_deaths<-mlda%>%filter(dtype=="all", agegr=="18-20 yrs", year<=1983)
reg1<-feols(mrate~legal|state+year,cluster=~state, data=all_deaths)
## Deaths due to motor vehicle accidents 18-20 year olds/period 1970-1983
mv_deaths<-mlda%>%filter(dtype=="MVA", agegr=="18-20 yrs", year<=1983)
reg2<-feols(mrate~legal|state+year,cluster=~state, data=mv_deaths)

etable(reg1, reg2,signifCode = c("***"=0.01, "**"=0.05, "*"=0.10))
```

]

---

# MLDA Experiment: Multistate Regression Robustness I

* When using DiD, your main identification assumption is parallel trends: in the absence of new MLDA laws that allow people under 21 to drink, death rates among 18-20-year-olds in the treated and control states would have evolved in a parallel fashion

* Samples that have many states and years allow us to relax the common trends assumption. One can introduce state-specific time trends using the following model:

`$$Y_{st}=\alpha+\beta LEGAL_{st}+\lambda_{t}+\gamma_{s}+\tau_{st}+\varepsilon_{st}$$`
where `$\tau_{st}$` represents specific state trends. This model presumes that in the absence of a treatment effect, death rates in states deviate from common year effects by following the linear trend captured by the coefficients on `$\tau_{st}$`.

]

* Models with state-specific linear trends provide a robustness check on the causal interpretation of any set of DiD regression estimates using multiperiod data. In the MLDA analysis, the introduction of state-specific time trends has some effect on the DiD estimates, but the results still hold

]
.pull-right[

```
##                           reg3           reg4
## Dependent Var.:          mrate          mrate
##                                              
## legal           8.467. (4.898) 6.644* (2.552)
## Fixed-Effects:  -------------- --------------
## state                      Yes            Yes
## year                       Yes            Yes
## _______________ ______________ ______________
## S.E.: Clustered      by: state      by: state
## Observations               714            714
## R2                     0.84843        0.83606
## Within R2              0.16768        0.20769
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

```r
## All deaths 18-20 year olds/period 1970-1983

all_deaths<-mlda%>%filter(dtype=="all", agegr=="18-20 yrs", year<=1983)
reg3<-feols(mrate~legal+state:year|state+year, data=all_deaths)
## Deaths due to motor vehicle accidents 18-20 year olds/period 1970-1983
mv_deaths<-mlda%>%filter(dtype=="MVA", agegr=="18-20 yrs", year<=1983)
reg4<-feols(mrate~legal+state:year|state+year,cluster=~state, data=mv_deaths)

etable(reg3, reg4,signifCode = c("***"=0.01, "**"=0.05, "*"=0.10))
```

]

---

# MLDA Experiment: Multistate Regression Robustness II

* Sometimes, contemporaneous policy changes in other areas confound the treatment effect that you are trying to estimate. For instance, an important variable to consider in the MLDA experiment is the price of a drink - and taxes are most likely affecting that price

* Think about the following scenario: states increase both the MLDA and the tax on beer in a broader effort to reduce alcohol consumption. Hence, you can expect both policies to bring alcohol consumption down and affect mortality rates of 18-to 20-year-olds

* To deal with that potential threat, you can include controls for state beer taxes:

`$$Y_{st}=\alpha+\beta LEGAL_{st}+\theta BeerTax_{st}+\lambda_{t}+\gamma_{s}+\tau_{st}+\varepsilon_{st}$$`

]

* The MLDA estimates with and without `$BeerTax_{st}$` are very similar - the estimated coefficients are not precise, most likely because beer taxes change less often than MLDA laws

]
.pull-right[

```
##                           reg5            reg6
## Dependent Var.:          mrate           mrate
##                                               
## legal           10.03* (4.722) 6.888** (2.559)
## beertaxa        -5.525 (30.98)   26.88 (19.33)
## Fixed-Effects:  -------------- ---------------
## state                      Yes             Yes
## year                       Yes             Yes
## _______________ ______________ _______________
## S.E.: Clustered      by: state       by: state
## Observations               700             700
## R2                     0.85029         0.83595
## Within R2              0.16240         0.20951
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

```r
## All deaths 18-20 year olds/period 1970-1983

all_deaths<-mlda%>%filter(dtype=="all", agegr=="18-20 yrs", year<=1983)
reg5<-feols(mrate~legal+beertaxa+state:year|state+year,cluster=~state, data=all_deaths)
## Deaths due to motor vehicle accidents 18-20 year olds/period 1970-1983
mv_deaths<-mlda%>%filter(dtype=="MVA", agegr=="18-20 yrs", year<=1983)
reg6<-feols(mrate~legal+beertaxa+state:year|state+year,cluster=~state, data=mv_deaths)

etable(reg5, reg6,signifCode = c("***"=0.01, "**"=0.05, "*"=0.10), drop=c("state[[:digit:]]{1}","state[[:digit:]]{2}"))
```

]

---

class: inverse, middle, center
# Does Strengthening Self-Defense Law Deter Crime or Escalate Violence? Evidence from Expansions to Castle Doctrine

---

# Castle-doctrine Statutes

* In 2005, a wave of states (starting with Florida) began passing "stand your ground" laws<sup>1</sup>

* A long-standing principle of English common law is that you have a "duty to retreat" before using lethal force against an assaulter - the exception is when the assault occurs at your home (your "castle") 
  
  * From 2005 to 2010, twenty-one U.S. states extended Castle Doctrine to places outside the home such as one's vehicle, place of work, and in some cases, any place one has a legal right to be
  
  * These new laws also granted immunity from civil liability when using justified defensive force
  
  * Some laws added a presumption of reasonable fear of imminent serious injury or death, which shifts the burden of proof to the prosecutor to show someone acted unreasonably

.footnote[
[1] Cheng Cheng and Mark Hoekstra, "Does Strengthening Self-Defense Law Deter Crime or Escalate Violence? Evidence from Expansions to Castle Doctrine," *The Journal of Human Resources*, 2013.]

---
# Castle-doctrine Expansion

---
# Castle-doctrine, Deterrence, and Homicides

* The primary rationale for these "stand your ground" laws were to provide additional legal leeway to potential victims in a self-defense situation, but one can expect these versions of Castle-doctrine to alter incentives in important ways
  
  * Under these new laws, the expected cost of using lethal force is diminished - there is a lower probability that one is found guilt for death/injury inflicted
  
  * The laws increase the expected cost of committing a violent crime - victims are more likely to respond to threats by using lethal force
  
* Ultimately, whether or not people respond to these changes is an empirical question. It is also important to estimate the costs and benefits of the law. To assess these possibilities, Cheng and Hoekstra (2013) evaluate the impact of the Castle-doctrine on

1. Motor theft and larceny (*falsification exercise*)

2. Burglary, robbery, and aggravated assault (*crime deterrence*)

3. Homicides (*violence escalation*)

---
# Identification

The research design is difference-in-differences: the study exploits the staggered adoption of Castle-doctrine laws between 2000 and 2010. The sample comprehends 50 U.S. states (21 eventually treated) and 11 years. The estimation method is two-way fixed effects:

`$$\text{Log(Crime rate)}_{it}=\beta CDL_{it} + X^{'}_{it}\theta + \lambda_{t} + \mu_{i}+\tau_{rt} +\varepsilon_{it}$$`
where different types of crimes are considered as outcomes, `$CDL_{it}$` is the treatment variable that equals the proportion of year `$t$` in which state `$i$` has an effective Castle-doctrine law, `$X_{it}$` is a vector of time-varying control variables, `$\lambda_{t}$` is year fixed effects, `$\mu_{i}$` is state fixed effects, `$\tau_{rt}$` is region-by-year fixed effects, and `$\varepsilon_{it}$` is the error term.

**The identifying assumption** is the following: in the absence of the Castle-doctrine laws, adopting states would have experienced changes in crime similar to nonadopting states in the same region of the country. To assess whether the common trends assumption is reasonable, one can look for visual evidence.

---
# Main results

* No effect of Castle-doctrine on robbery. Same for aggravated assault and burglary

* Those results indicate that the law did not have any deterrent effect

]

```
##                        reg_rob1        reg_rob2         reg_rob3
## Dependent Var.:       l_robbery       l_robbery        l_robbery
##                                                                 
## cdl             0.0408 (0.0254) 0.0344 (0.0227) 0.0515. (0.0279)
## Fixed-Effects:  --------------- --------------- ----------------
## state                       Yes             Yes              Yes
## year                        Yes             Yes              Yes
## region-year                  No             Yes              Yes
## _______________ _______________ _______________ ________________
## S.E.: Clustered       by: state       by: state        by: state
## Observations                550             550              550
## R2                      0.97832         0.98099          0.98964
## Within R2               0.01899         0.00993          0.46041
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

.small[**Note: The first column only considers state and year FEs. The second column adds region-by-year fixed effects, and the third column adds time-varying covariates and state-specific trends. All regressions are weighted by state population. Full replication exercise [here](https://guerramarcelino.github.io/Econ474/Rlabs/lab8#difference-in-differences-example-cheng-and-hoekstra-2013).**]
]
]

* The Castle-doctrine law increased murder by 8% - results are significant at 5% level when using population-weighted regression

* This accounts for 600 additional murders per year across the 21 states where the law was implemented

]

```
##                       reg_homic1        reg_homic2       reg_homic3
## Dependent Var.:       l_homicide        l_homicide       l_homicide
##                                                                    
## cdl             0.0801* (0.0342) 0.0946** (0.0282) 0.1004* (0.0395)
## Fixed-Effects:  ---------------- ----------------- ----------------
## state                        Yes               Yes              Yes
## year                         Yes               Yes              Yes
## region-year                   No               Yes              Yes
## _______________ ________________ _________________ ________________
## S.E.: Clustered        by: state         by: state        by: state
## Observations                 550               550              550
## R2                       0.93417           0.94109          0.96239
## Within R2                0.03018           0.03020          0.38079
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]