Econ 474 - Econometrics of Policy Evaluation

# Econ 474 - Econometrics of Policy Evaluation
## Regression
### Marcelino Guerra
### February 02-07, 2022

---

# Describing Relationships

* For most research questions, we are interested in the relationship between two (or more) variables, i.e., what learning about one variable tells us about the other

* Consider the classic example of **salary** and **years of education**. The scatterplot shows the relationship between those two variables: we would like to explain the variation in hourly wages with education levels

* It seems that there is a positive relationship between salary and education

]

<div id="htmlwidget-724fe470d31ac94b1ecb" style="width:560px;height:430px;" class="plotly html-widget"></div>
<script type="application/json" data-for="htmlwidget-724fe470d31ac94b1ecb">{"x":{"data":[{"x":[11,12,11,8,12,16,18,12,12,17,16,13,12,12,12,16,12,13,12,12,12,12,16,12,11,16,16,16,15,8,14,14,13,12,12,16,12,4,14,12,12,12,14,11,13,15,10,12,14,12,12,16,12,12,12,15,16,8,18,16,13,14,10,10,14,14,16,12,16,12,16,17,12,12,12,13,12,12,12,18,9,16,10,12,12,12,12,12,8,12,12,14,12,12,12,9,13,12,14,12,15,12,12,12,14,15,12,12,12,17,11,18,12,14,14,10,14,12,15,8,16,14,15,12,18,16,10,8,10,11,18,15,12,11,12,12,14,16,2,14,16,12,12,13,12,15,10,12,16,13,9,12,13,12,12,14,16,16,9,18,10,10,13,12,18,13,12,13,13,13,18,12,12,13,12,12,12,14,10,12,16,16,12,14,12,12,12,12,12,12,12,16,16,14,11,16,12,12,17,12,12,16,8,12,12,12,16,12,12,9,13,16,14,8,14,13,12,18,9,8,8,12,14,12,16,8,13,9,16,12,15,11,14,12,12,12,18,12,12,12,12,12,12,14,16,12,14,11,12,10,12,6,13,12,10,12,14,13,12,18,12,12,12,12,12,8,13,13,14,12,10,16,12,16,12,14,18,17,13,14,15,14,12,8,12,12,8,12,9,12,16,12,16,12,12,13,10,6,12,12,16,12,8,12,6,4,11,11,7,12,18,12,16,12,14,12,10,10,9,10,12,12,12,10,16,16,16,12,12,7,8,16,16,18,13,10,16,14,16,12,9,11,11,12,11,12,12,12,12,14,14,18,12,12,12,11,12,17,16,13,13,12,14,14,11,10,8,14,12,10,17,9,12,12,14,16,12,10,0,14,15,16,12,11,11,12,13,12,13,16,15,16,15,12,18,6,6,12,12,16,9,12,11,10,12,8,9,17,16,11,10,8,13,14,13,11,7,16,12,13,14,16,14,11,8,14,17,10,12,12,18,14,18,12,16,14,12,9,12,12,17,12,15,17,16,12,15,16,12,15,12,12,12,12,16,11,14,14,13,14,12,12,8,12,3,11,15,11,12,4,9,12,12,11,12,16,13,15,16,12,12,12,9,10,12,11,8,6,16,12,12,16,12,10,13,13,14,16,10,12,12,11,0,5,16,16,9,15,12,12,12,13,12,7,17,12,12,14,12,13,12,16,10,15,16,14],"y":[3.09999990463257,3.24000000953674,3,6,5.30000019073486,8.75,11.25,5,3.59999990463257,18.1800003051758,6.25,8.13000011444092,8.77000045776367,5.5,22.2000007629395,17.3299999237061,7.5,10.6300001144409,3.59999990463257,4.5,6.88000011444092,8.47999954223633,6.32999992370605,0.529999971389771,6,9.5600004196167,7.78000020980835,12.5,12.5,3.25,13,4.5,9.68000030517578,5,4.67999982833862,4.26999998092651,6.15000009536743,3.50999999046326,3,6.25,7.80999994277954,10,4.5,4,6.38000011444092,13.6999998092651,1.66999995708466,2.9300000667572,3.65000009536743,2.90000009536743,1.62999999523163,8.60000038146973,5,6,2.5,3.25,3.40000009536743,10,21.6299991607666,4.38000011444092,11.710000038147,12.3900003433228,6.25,3.71000003814697,7.78000020980835,19.9799995422363,6.25,10,5.71000003814697,2,5.71000003814697,13.0799999237061,4.90999984741211,2.91000008583069,3.75,11.8999996185303,4,3.09999990463257,8.44999980926514,7.1399998664856,4.5,4.65000009536743,2.90000009536743,6.67000007629395,3.5,3.25999999046326,3.25,8,9.85000038146973,7.5,5.90999984741211,11.7600002288818,3,4.80999994277954,6.5,4,3.5,13.1599998474121,4.25,3.5,5.13000011444092,3.75,4.5,7.63000011444092,15,6.84999990463257,13.3299999237061,6.67000007629395,2.52999997138977,9.80000019073486,3.36999988555908,24.9799995422363,5.40000009536743,6.1100001335144,4.19999980926514,3.75,3.5,3.64000010490417,3.79999995231628,3,5,4.63000011444092,3,3.20000004768372,3.91000008583069,6.42999982833862,5.48000001907349,1.5,2.90000009536743,5,8.92000007629395,5,3.51999998092651,2.90000009536743,4.5,2.25,5,10,3.75,10,10.9499998092651,7.90000009536743,4.71999979019165,5.84000015258789,3.82999992370605,3.20000004768372,2,4.5,11.5500001907349,2.14000010490417,2.38000011444092,3.75,5.51999998092651,6.5,3.09999990463257,10,6.63000011444092,10,2.30999994277954,6.88000011444092,2.82999992370605,3.13000011444092,8,4.5,8.64999961853027,2,4.75,6.25,6,15.3800001144409,14.5799999237061,12.5,5.25,2.17000007629395,7.1399998664856,6.21999979019165,9,10,5.76999998092651,4,8.75,6.53000020980835,7.59999990463257,5,5,21.8600006103516,8.64000034332275,3.29999995231628,4.44000005722046,4.55000019073486,3.5,6.25,3.84999990463257,6.17999982833862,2.91000008583069,6.25,6.25,9.05000019073486,10,11.1099996566772,6.88000011444092,8.75,10,3.04999995231628,3,5.80000019073486,4.09999990463257,8,6.15000009536743,2.70000004768372,2.75,3,3,7.3600001335144,7.5,3.5,8.10000038146973,3.75,3.25,5.82999992370605,3.5,3.32999992370605,4,3.5,6.25,2.95000004768372,5.71000003814697,3,22.8600006103516,9,8.32999992370605,3,5.75,6.76000022888184,10,3,3.5,3.25,4,2.92000007629395,3.05999994277954,3.20000004768372,4.75,3,18.1599998474121,3.5,4.1100001335144,1.96000003814697,4.28999996185303,3,6.44999980926514,5.19999980926514,4.5,3.88000011444092,3.45000004768372,10.9099998474121,4.09999990463257,3,5.90000009536743,18,4,3,3.54999995231628,3,8.75,2.90000009536743,6.26000022888184,3.5,4.59999990463257,6,2.89000010490417,5.57999992370605,4,6,4.5,2.92000007629395,4.32999992370605,18.8899993896484,4.28000020980835,4.57000017166138,6.25,2.95000004768372,8.75,8.5,3.75,3.15000009536743,5,6.46000003814697,2,4.78999996185303,5.78000020980835,3.1800000667572,4.67999982833862,4.09999990463257,2.91000008583069,6,3.59999990463257,3.95000004768372,7,3,6.07999992370605,8.63000011444092,3,3.75,2.90000009536743,3,6.25,3.5,3,3.24000000953674,8.02000045776367,3.32999992370605,5.25,6.25,3.5,2.95000004768372,3,4.69000005722046,3.73000001907349,4,4,2.90000009536743,3.04999995231628,5.05000019073486,13.9499998092651,18.1599998474121,6.25,5.25,4.78999996185303,3.34999990463257,3,8.43000030517578,5.69999980926514,11.9799995422363,3.5,4.23999977111816,7,6,12.2200002670288,4.5,3,2.90000009536743,15,4,5.25,4,3.29999995231628,5.05000019073486,3.57999992370605,5,4.57000017166138,12.5,3.45000004768372,4.63000011444092,10,2.92000007629395,4.51000022888184,6.5,7.5,3.53999996185303,4.19999980926514,3.50999999046326,4.5,3.34999990463257,2.91000008583069,5.25,4.05000019073486,3.75,3.40000009536743,3,6.28999996185303,2.53999996185303,4.5,3.13000011444092,6.3600001335144,4.67999982833862,6.80000019073486,8.52999973297119,4.17000007629395,3.75,11.1000003814697,3.25999999046326,9.13000011444092,4.5,3,8.75,4.1399998664856,2.86999988555908,3.34999990463257,6.07999992370605,3,4.19999980926514,5.59999990463257,10,12.5,3.75999999046326,3.09999990463257,4.28999996185303,10.9200000762939,7.5,4.05000019073486,4.65000009536743,5,2.90000009536743,8,8.43000030517578,2.92000007629395,6.25,6.25,5.1100001335144,4,4.44000005722046,6.88000011444092,5.42999982833862,3,2.90000009536743,6.25,4.34000015258789,3.25,7.26000022888184,6.34999990463257,5.63000011444092,8.75,3.20000004768372,3,3,12.5,2.88000011444092,3.34999990463257,6.5,10.3800001144409,4.5,10,3.80999994277954,8.80000019073486,9.42000007629395,6.32999992370605,4,2.90000009536743,20,11.25,3.5,6,14.3800001144409,6.3600001335144,3.54999995231628,3,4.5,6.63000011444092,9.30000019073486,3,3.25,1.5,5.90000009536743,8,2.90000009536743,3.28999996185303,6.5,4,6,4.07999992370605,3.75,3.04999995231628,3.5,2.92000007629395,4.5,3.34999990463257,5.94999980926514,8,3,5,5.5,2.65000009536743,3,4.5,17.5,8.18000030517578,9.09000015258789,11.8199996948242,3.25,4.5,4.5,3.71000003814697,6.5,2.90000009536743,5.59999990463257,2.23000001907349,5,8.32999992370605,2.90000009536743,6.25,4.55000019073486,3.27999997138977,2.29999995231628,3.29999995231628,3.15000009536743,12.5,5.15000009536743,3.13000011444092,7.25,2.90000009536743,1.75,2.89000010490417,2.90000009536743,17.7099990844727,6.25,2.59999990463257,6.63000011444092,3.5,6.5,3,4.38000011444092,10,4.94999980926514,9,1.42999994754791,3.07999992370605,9.32999992370605,7.5,4.75,5.65000009536743,15,2.26999998092651,4.67000007629395,11.5600004196167,3.5],"text":["educ: 11 wage: 3.10","educ: 12 wage: 3.24","educ: 11 wage: 3.00","educ: 8 wage: 6.00","educ: 12 wage: 5.30","educ: 16 wage: 8.75","educ: 18 wage: 11.25","educ: 12 wage: 5.00","educ: 12 wage: 3.60","educ: 17 wage: 18.18","educ: 16 wage: 6.25","educ: 13 wage: 8.13","educ: 12 wage: 8.77","educ: 12 wage: 5.50","educ: 12 wage: 22.20","educ: 16 wage: 17.33","educ: 12 wage: 7.50","educ: 13 wage: 10.63","educ: 12 wage: 3.60","educ: 12 wage: 4.50","educ: 12 wage: 6.88","educ: 12 wage: 8.48","educ: 16 wage: 6.33","educ: 12 wage: 0.53","educ: 11 wage: 6.00","educ: 16 wage: 9.56","educ: 16 wage: 7.78","educ: 16 wage: 12.50","educ: 15 wage: 12.50","educ: 8 wage: 3.25","educ: 14 wage: 13.00","educ: 14 wage: 4.50","educ: 13 wage: 9.68","educ: 12 wage: 5.00","educ: 12 wage: 4.68","educ: 16 wage: 4.27","educ: 12 wage: 6.15","educ: 4 wage: 3.51","educ: 14 wage: 3.00","educ: 12 wage: 6.25","educ: 12 wage: 7.81","educ: 12 wage: 10.00","educ: 14 wage: 4.50","educ: 11 wage: 4.00","educ: 13 wage: 6.38","educ: 15 wage: 13.70","educ: 10 wage: 1.67","educ: 12 wage: 2.93","educ: 14 wage: 3.65","educ: 12 wage: 2.90","educ: 12 wage: 1.63","educ: 16 wage: 8.60","educ: 12 wage: 5.00","educ: 12 wage: 6.00","educ: 12 wage: 2.50","educ: 15 wage: 3.25","educ: 16 wage: 3.40","educ: 8 wage: 10.00","educ: 18 wage: 21.63","educ: 16 wage: 4.38","educ: 13 wage: 11.71","educ: 14 wage: 12.39","educ: 10 wage: 6.25","educ: 10 wage: 3.71","educ: 14 wage: 7.78","educ: 14 wage: 19.98","educ: 16 wage: 6.25","educ: 12 wage: 10.00","educ: 16 wage: 5.71","educ: 12 wage: 2.00","educ: 16 wage: 5.71","educ: 17 wage: 13.08","educ: 12 wage: 4.91","educ: 12 wage: 2.91","educ: 12 wage: 3.75","educ: 13 wage: 11.90","educ: 12 wage: 4.00","educ: 12 wage: 3.10","educ: 12 wage: 8.45","educ: 18 wage: 7.14","educ: 9 wage: 4.50","educ: 16 wage: 4.65","educ: 10 wage: 2.90","educ: 12 wage: 6.67","educ: 12 wage: 3.50","educ: 12 wage: 3.26","educ: 12 wage: 3.25","educ: 12 wage: 8.00","educ: 8 wage: 9.85","educ: 12 wage: 7.50","educ: 12 wage: 5.91","educ: 14 wage: 11.76","educ: 12 wage: 3.00","educ: 12 wage: 4.81","educ: 12 wage: 6.50","educ: 9 wage: 4.00","educ: 13 wage: 3.50","educ: 12 wage: 13.16","educ: 14 wage: 4.25","educ: 12 wage: 3.50","educ: 15 wage: 5.13","educ: 12 wage: 3.75","educ: 12 wage: 4.50","educ: 12 wage: 7.63","educ: 14 wage: 15.00","educ: 15 wage: 6.85","educ: 12 wage: 13.33","educ: 12 wage: 6.67","educ: 12 wage: 2.53","educ: 17 wage: 9.80","educ: 11 wage: 3.37","educ: 18 wage: 24.98","educ: 12 wage: 5.40","educ: 14 wage: 6.11","educ: 14 wage: 4.20","educ: 10 wage: 3.75","educ: 14 wage: 3.50","educ: 12 wage: 3.64","educ: 15 wage: 3.80","educ: 8 wage: 3.00","educ: 16 wage: 5.00","educ: 14 wage: 4.63","educ: 15 wage: 3.00","educ: 12 wage: 3.20","educ: 18 wage: 3.91","educ: 16 wage: 6.43","educ: 10 wage: 5.48","educ: 8 wage: 1.50","educ: 10 wage: 2.90","educ: 11 wage: 5.00","educ: 18 wage: 8.92","educ: 15 wage: 5.00","educ: 12 wage: 3.52","educ: 11 wage: 2.90","educ: 12 wage: 4.50","educ: 12 wage: 2.25","educ: 14 wage: 5.00","educ: 16 wage: 10.00","educ: 2 wage: 3.75","educ: 14 wage: 10.00","educ: 16 wage: 10.95","educ: 12 wage: 7.90","educ: 12 wage: 4.72","educ: 13 wage: 5.84","educ: 12 wage: 3.83","educ: 15 wage: 3.20","educ: 10 wage: 2.00","educ: 12 wage: 4.50","educ: 16 wage: 11.55","educ: 13 wage: 2.14","educ: 9 wage: 2.38","educ: 12 wage: 3.75","educ: 13 wage: 5.52","educ: 12 wage: 6.50","educ: 12 wage: 3.10","educ: 14 wage: 10.00","educ: 16 wage: 6.63","educ: 16 wage: 10.00","educ: 9 wage: 2.31","educ: 18 wage: 6.88","educ: 10 wage: 2.83","educ: 10 wage: 3.13","educ: 13 wage: 8.00","educ: 12 wage: 4.50","educ: 18 wage: 8.65","educ: 13 wage: 2.00","educ: 12 wage: 4.75","educ: 13 wage: 6.25","educ: 13 wage: 6.00","educ: 13 wage: 15.38","educ: 18 wage: 14.58","educ: 12 wage: 12.50","educ: 12 wage: 5.25","educ: 13 wage: 2.17","educ: 12 wage: 7.14","educ: 12 wage: 6.22","educ: 12 wage: 9.00","educ: 14 wage: 10.00","educ: 10 wage: 5.77","educ: 12 wage: 4.00","educ: 16 wage: 8.75","educ: 16 wage: 6.53","educ: 12 wage: 7.60","educ: 14 wage: 5.00","educ: 12 wage: 5.00","educ: 12 wage: 21.86","educ: 12 wage: 8.64","educ: 12 wage: 3.30","educ: 12 wage: 4.44","educ: 12 wage: 4.55","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 16 wage: 3.85","educ: 14 wage: 6.18","educ: 11 wage: 2.91","educ: 16 wage: 6.25","educ: 12 wage: 6.25","educ: 12 wage: 9.05","educ: 17 wage: 10.00","educ: 12 wage: 11.11","educ: 12 wage: 6.88","educ: 16 wage: 8.75","educ: 8 wage: 10.00","educ: 12 wage: 3.05","educ: 12 wage: 3.00","educ: 12 wage: 5.80","educ: 16 wage: 4.10","educ: 12 wage: 8.00","educ: 12 wage: 6.15","educ: 9 wage: 2.70","educ: 13 wage: 2.75","educ: 16 wage: 3.00","educ: 14 wage: 3.00","educ: 8 wage: 7.36","educ: 14 wage: 7.50","educ: 13 wage: 3.50","educ: 12 wage: 8.10","educ: 18 wage: 3.75","educ: 9 wage: 3.25","educ: 8 wage: 5.83","educ: 8 wage: 3.50","educ: 12 wage: 3.33","educ: 14 wage: 4.00","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 8 wage: 2.95","educ: 13 wage: 5.71","educ: 9 wage: 3.00","educ: 16 wage: 22.86","educ: 12 wage: 9.00","educ: 15 wage: 8.33","educ: 11 wage: 3.00","educ: 14 wage: 5.75","educ: 12 wage: 6.76","educ: 12 wage: 10.00","educ: 12 wage: 3.00","educ: 18 wage: 3.50","educ: 12 wage: 3.25","educ: 12 wage: 4.00","educ: 12 wage: 2.92","educ: 12 wage: 3.06","educ: 12 wage: 3.20","educ: 12 wage: 4.75","educ: 14 wage: 3.00","educ: 16 wage: 18.16","educ: 12 wage: 3.50","educ: 14 wage: 4.11","educ: 11 wage: 1.96","educ: 12 wage: 4.29","educ: 10 wage: 3.00","educ: 12 wage: 6.45","educ: 6 wage: 5.20","educ: 13 wage: 4.50","educ: 12 wage: 3.88","educ: 10 wage: 3.45","educ: 12 wage: 10.91","educ: 14 wage: 4.10","educ: 13 wage: 3.00","educ: 12 wage: 5.90","educ: 18 wage: 18.00","educ: 12 wage: 4.00","educ: 12 wage: 3.00","educ: 12 wage: 3.55","educ: 12 wage: 3.00","educ: 12 wage: 8.75","educ: 8 wage: 2.90","educ: 13 wage: 6.26","educ: 13 wage: 3.50","educ: 14 wage: 4.60","educ: 12 wage: 6.00","educ: 10 wage: 2.89","educ: 16 wage: 5.58","educ: 12 wage: 4.00","educ: 16 wage: 6.00","educ: 12 wage: 4.50","educ: 14 wage: 2.92","educ: 18 wage: 4.33","educ: 17 wage: 18.89","educ: 13 wage: 4.28","educ: 14 wage: 4.57","educ: 15 wage: 6.25","educ: 14 wage: 2.95","educ: 12 wage: 8.75","educ: 8 wage: 8.50","educ: 12 wage: 3.75","educ: 12 wage: 3.15","educ: 8 wage: 5.00","educ: 12 wage: 6.46","educ: 9 wage: 2.00","educ: 12 wage: 4.79","educ: 16 wage: 5.78","educ: 12 wage: 3.18","educ: 16 wage: 4.68","educ: 12 wage: 4.10","educ: 12 wage: 2.91","educ: 13 wage: 6.00","educ: 10 wage: 3.60","educ: 6 wage: 3.95","educ: 12 wage: 7.00","educ: 12 wage: 3.00","educ: 16 wage: 6.08","educ: 12 wage: 8.63","educ: 8 wage: 3.00","educ: 12 wage: 3.75","educ: 6 wage: 2.90","educ: 4 wage: 3.00","educ: 11 wage: 6.25","educ: 11 wage: 3.50","educ: 7 wage: 3.00","educ: 12 wage: 3.24","educ: 18 wage: 8.02","educ: 12 wage: 3.33","educ: 16 wage: 5.25","educ: 12 wage: 6.25","educ: 14 wage: 3.50","educ: 12 wage: 2.95","educ: 10 wage: 3.00","educ: 10 wage: 4.69","educ: 9 wage: 3.73","educ: 10 wage: 4.00","educ: 12 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 3.05","educ: 10 wage: 5.05","educ: 16 wage: 13.95","educ: 16 wage: 18.16","educ: 16 wage: 6.25","educ: 12 wage: 5.25","educ: 12 wage: 4.79","educ: 7 wage: 3.35","educ: 8 wage: 3.00","educ: 16 wage: 8.43","educ: 16 wage: 5.70","educ: 18 wage: 11.98","educ: 13 wage: 3.50","educ: 10 wage: 4.24","educ: 16 wage: 7.00","educ: 14 wage: 6.00","educ: 16 wage: 12.22","educ: 12 wage: 4.50","educ: 9 wage: 3.00","educ: 11 wage: 2.90","educ: 11 wage: 15.00","educ: 12 wage: 4.00","educ: 11 wage: 5.25","educ: 12 wage: 4.00","educ: 12 wage: 3.30","educ: 12 wage: 5.05","educ: 12 wage: 3.58","educ: 14 wage: 5.00","educ: 14 wage: 4.57","educ: 18 wage: 12.50","educ: 12 wage: 3.45","educ: 12 wage: 4.63","educ: 12 wage: 10.00","educ: 11 wage: 2.92","educ: 12 wage: 4.51","educ: 17 wage: 6.50","educ: 16 wage: 7.50","educ: 13 wage: 3.54","educ: 13 wage: 4.20","educ: 12 wage: 3.51","educ: 14 wage: 4.50","educ: 14 wage: 3.35","educ: 11 wage: 2.91","educ: 10 wage: 5.25","educ: 8 wage: 4.05","educ: 14 wage: 3.75","educ: 12 wage: 3.40","educ: 10 wage: 3.00","educ: 17 wage: 6.29","educ: 9 wage: 2.54","educ: 12 wage: 4.50","educ: 12 wage: 3.13","educ: 14 wage: 6.36","educ: 16 wage: 4.68","educ: 12 wage: 6.80","educ: 10 wage: 8.53","educ: 0 wage: 4.17","educ: 14 wage: 3.75","educ: 15 wage: 11.10","educ: 16 wage: 3.26","educ: 12 wage: 9.13","educ: 11 wage: 4.50","educ: 11 wage: 3.00","educ: 12 wage: 8.75","educ: 13 wage: 4.14","educ: 12 wage: 2.87","educ: 13 wage: 3.35","educ: 16 wage: 6.08","educ: 15 wage: 3.00","educ: 16 wage: 4.20","educ: 15 wage: 5.60","educ: 12 wage: 10.00","educ: 18 wage: 12.50","educ: 6 wage: 3.76","educ: 6 wage: 3.10","educ: 12 wage: 4.29","educ: 12 wage: 10.92","educ: 16 wage: 7.50","educ: 9 wage: 4.05","educ: 12 wage: 4.65","educ: 11 wage: 5.00","educ: 10 wage: 2.90","educ: 12 wage: 8.00","educ: 8 wage: 8.43","educ: 9 wage: 2.92","educ: 17 wage: 6.25","educ: 16 wage: 6.25","educ: 11 wage: 5.11","educ: 10 wage: 4.00","educ: 8 wage: 4.44","educ: 13 wage: 6.88","educ: 14 wage: 5.43","educ: 13 wage: 3.00","educ: 11 wage: 2.90","educ: 7 wage: 6.25","educ: 16 wage: 4.34","educ: 12 wage: 3.25","educ: 13 wage: 7.26","educ: 14 wage: 6.35","educ: 16 wage: 5.63","educ: 14 wage: 8.75","educ: 11 wage: 3.20","educ: 8 wage: 3.00","educ: 14 wage: 3.00","educ: 17 wage: 12.50","educ: 10 wage: 2.88","educ: 12 wage: 3.35","educ: 12 wage: 6.50","educ: 18 wage: 10.38","educ: 14 wage: 4.50","educ: 18 wage: 10.00","educ: 12 wage: 3.81","educ: 16 wage: 8.80","educ: 14 wage: 9.42","educ: 12 wage: 6.33","educ: 9 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 20.00","educ: 17 wage: 11.25","educ: 12 wage: 3.50","educ: 15 wage: 6.00","educ: 17 wage: 14.38","educ: 16 wage: 6.36","educ: 12 wage: 3.55","educ: 15 wage: 3.00","educ: 16 wage: 4.50","educ: 12 wage: 6.63","educ: 15 wage: 9.30","educ: 12 wage: 3.00","educ: 12 wage: 3.25","educ: 12 wage: 1.50","educ: 12 wage: 5.90","educ: 16 wage: 8.00","educ: 11 wage: 2.90","educ: 14 wage: 3.29","educ: 14 wage: 6.50","educ: 13 wage: 4.00","educ: 14 wage: 6.00","educ: 12 wage: 4.08","educ: 12 wage: 3.75","educ: 8 wage: 3.05","educ: 12 wage: 3.50","educ: 3 wage: 2.92","educ: 11 wage: 4.50","educ: 15 wage: 3.35","educ: 11 wage: 5.95","educ: 12 wage: 8.00","educ: 4 wage: 3.00","educ: 9 wage: 5.00","educ: 12 wage: 5.50","educ: 12 wage: 2.65","educ: 11 wage: 3.00","educ: 12 wage: 4.50","educ: 16 wage: 17.50","educ: 13 wage: 8.18","educ: 15 wage: 9.09","educ: 16 wage: 11.82","educ: 12 wage: 3.25","educ: 12 wage: 4.50","educ: 12 wage: 4.50","educ: 9 wage: 3.71","educ: 10 wage: 6.50","educ: 12 wage: 2.90","educ: 11 wage: 5.60","educ: 8 wage: 2.23","educ: 6 wage: 5.00","educ: 16 wage: 8.33","educ: 12 wage: 2.90","educ: 12 wage: 6.25","educ: 16 wage: 4.55","educ: 12 wage: 3.28","educ: 10 wage: 2.30","educ: 13 wage: 3.30","educ: 13 wage: 3.15","educ: 14 wage: 12.50","educ: 16 wage: 5.15","educ: 10 wage: 3.13","educ: 12 wage: 7.25","educ: 12 wage: 2.90","educ: 11 wage: 1.75","educ: 0 wage: 2.89","educ: 5 wage: 2.90","educ: 16 wage: 17.71","educ: 16 wage: 6.25","educ: 9 wage: 2.60","educ: 15 wage: 6.63","educ: 12 wage: 3.50","educ: 12 wage: 6.50","educ: 12 wage: 3.00","educ: 13 wage: 4.38","educ: 12 wage: 10.00","educ: 7 wage: 4.95","educ: 17 wage: 9.00","educ: 12 wage: 1.43","educ: 12 wage: 3.08","educ: 14 wage: 9.33","educ: 12 wage: 7.50","educ: 13 wage: 4.75","educ: 12 wage: 5.65","educ: 16 wage: 15.00","educ: 10 wage: 2.27","educ: 15 wage: 4.67","educ: 16 wage: 11.56","educ: 14 wage: 3.50"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(145,184,189,1)","opacity":1,"size":5.66929133858268,"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(145,184,189,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":33.8729763387298},"plot_bgcolor":"transparent","paper_bgcolor":"rgba(213,228,235,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.9,18.9],"tickmode":"array","ticktext":["0","5","10","15"],"tickvals":[0,5,10,15],"categoryorder":"array","categoryarray":["0","5","10","15"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":" Years of Education <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.692500007152558,26.2024995207787],"tickmode":"array","ticktext":["0","5","10","15","20","25"],"tickvals":[0,5,10,15,20,25],"categoryorder":"array","categoryarray":["0","5","10","15","20","25"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":" Hourly Wages <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"transparent","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":560,"height":430,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"7944250c7f8d":{"x":{},"y":{},"type":"scatter"}},"cur_data":"7944250c7f8d","visdat":{"7944250c7f8d":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script>

]

---

---

# Conditional Expectation Functions (CEF)

* Frequently, we are interested in conditional expectations: for example, the expected salary for people who have completed three years of schooling. This can be written as `$E[Y_{i}|X_{i}=x]$`, where `$Y_{i}$` is salary, and `$X_{i}=x$` can be read as "when `$X_{i}$` equals the particular value `$x$`" - in our case, when education equals 3 years

* Conditional expectations tell us how one variable's population average changes as we move the conditioning variable over its values. For every value of the conditioning variable, we might get a different average of the dependent variable `$Y_{i}$`, and the collection of all those averages is called the *conditional expectation function*

* The figure shows the conditional expectation of hourly wages given years of education. Despite its ups and downs, the earnings-schooling CEF is upward-sloping

]

.pull-right[
<div id="htmlwidget-8682e72a421bb6f87f1f" style="width:560px;height:430px;" class="plotly html-widget"></div>
<script type="application/json" data-for="htmlwidget-8682e72a421bb6f87f1f">{"x":{"data":[{"x":[0,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18],"y":[3.53000009059906,3.75,2.92000007629395,3.16999999682109,2.90000009536743,3.98499997456869,4.38749992847443,5.03818186846646,3.27588237033171,3.83566667636236,4.18551725354688,5.37136365187289,5.59897439907759,6.23169812166466,6.3214285941351,8.04161766346763,11.3433333237966,10.678947285602],"text":["educ: 0 wage: 3.530000","educ: 2 wage: 3.750000","educ: 3 wage: 2.920000","educ: 4 wage: 3.170000","educ: 5 wage: 2.900000","educ: 6 wage: 3.985000","educ: 7 wage: 4.387500","educ: 8 wage: 5.038182","educ: 9 wage: 3.275882","educ: 10 wage: 3.835667","educ: 11 wage: 4.185517","educ: 12 wage: 5.371364","educ: 13 wage: 5.598974","educ: 14 wage: 6.231698","educ: 15 wage: 6.321429","educ: 16 wage: 8.041618","educ: 17 wage: 11.343333","educ: 18 wage: 10.678947"],"type":"scatter","mode":"markers+lines","marker":{"autocolorscale":false,"color":"rgba(0,0,0,1)","opacity":1,"size":5.66929133858268,"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,0,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","line":{"width":1.88976377952756,"color":"rgba(145,184,189,1)","dash":"solid"},"frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":49.813200498132},"plot_bgcolor":"transparent","paper_bgcolor":"rgba(213,228,235,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.9,18.9],"tickmode":"array","ticktext":["0","5","10","15"],"tickvals":[0,5,10,15],"categoryorder":"array","categoryarray":["0","5","10","15"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":" Years of Education <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[2.47783343394597,11.765499985218],"tickmode":"array","ticktext":["2.5","5.0","7.5","10.0"],"tickvals":[2.5,5,7.5,10],"categoryorder":"array","categoryarray":["2.5","5.0","7.5","10.0"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":" Hourly Wages <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"transparent","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":560,"height":430,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"79444d3e30aa":{"x":{},"y":{},"type":"scatter"},"794474b5bcc":{"x":{},"y":{}}},"cur_data":"79444d3e30aa","visdat":{"79444d3e30aa":["function (y) ","x"],"794474b5bcc":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script>

]
---

# Line Fitting I

* Assuming that the relationship between earnings and education is linear, one can easily apply the most well-known application of line-fitting: the Ordinary Least Squares (OLS)

* OLS picks the line that gives the lowest *sum of squared residuals*. A residual is a difference between an observation's actual value and the conditional mean assigned by the line `$Y-\hat{Y}$`

* Our model of earnings and education can be written as

`$$\underbrace{Y_{i}}_{Wage_{i}}=\beta_{0}+\beta_{1}\underbrace{X_{i}}_{Educ_{i}}+\varepsilon_{i}$$` 
where `$\beta$`'s are unknown parameters to be estimated and `$\varepsilon$` is the unobserved error term

]

<div id="htmlwidget-8eba22ecb268786655eb" style="width:560px;height:430px;" class="plotly html-widget"></div>
<script type="application/json" data-for="htmlwidget-8eba22ecb268786655eb">{"x":{"data":[{"x":[11,12,11,8,12,16,18,12,12,17,16,13,12,12,12,16,12,13,12,12,12,12,16,12,11,16,16,16,15,8,14,14,13,12,12,16,12,4,14,12,12,12,14,11,13,15,10,12,14,12,12,16,12,12,12,15,16,8,18,16,13,14,10,10,14,14,16,12,16,12,16,17,12,12,12,13,12,12,12,18,9,16,10,12,12,12,12,12,8,12,12,14,12,12,12,9,13,12,14,12,15,12,12,12,14,15,12,12,12,17,11,18,12,14,14,10,14,12,15,8,16,14,15,12,18,16,10,8,10,11,18,15,12,11,12,12,14,16,2,14,16,12,12,13,12,15,10,12,16,13,9,12,13,12,12,14,16,16,9,18,10,10,13,12,18,13,12,13,13,13,18,12,12,13,12,12,12,14,10,12,16,16,12,14,12,12,12,12,12,12,12,16,16,14,11,16,12,12,17,12,12,16,8,12,12,12,16,12,12,9,13,16,14,8,14,13,12,18,9,8,8,12,14,12,16,8,13,9,16,12,15,11,14,12,12,12,18,12,12,12,12,12,12,14,16,12,14,11,12,10,12,6,13,12,10,12,14,13,12,18,12,12,12,12,12,8,13,13,14,12,10,16,12,16,12,14,18,17,13,14,15,14,12,8,12,12,8,12,9,12,16,12,16,12,12,13,10,6,12,12,16,12,8,12,6,4,11,11,7,12,18,12,16,12,14,12,10,10,9,10,12,12,12,10,16,16,16,12,12,7,8,16,16,18,13,10,16,14,16,12,9,11,11,12,11,12,12,12,12,14,14,18,12,12,12,11,12,17,16,13,13,12,14,14,11,10,8,14,12,10,17,9,12,12,14,16,12,10,0,14,15,16,12,11,11,12,13,12,13,16,15,16,15,12,18,6,6,12,12,16,9,12,11,10,12,8,9,17,16,11,10,8,13,14,13,11,7,16,12,13,14,16,14,11,8,14,17,10,12,12,18,14,18,12,16,14,12,9,12,12,17,12,15,17,16,12,15,16,12,15,12,12,12,12,16,11,14,14,13,14,12,12,8,12,3,11,15,11,12,4,9,12,12,11,12,16,13,15,16,12,12,12,9,10,12,11,8,6,16,12,12,16,12,10,13,13,14,16,10,12,12,11,0,5,16,16,9,15,12,12,12,13,12,7,17,12,12,14,12,13,12,16,10,15,16,14],"y":[3.09999990463257,3.24000000953674,3,6,5.30000019073486,8.75,11.25,5,3.59999990463257,18.1800003051758,6.25,8.13000011444092,8.77000045776367,5.5,22.2000007629395,17.3299999237061,7.5,10.6300001144409,3.59999990463257,4.5,6.88000011444092,8.47999954223633,6.32999992370605,0.529999971389771,6,9.5600004196167,7.78000020980835,12.5,12.5,3.25,13,4.5,9.68000030517578,5,4.67999982833862,4.26999998092651,6.15000009536743,3.50999999046326,3,6.25,7.80999994277954,10,4.5,4,6.38000011444092,13.6999998092651,1.66999995708466,2.9300000667572,3.65000009536743,2.90000009536743,1.62999999523163,8.60000038146973,5,6,2.5,3.25,3.40000009536743,10,21.6299991607666,4.38000011444092,11.710000038147,12.3900003433228,6.25,3.71000003814697,7.78000020980835,19.9799995422363,6.25,10,5.71000003814697,2,5.71000003814697,13.0799999237061,4.90999984741211,2.91000008583069,3.75,11.8999996185303,4,3.09999990463257,8.44999980926514,7.1399998664856,4.5,4.65000009536743,2.90000009536743,6.67000007629395,3.5,3.25999999046326,3.25,8,9.85000038146973,7.5,5.90999984741211,11.7600002288818,3,4.80999994277954,6.5,4,3.5,13.1599998474121,4.25,3.5,5.13000011444092,3.75,4.5,7.63000011444092,15,6.84999990463257,13.3299999237061,6.67000007629395,2.52999997138977,9.80000019073486,3.36999988555908,24.9799995422363,5.40000009536743,6.1100001335144,4.19999980926514,3.75,3.5,3.64000010490417,3.79999995231628,3,5,4.63000011444092,3,3.20000004768372,3.91000008583069,6.42999982833862,5.48000001907349,1.5,2.90000009536743,5,8.92000007629395,5,3.51999998092651,2.90000009536743,4.5,2.25,5,10,3.75,10,10.9499998092651,7.90000009536743,4.71999979019165,5.84000015258789,3.82999992370605,3.20000004768372,2,4.5,11.5500001907349,2.14000010490417,2.38000011444092,3.75,5.51999998092651,6.5,3.09999990463257,10,6.63000011444092,10,2.30999994277954,6.88000011444092,2.82999992370605,3.13000011444092,8,4.5,8.64999961853027,2,4.75,6.25,6,15.3800001144409,14.5799999237061,12.5,5.25,2.17000007629395,7.1399998664856,6.21999979019165,9,10,5.76999998092651,4,8.75,6.53000020980835,7.59999990463257,5,5,21.8600006103516,8.64000034332275,3.29999995231628,4.44000005722046,4.55000019073486,3.5,6.25,3.84999990463257,6.17999982833862,2.91000008583069,6.25,6.25,9.05000019073486,10,11.1099996566772,6.88000011444092,8.75,10,3.04999995231628,3,5.80000019073486,4.09999990463257,8,6.15000009536743,2.70000004768372,2.75,3,3,7.3600001335144,7.5,3.5,8.10000038146973,3.75,3.25,5.82999992370605,3.5,3.32999992370605,4,3.5,6.25,2.95000004768372,5.71000003814697,3,22.8600006103516,9,8.32999992370605,3,5.75,6.76000022888184,10,3,3.5,3.25,4,2.92000007629395,3.05999994277954,3.20000004768372,4.75,3,18.1599998474121,3.5,4.1100001335144,1.96000003814697,4.28999996185303,3,6.44999980926514,5.19999980926514,4.5,3.88000011444092,3.45000004768372,10.9099998474121,4.09999990463257,3,5.90000009536743,18,4,3,3.54999995231628,3,8.75,2.90000009536743,6.26000022888184,3.5,4.59999990463257,6,2.89000010490417,5.57999992370605,4,6,4.5,2.92000007629395,4.32999992370605,18.8899993896484,4.28000020980835,4.57000017166138,6.25,2.95000004768372,8.75,8.5,3.75,3.15000009536743,5,6.46000003814697,2,4.78999996185303,5.78000020980835,3.1800000667572,4.67999982833862,4.09999990463257,2.91000008583069,6,3.59999990463257,3.95000004768372,7,3,6.07999992370605,8.63000011444092,3,3.75,2.90000009536743,3,6.25,3.5,3,3.24000000953674,8.02000045776367,3.32999992370605,5.25,6.25,3.5,2.95000004768372,3,4.69000005722046,3.73000001907349,4,4,2.90000009536743,3.04999995231628,5.05000019073486,13.9499998092651,18.1599998474121,6.25,5.25,4.78999996185303,3.34999990463257,3,8.43000030517578,5.69999980926514,11.9799995422363,3.5,4.23999977111816,7,6,12.2200002670288,4.5,3,2.90000009536743,15,4,5.25,4,3.29999995231628,5.05000019073486,3.57999992370605,5,4.57000017166138,12.5,3.45000004768372,4.63000011444092,10,2.92000007629395,4.51000022888184,6.5,7.5,3.53999996185303,4.19999980926514,3.50999999046326,4.5,3.34999990463257,2.91000008583069,5.25,4.05000019073486,3.75,3.40000009536743,3,6.28999996185303,2.53999996185303,4.5,3.13000011444092,6.3600001335144,4.67999982833862,6.80000019073486,8.52999973297119,4.17000007629395,3.75,11.1000003814697,3.25999999046326,9.13000011444092,4.5,3,8.75,4.1399998664856,2.86999988555908,3.34999990463257,6.07999992370605,3,4.19999980926514,5.59999990463257,10,12.5,3.75999999046326,3.09999990463257,4.28999996185303,10.9200000762939,7.5,4.05000019073486,4.65000009536743,5,2.90000009536743,8,8.43000030517578,2.92000007629395,6.25,6.25,5.1100001335144,4,4.44000005722046,6.88000011444092,5.42999982833862,3,2.90000009536743,6.25,4.34000015258789,3.25,7.26000022888184,6.34999990463257,5.63000011444092,8.75,3.20000004768372,3,3,12.5,2.88000011444092,3.34999990463257,6.5,10.3800001144409,4.5,10,3.80999994277954,8.80000019073486,9.42000007629395,6.32999992370605,4,2.90000009536743,20,11.25,3.5,6,14.3800001144409,6.3600001335144,3.54999995231628,3,4.5,6.63000011444092,9.30000019073486,3,3.25,1.5,5.90000009536743,8,2.90000009536743,3.28999996185303,6.5,4,6,4.07999992370605,3.75,3.04999995231628,3.5,2.92000007629395,4.5,3.34999990463257,5.94999980926514,8,3,5,5.5,2.65000009536743,3,4.5,17.5,8.18000030517578,9.09000015258789,11.8199996948242,3.25,4.5,4.5,3.71000003814697,6.5,2.90000009536743,5.59999990463257,2.23000001907349,5,8.32999992370605,2.90000009536743,6.25,4.55000019073486,3.27999997138977,2.29999995231628,3.29999995231628,3.15000009536743,12.5,5.15000009536743,3.13000011444092,7.25,2.90000009536743,1.75,2.89000010490417,2.90000009536743,17.7099990844727,6.25,2.59999990463257,6.63000011444092,3.5,6.5,3,4.38000011444092,10,4.94999980926514,9,1.42999994754791,3.07999992370605,9.32999992370605,7.5,4.75,5.65000009536743,15,2.26999998092651,4.67000007629395,11.5600004196167,3.5],"text":["educ: 11 wage: 3.10","educ: 12 wage: 3.24","educ: 11 wage: 3.00","educ: 8 wage: 6.00","educ: 12 wage: 5.30","educ: 16 wage: 8.75","educ: 18 wage: 11.25","educ: 12 wage: 5.00","educ: 12 wage: 3.60","educ: 17 wage: 18.18","educ: 16 wage: 6.25","educ: 13 wage: 8.13","educ: 12 wage: 8.77","educ: 12 wage: 5.50","educ: 12 wage: 22.20","educ: 16 wage: 17.33","educ: 12 wage: 7.50","educ: 13 wage: 10.63","educ: 12 wage: 3.60","educ: 12 wage: 4.50","educ: 12 wage: 6.88","educ: 12 wage: 8.48","educ: 16 wage: 6.33","educ: 12 wage: 0.53","educ: 11 wage: 6.00","educ: 16 wage: 9.56","educ: 16 wage: 7.78","educ: 16 wage: 12.50","educ: 15 wage: 12.50","educ: 8 wage: 3.25","educ: 14 wage: 13.00","educ: 14 wage: 4.50","educ: 13 wage: 9.68","educ: 12 wage: 5.00","educ: 12 wage: 4.68","educ: 16 wage: 4.27","educ: 12 wage: 6.15","educ: 4 wage: 3.51","educ: 14 wage: 3.00","educ: 12 wage: 6.25","educ: 12 wage: 7.81","educ: 12 wage: 10.00","educ: 14 wage: 4.50","educ: 11 wage: 4.00","educ: 13 wage: 6.38","educ: 15 wage: 13.70","educ: 10 wage: 1.67","educ: 12 wage: 2.93","educ: 14 wage: 3.65","educ: 12 wage: 2.90","educ: 12 wage: 1.63","educ: 16 wage: 8.60","educ: 12 wage: 5.00","educ: 12 wage: 6.00","educ: 12 wage: 2.50","educ: 15 wage: 3.25","educ: 16 wage: 3.40","educ: 8 wage: 10.00","educ: 18 wage: 21.63","educ: 16 wage: 4.38","educ: 13 wage: 11.71","educ: 14 wage: 12.39","educ: 10 wage: 6.25","educ: 10 wage: 3.71","educ: 14 wage: 7.78","educ: 14 wage: 19.98","educ: 16 wage: 6.25","educ: 12 wage: 10.00","educ: 16 wage: 5.71","educ: 12 wage: 2.00","educ: 16 wage: 5.71","educ: 17 wage: 13.08","educ: 12 wage: 4.91","educ: 12 wage: 2.91","educ: 12 wage: 3.75","educ: 13 wage: 11.90","educ: 12 wage: 4.00","educ: 12 wage: 3.10","educ: 12 wage: 8.45","educ: 18 wage: 7.14","educ: 9 wage: 4.50","educ: 16 wage: 4.65","educ: 10 wage: 2.90","educ: 12 wage: 6.67","educ: 12 wage: 3.50","educ: 12 wage: 3.26","educ: 12 wage: 3.25","educ: 12 wage: 8.00","educ: 8 wage: 9.85","educ: 12 wage: 7.50","educ: 12 wage: 5.91","educ: 14 wage: 11.76","educ: 12 wage: 3.00","educ: 12 wage: 4.81","educ: 12 wage: 6.50","educ: 9 wage: 4.00","educ: 13 wage: 3.50","educ: 12 wage: 13.16","educ: 14 wage: 4.25","educ: 12 wage: 3.50","educ: 15 wage: 5.13","educ: 12 wage: 3.75","educ: 12 wage: 4.50","educ: 12 wage: 7.63","educ: 14 wage: 15.00","educ: 15 wage: 6.85","educ: 12 wage: 13.33","educ: 12 wage: 6.67","educ: 12 wage: 2.53","educ: 17 wage: 9.80","educ: 11 wage: 3.37","educ: 18 wage: 24.98","educ: 12 wage: 5.40","educ: 14 wage: 6.11","educ: 14 wage: 4.20","educ: 10 wage: 3.75","educ: 14 wage: 3.50","educ: 12 wage: 3.64","educ: 15 wage: 3.80","educ: 8 wage: 3.00","educ: 16 wage: 5.00","educ: 14 wage: 4.63","educ: 15 wage: 3.00","educ: 12 wage: 3.20","educ: 18 wage: 3.91","educ: 16 wage: 6.43","educ: 10 wage: 5.48","educ: 8 wage: 1.50","educ: 10 wage: 2.90","educ: 11 wage: 5.00","educ: 18 wage: 8.92","educ: 15 wage: 5.00","educ: 12 wage: 3.52","educ: 11 wage: 2.90","educ: 12 wage: 4.50","educ: 12 wage: 2.25","educ: 14 wage: 5.00","educ: 16 wage: 10.00","educ: 2 wage: 3.75","educ: 14 wage: 10.00","educ: 16 wage: 10.95","educ: 12 wage: 7.90","educ: 12 wage: 4.72","educ: 13 wage: 5.84","educ: 12 wage: 3.83","educ: 15 wage: 3.20","educ: 10 wage: 2.00","educ: 12 wage: 4.50","educ: 16 wage: 11.55","educ: 13 wage: 2.14","educ: 9 wage: 2.38","educ: 12 wage: 3.75","educ: 13 wage: 5.52","educ: 12 wage: 6.50","educ: 12 wage: 3.10","educ: 14 wage: 10.00","educ: 16 wage: 6.63","educ: 16 wage: 10.00","educ: 9 wage: 2.31","educ: 18 wage: 6.88","educ: 10 wage: 2.83","educ: 10 wage: 3.13","educ: 13 wage: 8.00","educ: 12 wage: 4.50","educ: 18 wage: 8.65","educ: 13 wage: 2.00","educ: 12 wage: 4.75","educ: 13 wage: 6.25","educ: 13 wage: 6.00","educ: 13 wage: 15.38","educ: 18 wage: 14.58","educ: 12 wage: 12.50","educ: 12 wage: 5.25","educ: 13 wage: 2.17","educ: 12 wage: 7.14","educ: 12 wage: 6.22","educ: 12 wage: 9.00","educ: 14 wage: 10.00","educ: 10 wage: 5.77","educ: 12 wage: 4.00","educ: 16 wage: 8.75","educ: 16 wage: 6.53","educ: 12 wage: 7.60","educ: 14 wage: 5.00","educ: 12 wage: 5.00","educ: 12 wage: 21.86","educ: 12 wage: 8.64","educ: 12 wage: 3.30","educ: 12 wage: 4.44","educ: 12 wage: 4.55","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 16 wage: 3.85","educ: 14 wage: 6.18","educ: 11 wage: 2.91","educ: 16 wage: 6.25","educ: 12 wage: 6.25","educ: 12 wage: 9.05","educ: 17 wage: 10.00","educ: 12 wage: 11.11","educ: 12 wage: 6.88","educ: 16 wage: 8.75","educ: 8 wage: 10.00","educ: 12 wage: 3.05","educ: 12 wage: 3.00","educ: 12 wage: 5.80","educ: 16 wage: 4.10","educ: 12 wage: 8.00","educ: 12 wage: 6.15","educ: 9 wage: 2.70","educ: 13 wage: 2.75","educ: 16 wage: 3.00","educ: 14 wage: 3.00","educ: 8 wage: 7.36","educ: 14 wage: 7.50","educ: 13 wage: 3.50","educ: 12 wage: 8.10","educ: 18 wage: 3.75","educ: 9 wage: 3.25","educ: 8 wage: 5.83","educ: 8 wage: 3.50","educ: 12 wage: 3.33","educ: 14 wage: 4.00","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 8 wage: 2.95","educ: 13 wage: 5.71","educ: 9 wage: 3.00","educ: 16 wage: 22.86","educ: 12 wage: 9.00","educ: 15 wage: 8.33","educ: 11 wage: 3.00","educ: 14 wage: 5.75","educ: 12 wage: 6.76","educ: 12 wage: 10.00","educ: 12 wage: 3.00","educ: 18 wage: 3.50","educ: 12 wage: 3.25","educ: 12 wage: 4.00","educ: 12 wage: 2.92","educ: 12 wage: 3.06","educ: 12 wage: 3.20","educ: 12 wage: 4.75","educ: 14 wage: 3.00","educ: 16 wage: 18.16","educ: 12 wage: 3.50","educ: 14 wage: 4.11","educ: 11 wage: 1.96","educ: 12 wage: 4.29","educ: 10 wage: 3.00","educ: 12 wage: 6.45","educ: 6 wage: 5.20","educ: 13 wage: 4.50","educ: 12 wage: 3.88","educ: 10 wage: 3.45","educ: 12 wage: 10.91","educ: 14 wage: 4.10","educ: 13 wage: 3.00","educ: 12 wage: 5.90","educ: 18 wage: 18.00","educ: 12 wage: 4.00","educ: 12 wage: 3.00","educ: 12 wage: 3.55","educ: 12 wage: 3.00","educ: 12 wage: 8.75","educ: 8 wage: 2.90","educ: 13 wage: 6.26","educ: 13 wage: 3.50","educ: 14 wage: 4.60","educ: 12 wage: 6.00","educ: 10 wage: 2.89","educ: 16 wage: 5.58","educ: 12 wage: 4.00","educ: 16 wage: 6.00","educ: 12 wage: 4.50","educ: 14 wage: 2.92","educ: 18 wage: 4.33","educ: 17 wage: 18.89","educ: 13 wage: 4.28","educ: 14 wage: 4.57","educ: 15 wage: 6.25","educ: 14 wage: 2.95","educ: 12 wage: 8.75","educ: 8 wage: 8.50","educ: 12 wage: 3.75","educ: 12 wage: 3.15","educ: 8 wage: 5.00","educ: 12 wage: 6.46","educ: 9 wage: 2.00","educ: 12 wage: 4.79","educ: 16 wage: 5.78","educ: 12 wage: 3.18","educ: 16 wage: 4.68","educ: 12 wage: 4.10","educ: 12 wage: 2.91","educ: 13 wage: 6.00","educ: 10 wage: 3.60","educ: 6 wage: 3.95","educ: 12 wage: 7.00","educ: 12 wage: 3.00","educ: 16 wage: 6.08","educ: 12 wage: 8.63","educ: 8 wage: 3.00","educ: 12 wage: 3.75","educ: 6 wage: 2.90","educ: 4 wage: 3.00","educ: 11 wage: 6.25","educ: 11 wage: 3.50","educ: 7 wage: 3.00","educ: 12 wage: 3.24","educ: 18 wage: 8.02","educ: 12 wage: 3.33","educ: 16 wage: 5.25","educ: 12 wage: 6.25","educ: 14 wage: 3.50","educ: 12 wage: 2.95","educ: 10 wage: 3.00","educ: 10 wage: 4.69","educ: 9 wage: 3.73","educ: 10 wage: 4.00","educ: 12 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 3.05","educ: 10 wage: 5.05","educ: 16 wage: 13.95","educ: 16 wage: 18.16","educ: 16 wage: 6.25","educ: 12 wage: 5.25","educ: 12 wage: 4.79","educ: 7 wage: 3.35","educ: 8 wage: 3.00","educ: 16 wage: 8.43","educ: 16 wage: 5.70","educ: 18 wage: 11.98","educ: 13 wage: 3.50","educ: 10 wage: 4.24","educ: 16 wage: 7.00","educ: 14 wage: 6.00","educ: 16 wage: 12.22","educ: 12 wage: 4.50","educ: 9 wage: 3.00","educ: 11 wage: 2.90","educ: 11 wage: 15.00","educ: 12 wage: 4.00","educ: 11 wage: 5.25","educ: 12 wage: 4.00","educ: 12 wage: 3.30","educ: 12 wage: 5.05","educ: 12 wage: 3.58","educ: 14 wage: 5.00","educ: 14 wage: 4.57","educ: 18 wage: 12.50","educ: 12 wage: 3.45","educ: 12 wage: 4.63","educ: 12 wage: 10.00","educ: 11 wage: 2.92","educ: 12 wage: 4.51","educ: 17 wage: 6.50","educ: 16 wage: 7.50","educ: 13 wage: 3.54","educ: 13 wage: 4.20","educ: 12 wage: 3.51","educ: 14 wage: 4.50","educ: 14 wage: 3.35","educ: 11 wage: 2.91","educ: 10 wage: 5.25","educ: 8 wage: 4.05","educ: 14 wage: 3.75","educ: 12 wage: 3.40","educ: 10 wage: 3.00","educ: 17 wage: 6.29","educ: 9 wage: 2.54","educ: 12 wage: 4.50","educ: 12 wage: 3.13","educ: 14 wage: 6.36","educ: 16 wage: 4.68","educ: 12 wage: 6.80","educ: 10 wage: 8.53","educ: 0 wage: 4.17","educ: 14 wage: 3.75","educ: 15 wage: 11.10","educ: 16 wage: 3.26","educ: 12 wage: 9.13","educ: 11 wage: 4.50","educ: 11 wage: 3.00","educ: 12 wage: 8.75","educ: 13 wage: 4.14","educ: 12 wage: 2.87","educ: 13 wage: 3.35","educ: 16 wage: 6.08","educ: 15 wage: 3.00","educ: 16 wage: 4.20","educ: 15 wage: 5.60","educ: 12 wage: 10.00","educ: 18 wage: 12.50","educ: 6 wage: 3.76","educ: 6 wage: 3.10","educ: 12 wage: 4.29","educ: 12 wage: 10.92","educ: 16 wage: 7.50","educ: 9 wage: 4.05","educ: 12 wage: 4.65","educ: 11 wage: 5.00","educ: 10 wage: 2.90","educ: 12 wage: 8.00","educ: 8 wage: 8.43","educ: 9 wage: 2.92","educ: 17 wage: 6.25","educ: 16 wage: 6.25","educ: 11 wage: 5.11","educ: 10 wage: 4.00","educ: 8 wage: 4.44","educ: 13 wage: 6.88","educ: 14 wage: 5.43","educ: 13 wage: 3.00","educ: 11 wage: 2.90","educ: 7 wage: 6.25","educ: 16 wage: 4.34","educ: 12 wage: 3.25","educ: 13 wage: 7.26","educ: 14 wage: 6.35","educ: 16 wage: 5.63","educ: 14 wage: 8.75","educ: 11 wage: 3.20","educ: 8 wage: 3.00","educ: 14 wage: 3.00","educ: 17 wage: 12.50","educ: 10 wage: 2.88","educ: 12 wage: 3.35","educ: 12 wage: 6.50","educ: 18 wage: 10.38","educ: 14 wage: 4.50","educ: 18 wage: 10.00","educ: 12 wage: 3.81","educ: 16 wage: 8.80","educ: 14 wage: 9.42","educ: 12 wage: 6.33","educ: 9 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 20.00","educ: 17 wage: 11.25","educ: 12 wage: 3.50","educ: 15 wage: 6.00","educ: 17 wage: 14.38","educ: 16 wage: 6.36","educ: 12 wage: 3.55","educ: 15 wage: 3.00","educ: 16 wage: 4.50","educ: 12 wage: 6.63","educ: 15 wage: 9.30","educ: 12 wage: 3.00","educ: 12 wage: 3.25","educ: 12 wage: 1.50","educ: 12 wage: 5.90","educ: 16 wage: 8.00","educ: 11 wage: 2.90","educ: 14 wage: 3.29","educ: 14 wage: 6.50","educ: 13 wage: 4.00","educ: 14 wage: 6.00","educ: 12 wage: 4.08","educ: 12 wage: 3.75","educ: 8 wage: 3.05","educ: 12 wage: 3.50","educ: 3 wage: 2.92","educ: 11 wage: 4.50","educ: 15 wage: 3.35","educ: 11 wage: 5.95","educ: 12 wage: 8.00","educ: 4 wage: 3.00","educ: 9 wage: 5.00","educ: 12 wage: 5.50","educ: 12 wage: 2.65","educ: 11 wage: 3.00","educ: 12 wage: 4.50","educ: 16 wage: 17.50","educ: 13 wage: 8.18","educ: 15 wage: 9.09","educ: 16 wage: 11.82","educ: 12 wage: 3.25","educ: 12 wage: 4.50","educ: 12 wage: 4.50","educ: 9 wage: 3.71","educ: 10 wage: 6.50","educ: 12 wage: 2.90","educ: 11 wage: 5.60","educ: 8 wage: 2.23","educ: 6 wage: 5.00","educ: 16 wage: 8.33","educ: 12 wage: 2.90","educ: 12 wage: 6.25","educ: 16 wage: 4.55","educ: 12 wage: 3.28","educ: 10 wage: 2.30","educ: 13 wage: 3.30","educ: 13 wage: 3.15","educ: 14 wage: 12.50","educ: 16 wage: 5.15","educ: 10 wage: 3.13","educ: 12 wage: 7.25","educ: 12 wage: 2.90","educ: 11 wage: 1.75","educ: 0 wage: 2.89","educ: 5 wage: 2.90","educ: 16 wage: 17.71","educ: 16 wage: 6.25","educ: 9 wage: 2.60","educ: 15 wage: 6.63","educ: 12 wage: 3.50","educ: 12 wage: 6.50","educ: 12 wage: 3.00","educ: 13 wage: 4.38","educ: 12 wage: 10.00","educ: 7 wage: 4.95","educ: 17 wage: 9.00","educ: 12 wage: 1.43","educ: 12 wage: 3.08","educ: 14 wage: 9.33","educ: 12 wage: 7.50","educ: 13 wage: 4.75","educ: 12 wage: 5.65","educ: 16 wage: 15.00","educ: 10 wage: 2.27","educ: 15 wage: 4.67","educ: 16 wage: 11.56","educ: 14 wage: 3.50"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(145,184,189,1)","opacity":1,"size":5.66929133858268,"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(145,184,189,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[0,0.227848101265823,0.455696202531646,0.683544303797468,0.911392405063291,1.13924050632911,1.36708860759494,1.59493670886076,1.82278481012658,2.0506329113924,2.27848101265823,2.50632911392405,2.73417721518987,2.9620253164557,3.18987341772152,3.41772151898734,3.64556962025316,3.87341772151899,4.10126582278481,4.32911392405063,4.55696202531646,4.78481012658228,5.0126582278481,5.24050632911392,5.46835443037975,5.69620253164557,5.92405063291139,6.15189873417722,6.37974683544304,6.60759493670886,6.83544303797468,7.06329113924051,7.29113924050633,7.51898734177215,7.74683544303797,7.9746835443038,8.20253164556962,8.43037974683544,8.65822784810127,8.88607594936709,9.11392405063291,9.34177215189873,9.56962025316456,9.79746835443038,10.0253164556962,10.253164556962,10.4810126582278,10.7088607594937,10.9367088607595,11.1645569620253,11.3924050632911,11.620253164557,11.8481012658228,12.0759493670886,12.3037974683544,12.5316455696203,12.7594936708861,12.9873417721519,13.2151898734177,13.4430379746835,13.6708860759494,13.8987341772152,14.126582278481,14.3544303797468,14.5822784810127,14.8101265822785,15.0379746835443,15.2658227848101,15.4936708860759,15.7215189873418,15.9493670886076,16.1772151898734,16.4050632911392,16.6329113924051,16.8607594936709,17.0886075949367,17.3164556962025,17.5443037974684,17.7721518987342,18],"y":[-0.904851611957259,-0.781503933679118,-0.658156255400976,-0.534808577122835,-0.411460898844693,-0.288113220566552,-0.16476554228841,-0.0414178640102687,0.0819298142678727,0.205277492546014,0.328625170824156,0.451972849102297,0.575320527380439,0.69866820565858,0.822015883936722,0.945363562214863,1.068711240493,1.19205891877115,1.31540659704929,1.43875427532743,1.56210195360557,1.68544963188371,1.80879731016185,1.93214498844,2.05549266671814,2.17884034499628,2.30218802327442,2.42553570155256,2.5488833798307,2.67223105810884,2.79557873638699,2.91892641466513,3.04227409294327,3.16562177122141,3.28896944949955,3.41231712777769,3.53566480605583,3.65901248433398,3.78236016261212,3.90570784089026,4.0290555191684,4.15240319744654,4.27575087572468,4.39909855400282,4.52244623228097,4.64579391055911,4.76914158883725,4.89248926711539,5.01583694539353,5.13918462367167,5.26253230194982,5.38587998022796,5.5092276585061,5.63257533678424,5.75592301506238,5.87927069334052,6.00261837161866,6.12596604989681,6.24931372817495,6.37266140645309,6.49600908473123,6.61935676300937,6.74270444128751,6.86605211956565,6.9893997978438,7.11274747612194,7.23609515440008,7.35944283267822,7.48279051095636,7.6061381892345,7.72948586751265,7.85283354579079,7.97618122406893,8.09952890234707,8.22287658062521,8.34622425890335,8.46957193718149,8.59291961545964,8.71626729373778,8.83961497201592],"text":["educ: 0.0000000 wage: -0.90485161","educ: 0.2278481 wage: -0.78150393","educ: 0.4556962 wage: -0.65815626","educ: 0.6835443 wage: -0.53480858","educ: 0.9113924 wage: -0.41146090","educ: 1.1392405 wage: -0.28811322","educ: 1.3670886 wage: -0.16476554","educ: 1.5949367 wage: -0.04141786","educ: 1.8227848 wage: 0.08192981","educ: 2.0506329 wage: 0.20527749","educ: 2.2784810 wage: 0.32862517","educ: 2.5063291 wage: 0.45197285","educ: 2.7341772 wage: 0.57532053","educ: 2.9620253 wage: 0.69866821","educ: 3.1898734 wage: 0.82201588","educ: 3.4177215 wage: 0.94536356","educ: 3.6455696 wage: 1.06871124","educ: 3.8734177 wage: 1.19205892","educ: 4.1012658 wage: 1.31540660","educ: 4.3291139 wage: 1.43875428","educ: 4.5569620 wage: 1.56210195","educ: 4.7848101 wage: 1.68544963","educ: 5.0126582 wage: 1.80879731","educ: 5.2405063 wage: 1.93214499","educ: 5.4683544 wage: 2.05549267","educ: 5.6962025 wage: 2.17884034","educ: 5.9240506 wage: 2.30218802","educ: 6.1518987 wage: 2.42553570","educ: 6.3797468 wage: 2.54888338","educ: 6.6075949 wage: 2.67223106","educ: 6.8354430 wage: 2.79557874","educ: 7.0632911 wage: 2.91892641","educ: 7.2911392 wage: 3.04227409","educ: 7.5189873 wage: 3.16562177","educ: 7.7468354 wage: 3.28896945","educ: 7.9746835 wage: 3.41231713","educ: 8.2025316 wage: 3.53566481","educ: 8.4303797 wage: 3.65901248","educ: 8.6582278 wage: 3.78236016","educ: 8.8860759 wage: 3.90570784","educ: 9.1139241 wage: 4.02905552","educ: 9.3417722 wage: 4.15240320","educ: 9.5696203 wage: 4.27575088","educ: 9.7974684 wage: 4.39909855","educ: 10.0253165 wage: 4.52244623","educ: 10.2531646 wage: 4.64579391","educ: 10.4810127 wage: 4.76914159","educ: 10.7088608 wage: 4.89248927","educ: 10.9367089 wage: 5.01583695","educ: 11.1645570 wage: 5.13918462","educ: 11.3924051 wage: 5.26253230","educ: 11.6202532 wage: 5.38587998","educ: 11.8481013 wage: 5.50922766","educ: 12.0759494 wage: 5.63257534","educ: 12.3037975 wage: 5.75592302","educ: 12.5316456 wage: 5.87927069","educ: 12.7594937 wage: 6.00261837","educ: 12.9873418 wage: 6.12596605","educ: 13.2151899 wage: 6.24931373","educ: 13.4430380 wage: 6.37266141","educ: 13.6708861 wage: 6.49600908","educ: 13.8987342 wage: 6.61935676","educ: 14.1265823 wage: 6.74270444","educ: 14.3544304 wage: 6.86605212","educ: 14.5822785 wage: 6.98939980","educ: 14.8101266 wage: 7.11274748","educ: 15.0379747 wage: 7.23609515","educ: 15.2658228 wage: 7.35944283","educ: 15.4936709 wage: 7.48279051","educ: 15.7215190 wage: 7.60613819","educ: 15.9493671 wage: 7.72948587","educ: 16.1772152 wage: 7.85283355","educ: 16.4050633 wage: 7.97618122","educ: 16.6329114 wage: 8.09952890","educ: 16.8607595 wage: 8.22287658","educ: 17.0886076 wage: 8.34622426","educ: 17.3164557 wage: 8.46957194","educ: 17.5443038 wage: 8.59291962","educ: 17.7721519 wage: 8.71626729","educ: 18.0000000 wage: 8.83961497"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(51,102,102,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":33.8729763387298},"plot_bgcolor":"transparent","paper_bgcolor":"rgba(213,228,235,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.9,18.9],"tickmode":"array","ticktext":["0","5","10","15"],"tickvals":[0,5,10,15],"categoryorder":"array","categoryarray":["0","5","10","15"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":" Years of Education <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-2.19909416966694,26.274242099946],"tickmode":"array","ticktext":["0","5","10","15","20","25"],"tickvals":[0,5,10,15,20,25],"categoryorder":"array","categoryarray":["0","5","10","15","20","25"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":" Hourly Wages <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"transparent","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":560,"height":430,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"7944db26fc4":{"x":{},"y":{},"type":"scatter"},"79446cb446e9":{"x":{},"y":{}}},"cur_data":"7944db26fc4","visdat":{"7944db26fc4":["function (y) ","x"],"79446cb446e9":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script>

]

---

# Line Fitting II

Ultimately, the goal is to minimize `$\sum e_{i}^{2}$`, where `$e_{i}=Y_{i}-\underbrace{\hat{Y}_{i}}_{Prediction}$`. In other words, we estimate `$\beta_{0}$` and `$\beta_{1}$` by minimizing the sum of squared deviations from the regression line:

`$$(\hat{\beta}_{0}, \hat{\beta}_{1})=\underset{\beta_{0}, \beta_{1}}{\arg\min} \sum_{i=1}^{n} (Y_{i}-\beta_{0}-\beta_{1}X_{i})^{2}$$`
which leads to:
`$$\hat{\beta_{0}}= \bar{Y} - \hat{\beta_{1}}\bar{X} \\
\hat{\beta_{1}}=\frac{\sum_{i=1}^{n}(X_{i}-\bar{X})(Y_{i}-\bar{Y})}{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}=\frac{Cov(X_{i}, Y_{i})}{Var(X_{i})}$$`

**OLS** gives us the best linear approximation of the relationship between `$X$` and `$Y$`
]

* The table shows the results of the linear regression. As you can see, `$\hat{\beta}_{0}=-0.905$` and `$\hat{\beta}_{1}=0.541$`. Hence, the OLS selected the best-fit values of `$\beta_{0}$` and `$\beta_{1}$` to give us

`$$\widehat{Wage_{i}}=-0.905+0.541Educ_{i}$$`
* So, we would expect a 0.541 increase in the conditional mean of the hourly wage for a one-year increase in education. Also, for someone with three years of schooling, the predicted hourly wage (in 1976) according to our model is `$-0.905+0.541\times 3=0.718$`. You can check the scatterplot and see that the individual with three years of education in the sample has an hourly salary of 2.92.

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.541*** (0.053)</td></tr>
<tr><td style="text-align:left">Constant</td><td>-0.905 (0.685)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.163</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>
]
]

```r
#library(stargazer)
# install.packages("wooldridge") if you don't have the package
# install.packages("stargazer") if you don't have the package
#library(stargazer)
library(wooldridge)
data("wage1", package = "wooldridge") # load data
reg<-lm(wage~educ, data=wage1)
summary(reg)
#stargazer(reg, header = F, single.row = TRUE, no.space = T, dep.var.labels.include = FALSE,dep.var.caption = "Hourly Wages", type='html', omit.stat=c("rsq", "ser", "f"))
```

]

---
# The CEF is All You Need

Fun fact: the solution to this problem

`$$\hat{\beta}=\underset{\beta}{\arg\min} \{ (E[Y_{i}|X_{i}]-X^{'}\beta)^{2} \}$$`
is the same as this

`$$\hat{\beta}=\underset{\beta}{\arg\min} \{ (Y_{i}-X^{'}\beta)^{2} \}$$`
The implication of that is you only need conditional means to run regressions. For example, the table shows the results of a **weighted** (*by what?*) linear regression using means by years of schooling instead of individual-level data. As you can see, `$\hat{\beta}_{0}=-0.905$` and `$\hat{\beta}_{1}=0.541$`, same as before (when using individual-level data).

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.541*** (0.081)</td></tr>
<tr><td style="text-align:left">Constant</td><td>-0.905 (1.043)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>18</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.719</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>

]
]

```r
library(stargazer)
wage2<-wage1%>%group_by(educ)%>%summarize(wage=mean(wage), count=n())
reg2<-lm(wage~educ, weights = count, data=wage2)
summary(reg2)
#stargazer(reg2, header = F, single.row = TRUE, no.space = T, dep.var.labels.include = FALSE,dep.var.caption = "Hourly Wages", type='html', omit.stat=c("rsq", "ser", "f"))
```

]

---

# Fits and Residuals

As you just saw, regression breaks any dependent variable into two pieces:

`$$Y_{i}=\hat{Y_{i}}+e_{i}$$`
`$\hat{Y}_{i}$` is the fitted value or the part of `$Y_{i}$` that the model explains. The residual `$e_{i}$` is what is left over.

Some of the residuals properties:

1. Regression residuals have expectation zero (i.e., `$E(e_{i})=0$`)

2. Regression residuals are uncorrelated with all the regressors that made them and with the corresponding fitted value: `$E(X_{ik}e_{i})=0$` for each regressor `$X_{ik}$`. In other words, if you regress `$e_{i}$` on `$X_{1i}, X_{2i}, \dots$`, the estimated coefficients will be equal to zero.

3. Regression residuals are uncorrelated with the corresponding fitted values: `$E(\hat{Y}_{i}e_{i})=0$`

Those properties can be derived using the first-order conditions we used to get `$\hat{\beta}_{0}$` and `$\hat{\beta}_{1}$`.

---
# Regression for Dummies

An important case using regression is the bivariate regression with a dummy regressor (we saw it [here](https://guerramarcelino.github.io/Econ474/Rlabs/lab1#equivalence-of-differences-in-means-and-regression)). Say `$Z_{i}$` takes on two values: 0 and 1. Hence, one can write it as

`$$E[Y_{i}|Z_{i}=0]=\beta_{0} \\
E[Y_{i}|Z_{i}=1]=\beta_{0}+\beta_{1}$$`

so that `$\beta_{1}=E[Y_{i}|Z_{i}=1]-E[Y_{i}|Z_{i}=0]$`.

Using this notation, we can write

`$$E[Y_{i}|Z_{i}]=E[Y_{i}|Z_{i}=0]+(E[Y_{i}|Z_{i}=1]-E[Y_{i}|Z_{i}=0])Z_{i} = \beta_{0}+\beta_{1}Z_{i}$$`

Does it look familiar? This shows that `$E[Y_{i}|Z_{i}]$` is a linear function of `$Z_{i}$`, with slope `$\beta_{1}$` and intercept `$\beta_{0}$`. Because the CEF with a single dummy variable is linear, regression fits this CEF perfectly.

---
# Controlling for Variables

The most exciting regressions include more than one variable. Let's recap bivariate regression:

`$$\hat{\beta_{0}}= \bar{Y} - \hat{\beta_{1}}\bar{X}\\ \hat{\beta_{1}}=\frac{Cov(X_{i}, Y_{i})}{Var(X_{i})}$$`

**With multiple regressors**, the `$k-th$` slope coefficient is:

`$$\beta_{k}=\frac{Cov(Y_{i}, \tilde{x}_{ki})}{V(\tilde{x}_{ki})}$$`
where `$\tilde{x}_{ki}$` is the residual from a regression of `$x_{ki}$` on all the other covariates. Each coefficient in a multivariate regression is the bivariate slope coefficient for the corresponding regressor, after "partialling out" the other variables in the model.

]

In other words, you can think about residuals as the part of `$Y$` that has nothing to do with `$X$`. Back to the wages *versus* education example, we saw that the predicted value for `$Wage$` given `$Educ=3$` was equal to 0.718, far from the observed value of 2.92. It looks like education can only be responsible for 0.718, and the extra 2.202 must be because of some other part of the data generating process.

Let's expand the analysis and include other variables such as `experience`. We would like to know how much of a relationship between wage and education is not explained by experience. To do that, we can:

1. Run a regression between `$Y$` (wage) and `$Z$` (experience), and get the residuals `$Y^{R}$`
2. Run a regression between `$X$` (education) and `$Z$` (experience), and get the residuals `$X^{R}$`
3. Run a regression between `$Y^{R}$` and `$X^{R}$`

This particular set of calculations is known as **Frisch-Waugh-Lovell theorem**.

**What if you do not observe a variable you should include in this model (e.g., ability)?**

]

* Since `$Y^{R}$` and `$X^{R}$` have had the parts of `$Y$` and `$X$` that can be explained with `$Z$` removed, the relationship between `$Y^{R}$` and `$X^{R}$` is the part of the relationship between `$Y$` and `$X$` that is not explained by `$Z$`

* During this process, we are washing out all the variation related to `$Z$`, in effect not allowing `$Z$` to vary. This is why we call the process "controlling for `$Z$`"/"adjusting for `$Z$`".

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>YR</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">XR</td><td>0.644*** (0.054)</td></tr>
<tr><td style="text-align:left">Constant</td><td>0.000 (0.142)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.214</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>
]

]

If you run the regression model

`$$Wage_{i}=\beta_{0}+\beta_{1}Educ_{i}+\beta_{2}Exper_{i}+\varepsilon_{i}$$`

you'll get the same result for the variable of interest `$Educ$`. The OLS estimate for `$\beta_{1}$` represents the relationship between earnings and schooling *conditional on experience*. **Even better**, we can add more controls such as gender, race, etc.

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.644*** (0.054)</td></tr>
<tr><td style="text-align:left">exper</td><td>0.070*** (0.011)</td></tr>
<tr><td style="text-align:left">Constant</td><td>-3.391*** (0.767)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.222</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>

]

---

# Building Models with Logs I

Frequently, economists transform variables using the natural logarithm. For instance, wages are approximately log-normally distributed, and you might want to use `$ln(Wage)$` as a dependent variable instead of `$Wage$` to model the relationship between earnings vs. schooling - in that way, `$ln(Wage)$` would be approximately normally distributed. Taking the log also reduces the impact of outliers, and the estimates have a convenient interpretation.

To see what happens, let's go back to the bivariate regression with dummies example, modifying the dependent variable:

`$$ln(Y_{i})=\beta_{0}+\beta_{1}Z_{i}+\varepsilon_{i}$$`
where `$Z_{i}$` takes on two values: 0 and 1. We can rewrite the equation as `$$E[ln(Y_{i})|Z_{i}]=\beta_{0}+\beta_{1}Z_{i}$$`
and the regression, in this case, fits the CEF perfectly.

Suppose we engineer a *ceteris paribus* change in `$Z_{i}$` for individual `$i$`. This reveals potential outcome `$Y_{0i}$` when `$Z_{i}=0$` and `$Y_{1i}$` when `$Z_{i}=1$` (cont.)

---
# Building Models with Logs II

Rewriting the equation for log of potential outcomes:

`$$ln(Y_{0i})=\beta_{0}+\varepsilon_{i}\\ ln(Y_{1i})=\beta_{0}+\beta_{1}+\varepsilon_{i}$$`

The difference in potential outcomes is

`$$ln(Y_{1i})-ln(Y_{0i})=\beta_{1}$$`
Further rearranging this term:

`$$\beta_{1}=ln(\frac{Y_{1i}}{Y_{0i}})=ln(1+\frac{Y_{1i}-Y_{0i}}{Y_{0i}})=ln(1+\Delta \%Y_{p})\approx\Delta \%Y_{p}$$`
assuming a small `$\Delta \%Y_{p}$`.

`$\Delta \%Y_{p}$` is shorthand for the **percentage change in potential outcomes induced by `$Z_{i}$`**.

]

Running the earnings vs schooling regression in the *log-linear* form

`$$ln(Wage_{i})=\beta_{0}+\beta_{1}Educ_{i}+\varepsilon_{i}$$`
you get the results that the table displays. The interpretation of `$\beta_{1}$` is the following: **an additional year of education increases the hourly wage, on average, by 8.3%.**

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.083*** (0.008)</td></tr>
<tr><td style="text-align:left">Constant</td><td>0.584*** (0.097)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.184</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>

]

---

# Regression Standard Errors

So far, we did not give too much attention to the fact that our data comes from samples. Just like [sample means](https://guerramarcelino.github.io/Econ474/Rlabs/lab2), sample regression estimates are subject to **sampling variance**. Every time that we draw a new sample from the same population to estimate the same regression model, we might get different results. Again, one needs to have in mind how to quantify the uncertainty that arises with sampling.

In the regression framework, we also measure variability with the standard error. In a bivariate regression `$Y_{i}=\beta_{0}+\beta_{1}X_{i}+\varepsilon_{i}$`, the standard error of the slope can be written as

`$$SE(\hat{\beta}_{1})=\frac{\sigma_{e}}{\sigma_{X}\sqrt{n-2}}$$`
where `$\sigma_{e}$` is the standard deviation of the regression residuals, and `$\sigma_{X}$` is the standard deviation of the regressor `$X_{i}$`. Like the standard error of a sample average, regression SEs decrease with *i)* sample size `$\uparrow n$` *ii)* variability in the explanatory variable `$\uparrow \sigma_{X}$`. When the residual variance is large, regression estimates are not precise - in this case, the line does not fit the dots very well.

]

In a multivariate model

`$$Y_{i}=\beta_{0}+\sum_{k=1}^{K}\beta_{k}X_{ki}+\varepsilon_{i}$$`
the standard error for the `$kth$` sample slope, `$\beta_{k}$`, is:

`$$SE(\hat{\beta}_{k})=\frac{\sigma_{e}}{\sigma_{\tilde{X}_{k}}\sqrt{n-p}}$$`

where `$p$` is the number of parameters to be estimated, and `$\sigma_{\tilde{X}_{k}}$` is the standard deviation of `$\tilde{X}_{ki}$`, the residual from a regression of `$X_{ki}$` on all other regressors (remember the FWL theorem?). As you add more and more explanatory variables in the regression, `$\sigma_{e}$` will fall. On the other hand, the standard deviation of `$\sigma_{\tilde{X}_{k}}$` gets smaller since additional regressors might explain some variation of `$X_{ki}$`. The upshot of these changes in the top and bottom can be increased or decreased precision.

]

```r
options(scipen=999)
data("wage1", package = "wooldridge")   # load data

### Standard deviation of educ
sdX<-sd(wage1$educ)

### Number of observations in the sample
n<-nrow(wage1)

### Regression residuals
reg<-lm(lwage~educ, data=wage1)
sde<-sd(residuals(reg))

### Standard error of beta1
SE_educ<-sde/(sqrt(n-2)*sdX)
SE_educ
```

[1] 0.007566694

]

]
---

---

# Example: Private School Effects

* Students who attended a private four-year college in America paid an average of about $31,875 in tuition and fees in the 2018-19 period, while students who went to a public university in their home state paid, on average, 9,212 dollars - the yearly difference in tuition is considerable. Is it worth it?

* Comparisons between earnings of those who went to different schools may reveal a significant gap favoring elite-college alumni. Indeed, on average, the wage difference is **14% in favor of those who went private**. Is that a fair comparison?

* Differences in test scores, family background, motivation, and perhaps other skills and talents affect future earnings. Without dealing with *selection bias*, one cannot claim that there is a causal effect of private education on salaries

* What if we use regression to control for family income, SAT scores, and other covariates that we can observe?  
  
  * Still, there are factors complicated to quantify that might affect both attendance decisions and later earnings. For instance, how do we take into account diligence and family connections?
  
---
# Dale and Krueger (2002) I

* Instead of focusing on everything that might matter for college choice and earnings, Stacy Dale and Alan Krueger1 came up with a compelling shortcut: the characteristics of colleges to which students applied and were admitted

* Consider the case of two students who both applied to and were admitted to UMass and Harvard, but one goes to Harvard, and the other goes to UMass. The fact that those students applied to the same universities suggests they have similar ambition and motivation. Since both were admitted to the same places, one can assume that they might be able to succeed under the same circumstances. Hence, comparing earnings of those two similar students that took different paths would be fair

* Dale and Krueger analyzed a large data set called College and Beyond (C&B). The C&B data contains information about thousands of students who enrolled in a group of selective U.S. universities, together with survey information collected multiple times from the year students took the SAT to long after most had graduated from college

.footnote[ [1] Stacy Berg Dale and Alan B. Krueger, "Estimating the Payoff to Attending a More Selective College: An Application of Selection on Observables and Unobservables," *Quarterly Journal of Economics*, vol. 117, no. 4, November 2002.]

---

# College Matching Matrix I

.pull-left[ The table illustrates the idea of "college matching." There you have applications, admissions, and matriculation decisions for nine made-up students and six made-up universities.

What happens when we compare the earnings of those who entered private with those who went to public universities?

**Average earnings of Private university students:**
  
`$\frac{110,000+100,000+60,000+115,000+75,000}{5}=92,000$`

**Average earnings of Public university students:**

`$\frac{110,000+30,000+90,000+60,000}{4}=72,500$`

**That gap suggests a sizeable private school advantage.**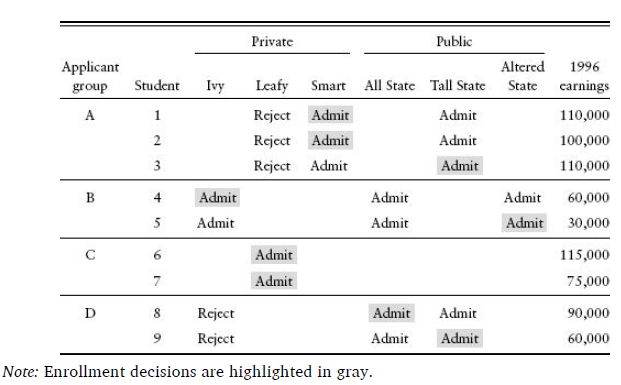

]

![](figs/fig1.png)

---

# College Matching Matrix II

The table organizes nine students into four groups. Each group is defined by the set of schools to which they **applied** and were **admitted**. Within each group, students are most likely similar in characteristics that are hard to quantify, such as ability and ambition.

Hence, within-group comparisons can be considered apples-to-apples comparisons. Since students in groups C and D attended only private and public schools, respectively, there is not much information there. Focusing only on groups A and B, the earnings gap between private and public education is

$$(\frac{3}{5} \times -5,000) + (\frac{2}{5}) \times 30,000=9,000 $$
where -5,000 and 30,000 are the private school differentials in groups A and B.

]

![](figs/fig1.png)

---

# Dale and Krueger (2002) II

Using the C&B dataset, Dale and Krueger matched 5,583 students into 151 similar selectivity groups containing students who went to both public and private universities. Besides the "group variables" that capture the relative selectivity of the schools to which students applied and were admitted, the researchers also controlled for other variables such as SAT scores and parental income.

The resulting regression model looks like this:

`$$ln(Earnings_{i})=\beta_{0}+\beta_{1}Private_{i}+
\sum_{j=1}^{150}\gamma_{j}GROUP_{ji}+\delta_{1}SAT_{i}+\delta_{2}PI_{i}+\varepsilon_{i}$$`

where `$\beta_{1}$` is the treatment effect of interest: the extent to which earnings differ for students who attend a private school compared to students who went to public universities. The model also controls for 151 selectivity groups: the variable `$GROUP_{ji}$` equals to one when student `$i$` is in the group `$j$` and is zero otherwise. **The idea is to control for the sets of schools to which students applied and were admitted** to bring the comparison as close as possible to an apples-to-apples comparison.

---

# Dale and Krueger (2002) III

* The table reports the results of six regressions. The first column captures the difference (in %) of earnings between those who attended a private school and everyone else: a pretty large difference (around 14%)

* Adding more and more controls that the researchers observe, there is still a gap around 9% (columns 2 and 3) - not as large as 14%, but still relevant

* However, when considering the selectivity-group dummies (columns 4 to 6), the gap shrinks and is not statistically significant anymore: the private school premium is gone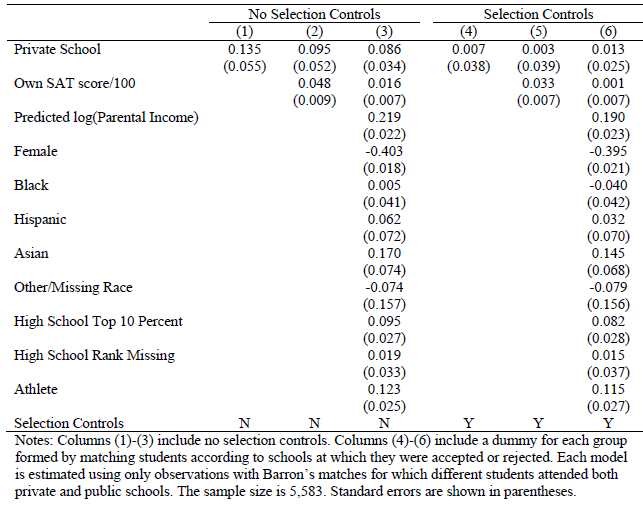

]

![](figs/fig2_2.png)
]

---
# Regression and Causality I

.center[Regression reduces - maybe even eliminates - selection bias **as long as you have credible identification strategy**]

Let's go back to our potential outcomes framework:
`$$Y_{i}=Y_{0i}+D_{i}(Y_{1i}-Y_{0i})$$`
where we get to see either `$Y_{1i}$` or `$Y_{0i}$`, but never both. We hope to measure the average `$Y_{1i}-Y_{0i}$`. The naive comparison gives us

.bg-washed-yellow.b--orange.ba.bw2.br3.shadow-5.ph4.mt1[
`\begin{equation*}
\underbrace{E[Y_{i} | D_{i}=1]-E[Y_{i} | D_{i}=0]}_{\text{Observed difference}}=
\underbrace{E[Y_{1i}|D_{i}=1]-E[Y_{0i}|D_{i}=1]}_{\text{Average treatment effect on the treated}}+\underbrace{E[Y_{0i}|D_{i}=1]-E[Y_{0i}|D_{i}=0]}_{\text{Selection bias}}
\end{equation*}`
]

In the example of private *versus* public education, students that go to private schools would have higher future earnings after college anyway, and the positive bias exacerbates the benefits of private education.

---
# Regression and Causality II

The **conditional independence assumption** (CIA) asserts that conditional on observed characteristics, `$X_{i}$`, the selection bias disappears. Formally,

`$$Y_{1i}, Y_{0i} \perp\!\!\!\perp D_{i}|X_{i}$$`

Given the CIA, `$conditional-on-X_{i}$` comparisons have a causal interpretation:

`$$E[Y_{i}|X_{i}, D_{i}=1]-E[Y_{i}|X_{i}, D_{i}=0]=E[Y_{1i}-Y_{0i}|X_{i}]$$`

Back to the private *versus* public education:

`$$E[Y_{0i}|Private_{i};GROUP_{i},SAT_{i}, lnPI_{i}]=E[Y_{0i}|GROUP_{i},SAT_{i}, lnPI_{i}]$$`
and the CIA makes this causal.

---

---

# OVB I

Regression is a way to make **other things equal**. However, you can only generate fair comparisons for variables included on the right-hand side - fail to include what matters still leaves us with selection bias. The "regression version" of selection bias is what we call **omitted variable bias (OVB)**. Let us go back to our example of earnings *versus* schooling. We already ran both the *long regression*

`$$\underbrace{Y_{i}}_{Wage_{i}}=\beta_{0}^{l}+\beta_{1}^{l}\underbrace{X_{1i}}_{Educ_{i}}+\beta_{2}\underbrace{X_{2i}}_{Exper_{i}}+\varepsilon_{i}^{l}$$`
and the *short regression*

`$$\underbrace{Y_{i}}_{Wage_{i}}=\beta_{0}^{s}+\beta_{1}^{s}\underbrace{X_{1i}}_{Educ_{i}}+\varepsilon_{i}^{s}$$`

The OVB formula describes the relationship between short and long coefficients as follows:

`$$\beta^{s}=\beta^{l}+\pi_{21} \beta_{2}$$`

where `$\beta_{2}$` is the coefficient is the coefficient of `$X_{2i}$` in the long regression, and `$\pi_{21}$` is the coefficient of `$X_{1i}$` in a regression of `$X_{2i}$` on `$X_{1i}$`.

---

# OVB II

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.083*** (0.008)</td></tr>
<tr><td style="text-align:left">Constant</td><td>0.584*** (0.097)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.184</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>

]

<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Hourly Wages</td></tr>
<tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">educ</td><td>0.098*** (0.008)</td></tr>
<tr><td style="text-align:left">exper</td><td>0.010*** (0.002)</td></tr>
<tr><td style="text-align:left">Constant</td><td>0.217** (0.109)</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>526</td></tr>
<tr><td style="text-align:left">Adjusted R2</td><td>0.246</td></tr>
<tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Note:</td><td style="text-align:right">*p<0.1; **p<0.05; ***p<0.01</td></tr>
</table>

]

```r
library(wooldridge)
# load data
data("wage1", package = "wooldridge")

short_reg<-lm(lwage~educ, data=wage1)
beta_short<-short_reg$coefficients[2]
beta_short
```

educ 
0.08274437

]

```r
long_reg<-lm(lwage~educ+exper, data=wage1)
beta_long<-long_reg$coefficients[2]
beta2<-long_reg$coefficients[3]

exper_on_educ<-lm(exper~educ, data=wage1)
pi12<-exper_on_educ$coefficients[2]

beta_long+pi12*beta2 
```

educ 
0.08274437

```r
## which is equal to beta_short
```
]

]

---
# OVB III

In other words, the omitted variable bias (OVB) formula connects regression coefficients in models with different controls. Consider the following **long regression** of wages on schooling `$(s_{i})$`, controlling for ability `$(A_{i})$`:

`$$Y_{i} = \alpha+\rho s_{i}+ A^{'}_{i} \gamma + \varepsilon_{i}$$`
Since ability is hard to measure, what are the consequences of omitting that variable?

`$$\dfrac{Cov(Y_{i}, s_{i})}{V(s_{i})}=\rho+\gamma^{'}\delta_{As}$$`
where `$\delta_{As}$` is the vector of coefficients from regressions of the elements of `$A_{i}$` on `$s_{i}$`.

In English, *short equals long plus the effect of omitted times the regression of omitted on included*. **When omitted and included are uncorrelated, short `$=$` long.**

---
# Regression Sensitivity Analysis

* We are never sure whether a given set of controls is enough to eliminate selection bias. However, we may ask one important question: how sensitive are regression results to changes in the control variables?

* Usually, our confidence in regression estimates of causal effects grows when treatment effects are insensitive to whether a particular variable is included or not in the model as long as a few core controls are always included in the model

* Back to Dale and Krueger (2002), you can see that after they take into account the selectivity-group dummies (columns 4 to 6), the effect of private education remains the same even after the inclusion of multiple covariates

]

![](figs/fig2_2.png)
]

---

---

# Your Standard Errors are Probably Wrong

.pull-left[
* We saw that our regression estimates are subject to sampling variation, and we need to account for that uncertainty estimating the standard error `$SE(\hat{\beta}_{k})$`. With that estimate, one can calculate test statistics to evaluate statistical significance, confidence intervals, etc.

* Standard errors computed using `$SE(\hat{\beta}_{k})=\frac{\sigma_{e}}{\sigma_{\tilde{X}_{k}}\sqrt{n-p}}$` are nowadays considered old-fashioned because that formula is derived assuming the variance of residuals is unrelated to regressors - the *homoskedasticity* assumption

* Most of the time, that is a heroic assumption. For instance, you can see that among people with higher levels of education (10 years +), salary varies a lot more compared to individuals with fewer years of education

]

<div id="htmlwidget-1431e8abb6c5c58ab250" style="width:560px;height:430px;" class="plotly html-widget"></div>
<script type="application/json" data-for="htmlwidget-1431e8abb6c5c58ab250">{"x":{"data":[{"x":[11,12,11,8,12,16,18,12,12,17,16,13,12,12,12,16,12,13,12,12,12,12,16,12,11,16,16,16,15,8,14,14,13,12,12,16,12,4,14,12,12,12,14,11,13,15,10,12,14,12,12,16,12,12,12,15,16,8,18,16,13,14,10,10,14,14,16,12,16,12,16,17,12,12,12,13,12,12,12,18,9,16,10,12,12,12,12,12,8,12,12,14,12,12,12,9,13,12,14,12,15,12,12,12,14,15,12,12,12,17,11,18,12,14,14,10,14,12,15,8,16,14,15,12,18,16,10,8,10,11,18,15,12,11,12,12,14,16,2,14,16,12,12,13,12,15,10,12,16,13,9,12,13,12,12,14,16,16,9,18,10,10,13,12,18,13,12,13,13,13,18,12,12,13,12,12,12,14,10,12,16,16,12,14,12,12,12,12,12,12,12,16,16,14,11,16,12,12,17,12,12,16,8,12,12,12,16,12,12,9,13,16,14,8,14,13,12,18,9,8,8,12,14,12,16,8,13,9,16,12,15,11,14,12,12,12,18,12,12,12,12,12,12,14,16,12,14,11,12,10,12,6,13,12,10,12,14,13,12,18,12,12,12,12,12,8,13,13,14,12,10,16,12,16,12,14,18,17,13,14,15,14,12,8,12,12,8,12,9,12,16,12,16,12,12,13,10,6,12,12,16,12,8,12,6,4,11,11,7,12,18,12,16,12,14,12,10,10,9,10,12,12,12,10,16,16,16,12,12,7,8,16,16,18,13,10,16,14,16,12,9,11,11,12,11,12,12,12,12,14,14,18,12,12,12,11,12,17,16,13,13,12,14,14,11,10,8,14,12,10,17,9,12,12,14,16,12,10,0,14,15,16,12,11,11,12,13,12,13,16,15,16,15,12,18,6,6,12,12,16,9,12,11,10,12,8,9,17,16,11,10,8,13,14,13,11,7,16,12,13,14,16,14,11,8,14,17,10,12,12,18,14,18,12,16,14,12,9,12,12,17,12,15,17,16,12,15,16,12,15,12,12,12,12,16,11,14,14,13,14,12,12,8,12,3,11,15,11,12,4,9,12,12,11,12,16,13,15,16,12,12,12,9,10,12,11,8,6,16,12,12,16,12,10,13,13,14,16,10,12,12,11,0,5,16,16,9,15,12,12,12,13,12,7,17,12,12,14,12,13,12,16,10,15,16,14],"y":[3.09999990463257,3.24000000953674,3,6,5.30000019073486,8.75,11.25,5,3.59999990463257,18.1800003051758,6.25,8.13000011444092,8.77000045776367,5.5,22.2000007629395,17.3299999237061,7.5,10.6300001144409,3.59999990463257,4.5,6.88000011444092,8.47999954223633,6.32999992370605,0.529999971389771,6,9.5600004196167,7.78000020980835,12.5,12.5,3.25,13,4.5,9.68000030517578,5,4.67999982833862,4.26999998092651,6.15000009536743,3.50999999046326,3,6.25,7.80999994277954,10,4.5,4,6.38000011444092,13.6999998092651,1.66999995708466,2.9300000667572,3.65000009536743,2.90000009536743,1.62999999523163,8.60000038146973,5,6,2.5,3.25,3.40000009536743,10,21.6299991607666,4.38000011444092,11.710000038147,12.3900003433228,6.25,3.71000003814697,7.78000020980835,19.9799995422363,6.25,10,5.71000003814697,2,5.71000003814697,13.0799999237061,4.90999984741211,2.91000008583069,3.75,11.8999996185303,4,3.09999990463257,8.44999980926514,7.1399998664856,4.5,4.65000009536743,2.90000009536743,6.67000007629395,3.5,3.25999999046326,3.25,8,9.85000038146973,7.5,5.90999984741211,11.7600002288818,3,4.80999994277954,6.5,4,3.5,13.1599998474121,4.25,3.5,5.13000011444092,3.75,4.5,7.63000011444092,15,6.84999990463257,13.3299999237061,6.67000007629395,2.52999997138977,9.80000019073486,3.36999988555908,24.9799995422363,5.40000009536743,6.1100001335144,4.19999980926514,3.75,3.5,3.64000010490417,3.79999995231628,3,5,4.63000011444092,3,3.20000004768372,3.91000008583069,6.42999982833862,5.48000001907349,1.5,2.90000009536743,5,8.92000007629395,5,3.51999998092651,2.90000009536743,4.5,2.25,5,10,3.75,10,10.9499998092651,7.90000009536743,4.71999979019165,5.84000015258789,3.82999992370605,3.20000004768372,2,4.5,11.5500001907349,2.14000010490417,2.38000011444092,3.75,5.51999998092651,6.5,3.09999990463257,10,6.63000011444092,10,2.30999994277954,6.88000011444092,2.82999992370605,3.13000011444092,8,4.5,8.64999961853027,2,4.75,6.25,6,15.3800001144409,14.5799999237061,12.5,5.25,2.17000007629395,7.1399998664856,6.21999979019165,9,10,5.76999998092651,4,8.75,6.53000020980835,7.59999990463257,5,5,21.8600006103516,8.64000034332275,3.29999995231628,4.44000005722046,4.55000019073486,3.5,6.25,3.84999990463257,6.17999982833862,2.91000008583069,6.25,6.25,9.05000019073486,10,11.1099996566772,6.88000011444092,8.75,10,3.04999995231628,3,5.80000019073486,4.09999990463257,8,6.15000009536743,2.70000004768372,2.75,3,3,7.3600001335144,7.5,3.5,8.10000038146973,3.75,3.25,5.82999992370605,3.5,3.32999992370605,4,3.5,6.25,2.95000004768372,5.71000003814697,3,22.8600006103516,9,8.32999992370605,3,5.75,6.76000022888184,10,3,3.5,3.25,4,2.92000007629395,3.05999994277954,3.20000004768372,4.75,3,18.1599998474121,3.5,4.1100001335144,1.96000003814697,4.28999996185303,3,6.44999980926514,5.19999980926514,4.5,3.88000011444092,3.45000004768372,10.9099998474121,4.09999990463257,3,5.90000009536743,18,4,3,3.54999995231628,3,8.75,2.90000009536743,6.26000022888184,3.5,4.59999990463257,6,2.89000010490417,5.57999992370605,4,6,4.5,2.92000007629395,4.32999992370605,18.8899993896484,4.28000020980835,4.57000017166138,6.25,2.95000004768372,8.75,8.5,3.75,3.15000009536743,5,6.46000003814697,2,4.78999996185303,5.78000020980835,3.1800000667572,4.67999982833862,4.09999990463257,2.91000008583069,6,3.59999990463257,3.95000004768372,7,3,6.07999992370605,8.63000011444092,3,3.75,2.90000009536743,3,6.25,3.5,3,3.24000000953674,8.02000045776367,3.32999992370605,5.25,6.25,3.5,2.95000004768372,3,4.69000005722046,3.73000001907349,4,4,2.90000009536743,3.04999995231628,5.05000019073486,13.9499998092651,18.1599998474121,6.25,5.25,4.78999996185303,3.34999990463257,3,8.43000030517578,5.69999980926514,11.9799995422363,3.5,4.23999977111816,7,6,12.2200002670288,4.5,3,2.90000009536743,15,4,5.25,4,3.29999995231628,5.05000019073486,3.57999992370605,5,4.57000017166138,12.5,3.45000004768372,4.63000011444092,10,2.92000007629395,4.51000022888184,6.5,7.5,3.53999996185303,4.19999980926514,3.50999999046326,4.5,3.34999990463257,2.91000008583069,5.25,4.05000019073486,3.75,3.40000009536743,3,6.28999996185303,2.53999996185303,4.5,3.13000011444092,6.3600001335144,4.67999982833862,6.80000019073486,8.52999973297119,4.17000007629395,3.75,11.1000003814697,3.25999999046326,9.13000011444092,4.5,3,8.75,4.1399998664856,2.86999988555908,3.34999990463257,6.07999992370605,3,4.19999980926514,5.59999990463257,10,12.5,3.75999999046326,3.09999990463257,4.28999996185303,10.9200000762939,7.5,4.05000019073486,4.65000009536743,5,2.90000009536743,8,8.43000030517578,2.92000007629395,6.25,6.25,5.1100001335144,4,4.44000005722046,6.88000011444092,5.42999982833862,3,2.90000009536743,6.25,4.34000015258789,3.25,7.26000022888184,6.34999990463257,5.63000011444092,8.75,3.20000004768372,3,3,12.5,2.88000011444092,3.34999990463257,6.5,10.3800001144409,4.5,10,3.80999994277954,8.80000019073486,9.42000007629395,6.32999992370605,4,2.90000009536743,20,11.25,3.5,6,14.3800001144409,6.3600001335144,3.54999995231628,3,4.5,6.63000011444092,9.30000019073486,3,3.25,1.5,5.90000009536743,8,2.90000009536743,3.28999996185303,6.5,4,6,4.07999992370605,3.75,3.04999995231628,3.5,2.92000007629395,4.5,3.34999990463257,5.94999980926514,8,3,5,5.5,2.65000009536743,3,4.5,17.5,8.18000030517578,9.09000015258789,11.8199996948242,3.25,4.5,4.5,3.71000003814697,6.5,2.90000009536743,5.59999990463257,2.23000001907349,5,8.32999992370605,2.90000009536743,6.25,4.55000019073486,3.27999997138977,2.29999995231628,3.29999995231628,3.15000009536743,12.5,5.15000009536743,3.13000011444092,7.25,2.90000009536743,1.75,2.89000010490417,2.90000009536743,17.7099990844727,6.25,2.59999990463257,6.63000011444092,3.5,6.5,3,4.38000011444092,10,4.94999980926514,9,1.42999994754791,3.07999992370605,9.32999992370605,7.5,4.75,5.65000009536743,15,2.26999998092651,4.67000007629395,11.5600004196167,3.5],"text":["educ: 11 wage: 3.10","educ: 12 wage: 3.24","educ: 11 wage: 3.00","educ: 8 wage: 6.00","educ: 12 wage: 5.30","educ: 16 wage: 8.75","educ: 18 wage: 11.25","educ: 12 wage: 5.00","educ: 12 wage: 3.60","educ: 17 wage: 18.18","educ: 16 wage: 6.25","educ: 13 wage: 8.13","educ: 12 wage: 8.77","educ: 12 wage: 5.50","educ: 12 wage: 22.20","educ: 16 wage: 17.33","educ: 12 wage: 7.50","educ: 13 wage: 10.63","educ: 12 wage: 3.60","educ: 12 wage: 4.50","educ: 12 wage: 6.88","educ: 12 wage: 8.48","educ: 16 wage: 6.33","educ: 12 wage: 0.53","educ: 11 wage: 6.00","educ: 16 wage: 9.56","educ: 16 wage: 7.78","educ: 16 wage: 12.50","educ: 15 wage: 12.50","educ: 8 wage: 3.25","educ: 14 wage: 13.00","educ: 14 wage: 4.50","educ: 13 wage: 9.68","educ: 12 wage: 5.00","educ: 12 wage: 4.68","educ: 16 wage: 4.27","educ: 12 wage: 6.15","educ: 4 wage: 3.51","educ: 14 wage: 3.00","educ: 12 wage: 6.25","educ: 12 wage: 7.81","educ: 12 wage: 10.00","educ: 14 wage: 4.50","educ: 11 wage: 4.00","educ: 13 wage: 6.38","educ: 15 wage: 13.70","educ: 10 wage: 1.67","educ: 12 wage: 2.93","educ: 14 wage: 3.65","educ: 12 wage: 2.90","educ: 12 wage: 1.63","educ: 16 wage: 8.60","educ: 12 wage: 5.00","educ: 12 wage: 6.00","educ: 12 wage: 2.50","educ: 15 wage: 3.25","educ: 16 wage: 3.40","educ: 8 wage: 10.00","educ: 18 wage: 21.63","educ: 16 wage: 4.38","educ: 13 wage: 11.71","educ: 14 wage: 12.39","educ: 10 wage: 6.25","educ: 10 wage: 3.71","educ: 14 wage: 7.78","educ: 14 wage: 19.98","educ: 16 wage: 6.25","educ: 12 wage: 10.00","educ: 16 wage: 5.71","educ: 12 wage: 2.00","educ: 16 wage: 5.71","educ: 17 wage: 13.08","educ: 12 wage: 4.91","educ: 12 wage: 2.91","educ: 12 wage: 3.75","educ: 13 wage: 11.90","educ: 12 wage: 4.00","educ: 12 wage: 3.10","educ: 12 wage: 8.45","educ: 18 wage: 7.14","educ: 9 wage: 4.50","educ: 16 wage: 4.65","educ: 10 wage: 2.90","educ: 12 wage: 6.67","educ: 12 wage: 3.50","educ: 12 wage: 3.26","educ: 12 wage: 3.25","educ: 12 wage: 8.00","educ: 8 wage: 9.85","educ: 12 wage: 7.50","educ: 12 wage: 5.91","educ: 14 wage: 11.76","educ: 12 wage: 3.00","educ: 12 wage: 4.81","educ: 12 wage: 6.50","educ: 9 wage: 4.00","educ: 13 wage: 3.50","educ: 12 wage: 13.16","educ: 14 wage: 4.25","educ: 12 wage: 3.50","educ: 15 wage: 5.13","educ: 12 wage: 3.75","educ: 12 wage: 4.50","educ: 12 wage: 7.63","educ: 14 wage: 15.00","educ: 15 wage: 6.85","educ: 12 wage: 13.33","educ: 12 wage: 6.67","educ: 12 wage: 2.53","educ: 17 wage: 9.80","educ: 11 wage: 3.37","educ: 18 wage: 24.98","educ: 12 wage: 5.40","educ: 14 wage: 6.11","educ: 14 wage: 4.20","educ: 10 wage: 3.75","educ: 14 wage: 3.50","educ: 12 wage: 3.64","educ: 15 wage: 3.80","educ: 8 wage: 3.00","educ: 16 wage: 5.00","educ: 14 wage: 4.63","educ: 15 wage: 3.00","educ: 12 wage: 3.20","educ: 18 wage: 3.91","educ: 16 wage: 6.43","educ: 10 wage: 5.48","educ: 8 wage: 1.50","educ: 10 wage: 2.90","educ: 11 wage: 5.00","educ: 18 wage: 8.92","educ: 15 wage: 5.00","educ: 12 wage: 3.52","educ: 11 wage: 2.90","educ: 12 wage: 4.50","educ: 12 wage: 2.25","educ: 14 wage: 5.00","educ: 16 wage: 10.00","educ: 2 wage: 3.75","educ: 14 wage: 10.00","educ: 16 wage: 10.95","educ: 12 wage: 7.90","educ: 12 wage: 4.72","educ: 13 wage: 5.84","educ: 12 wage: 3.83","educ: 15 wage: 3.20","educ: 10 wage: 2.00","educ: 12 wage: 4.50","educ: 16 wage: 11.55","educ: 13 wage: 2.14","educ: 9 wage: 2.38","educ: 12 wage: 3.75","educ: 13 wage: 5.52","educ: 12 wage: 6.50","educ: 12 wage: 3.10","educ: 14 wage: 10.00","educ: 16 wage: 6.63","educ: 16 wage: 10.00","educ: 9 wage: 2.31","educ: 18 wage: 6.88","educ: 10 wage: 2.83","educ: 10 wage: 3.13","educ: 13 wage: 8.00","educ: 12 wage: 4.50","educ: 18 wage: 8.65","educ: 13 wage: 2.00","educ: 12 wage: 4.75","educ: 13 wage: 6.25","educ: 13 wage: 6.00","educ: 13 wage: 15.38","educ: 18 wage: 14.58","educ: 12 wage: 12.50","educ: 12 wage: 5.25","educ: 13 wage: 2.17","educ: 12 wage: 7.14","educ: 12 wage: 6.22","educ: 12 wage: 9.00","educ: 14 wage: 10.00","educ: 10 wage: 5.77","educ: 12 wage: 4.00","educ: 16 wage: 8.75","educ: 16 wage: 6.53","educ: 12 wage: 7.60","educ: 14 wage: 5.00","educ: 12 wage: 5.00","educ: 12 wage: 21.86","educ: 12 wage: 8.64","educ: 12 wage: 3.30","educ: 12 wage: 4.44","educ: 12 wage: 4.55","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 16 wage: 3.85","educ: 14 wage: 6.18","educ: 11 wage: 2.91","educ: 16 wage: 6.25","educ: 12 wage: 6.25","educ: 12 wage: 9.05","educ: 17 wage: 10.00","educ: 12 wage: 11.11","educ: 12 wage: 6.88","educ: 16 wage: 8.75","educ: 8 wage: 10.00","educ: 12 wage: 3.05","educ: 12 wage: 3.00","educ: 12 wage: 5.80","educ: 16 wage: 4.10","educ: 12 wage: 8.00","educ: 12 wage: 6.15","educ: 9 wage: 2.70","educ: 13 wage: 2.75","educ: 16 wage: 3.00","educ: 14 wage: 3.00","educ: 8 wage: 7.36","educ: 14 wage: 7.50","educ: 13 wage: 3.50","educ: 12 wage: 8.10","educ: 18 wage: 3.75","educ: 9 wage: 3.25","educ: 8 wage: 5.83","educ: 8 wage: 3.50","educ: 12 wage: 3.33","educ: 14 wage: 4.00","educ: 12 wage: 3.50","educ: 16 wage: 6.25","educ: 8 wage: 2.95","educ: 13 wage: 5.71","educ: 9 wage: 3.00","educ: 16 wage: 22.86","educ: 12 wage: 9.00","educ: 15 wage: 8.33","educ: 11 wage: 3.00","educ: 14 wage: 5.75","educ: 12 wage: 6.76","educ: 12 wage: 10.00","educ: 12 wage: 3.00","educ: 18 wage: 3.50","educ: 12 wage: 3.25","educ: 12 wage: 4.00","educ: 12 wage: 2.92","educ: 12 wage: 3.06","educ: 12 wage: 3.20","educ: 12 wage: 4.75","educ: 14 wage: 3.00","educ: 16 wage: 18.16","educ: 12 wage: 3.50","educ: 14 wage: 4.11","educ: 11 wage: 1.96","educ: 12 wage: 4.29","educ: 10 wage: 3.00","educ: 12 wage: 6.45","educ: 6 wage: 5.20","educ: 13 wage: 4.50","educ: 12 wage: 3.88","educ: 10 wage: 3.45","educ: 12 wage: 10.91","educ: 14 wage: 4.10","educ: 13 wage: 3.00","educ: 12 wage: 5.90","educ: 18 wage: 18.00","educ: 12 wage: 4.00","educ: 12 wage: 3.00","educ: 12 wage: 3.55","educ: 12 wage: 3.00","educ: 12 wage: 8.75","educ: 8 wage: 2.90","educ: 13 wage: 6.26","educ: 13 wage: 3.50","educ: 14 wage: 4.60","educ: 12 wage: 6.00","educ: 10 wage: 2.89","educ: 16 wage: 5.58","educ: 12 wage: 4.00","educ: 16 wage: 6.00","educ: 12 wage: 4.50","educ: 14 wage: 2.92","educ: 18 wage: 4.33","educ: 17 wage: 18.89","educ: 13 wage: 4.28","educ: 14 wage: 4.57","educ: 15 wage: 6.25","educ: 14 wage: 2.95","educ: 12 wage: 8.75","educ: 8 wage: 8.50","educ: 12 wage: 3.75","educ: 12 wage: 3.15","educ: 8 wage: 5.00","educ: 12 wage: 6.46","educ: 9 wage: 2.00","educ: 12 wage: 4.79","educ: 16 wage: 5.78","educ: 12 wage: 3.18","educ: 16 wage: 4.68","educ: 12 wage: 4.10","educ: 12 wage: 2.91","educ: 13 wage: 6.00","educ: 10 wage: 3.60","educ: 6 wage: 3.95","educ: 12 wage: 7.00","educ: 12 wage: 3.00","educ: 16 wage: 6.08","educ: 12 wage: 8.63","educ: 8 wage: 3.00","educ: 12 wage: 3.75","educ: 6 wage: 2.90","educ: 4 wage: 3.00","educ: 11 wage: 6.25","educ: 11 wage: 3.50","educ: 7 wage: 3.00","educ: 12 wage: 3.24","educ: 18 wage: 8.02","educ: 12 wage: 3.33","educ: 16 wage: 5.25","educ: 12 wage: 6.25","educ: 14 wage: 3.50","educ: 12 wage: 2.95","educ: 10 wage: 3.00","educ: 10 wage: 4.69","educ: 9 wage: 3.73","educ: 10 wage: 4.00","educ: 12 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 3.05","educ: 10 wage: 5.05","educ: 16 wage: 13.95","educ: 16 wage: 18.16","educ: 16 wage: 6.25","educ: 12 wage: 5.25","educ: 12 wage: 4.79","educ: 7 wage: 3.35","educ: 8 wage: 3.00","educ: 16 wage: 8.43","educ: 16 wage: 5.70","educ: 18 wage: 11.98","educ: 13 wage: 3.50","educ: 10 wage: 4.24","educ: 16 wage: 7.00","educ: 14 wage: 6.00","educ: 16 wage: 12.22","educ: 12 wage: 4.50","educ: 9 wage: 3.00","educ: 11 wage: 2.90","educ: 11 wage: 15.00","educ: 12 wage: 4.00","educ: 11 wage: 5.25","educ: 12 wage: 4.00","educ: 12 wage: 3.30","educ: 12 wage: 5.05","educ: 12 wage: 3.58","educ: 14 wage: 5.00","educ: 14 wage: 4.57","educ: 18 wage: 12.50","educ: 12 wage: 3.45","educ: 12 wage: 4.63","educ: 12 wage: 10.00","educ: 11 wage: 2.92","educ: 12 wage: 4.51","educ: 17 wage: 6.50","educ: 16 wage: 7.50","educ: 13 wage: 3.54","educ: 13 wage: 4.20","educ: 12 wage: 3.51","educ: 14 wage: 4.50","educ: 14 wage: 3.35","educ: 11 wage: 2.91","educ: 10 wage: 5.25","educ: 8 wage: 4.05","educ: 14 wage: 3.75","educ: 12 wage: 3.40","educ: 10 wage: 3.00","educ: 17 wage: 6.29","educ: 9 wage: 2.54","educ: 12 wage: 4.50","educ: 12 wage: 3.13","educ: 14 wage: 6.36","educ: 16 wage: 4.68","educ: 12 wage: 6.80","educ: 10 wage: 8.53","educ: 0 wage: 4.17","educ: 14 wage: 3.75","educ: 15 wage: 11.10","educ: 16 wage: 3.26","educ: 12 wage: 9.13","educ: 11 wage: 4.50","educ: 11 wage: 3.00","educ: 12 wage: 8.75","educ: 13 wage: 4.14","educ: 12 wage: 2.87","educ: 13 wage: 3.35","educ: 16 wage: 6.08","educ: 15 wage: 3.00","educ: 16 wage: 4.20","educ: 15 wage: 5.60","educ: 12 wage: 10.00","educ: 18 wage: 12.50","educ: 6 wage: 3.76","educ: 6 wage: 3.10","educ: 12 wage: 4.29","educ: 12 wage: 10.92","educ: 16 wage: 7.50","educ: 9 wage: 4.05","educ: 12 wage: 4.65","educ: 11 wage: 5.00","educ: 10 wage: 2.90","educ: 12 wage: 8.00","educ: 8 wage: 8.43","educ: 9 wage: 2.92","educ: 17 wage: 6.25","educ: 16 wage: 6.25","educ: 11 wage: 5.11","educ: 10 wage: 4.00","educ: 8 wage: 4.44","educ: 13 wage: 6.88","educ: 14 wage: 5.43","educ: 13 wage: 3.00","educ: 11 wage: 2.90","educ: 7 wage: 6.25","educ: 16 wage: 4.34","educ: 12 wage: 3.25","educ: 13 wage: 7.26","educ: 14 wage: 6.35","educ: 16 wage: 5.63","educ: 14 wage: 8.75","educ: 11 wage: 3.20","educ: 8 wage: 3.00","educ: 14 wage: 3.00","educ: 17 wage: 12.50","educ: 10 wage: 2.88","educ: 12 wage: 3.35","educ: 12 wage: 6.50","educ: 18 wage: 10.38","educ: 14 wage: 4.50","educ: 18 wage: 10.00","educ: 12 wage: 3.81","educ: 16 wage: 8.80","educ: 14 wage: 9.42","educ: 12 wage: 6.33","educ: 9 wage: 4.00","educ: 12 wage: 2.90","educ: 12 wage: 20.00","educ: 17 wage: 11.25","educ: 12 wage: 3.50","educ: 15 wage: 6.00","educ: 17 wage: 14.38","educ: 16 wage: 6.36","educ: 12 wage: 3.55","educ: 15 wage: 3.00","educ: 16 wage: 4.50","educ: 12 wage: 6.63","educ: 15 wage: 9.30","educ: 12 wage: 3.00","educ: 12 wage: 3.25","educ: 12 wage: 1.50","educ: 12 wage: 5.90","educ: 16 wage: 8.00","educ: 11 wage: 2.90","educ: 14 wage: 3.29","educ: 14 wage: 6.50","educ: 13 wage: 4.00","educ: 14 wage: 6.00","educ: 12 wage: 4.08","educ: 12 wage: 3.75","educ: 8 wage: 3.05","educ: 12 wage: 3.50","educ: 3 wage: 2.92","educ: 11 wage: 4.50","educ: 15 wage: 3.35","educ: 11 wage: 5.95","educ: 12 wage: 8.00","educ: 4 wage: 3.00","educ: 9 wage: 5.00","educ: 12 wage: 5.50","educ: 12 wage: 2.65","educ: 11 wage: 3.00","educ: 12 wage: 4.50","educ: 16 wage: 17.50","educ: 13 wage: 8.18","educ: 15 wage: 9.09","educ: 16 wage: 11.82","educ: 12 wage: 3.25","educ: 12 wage: 4.50","educ: 12 wage: 4.50","educ: 9 wage: 3.71","educ: 10 wage: 6.50","educ: 12 wage: 2.90","educ: 11 wage: 5.60","educ: 8 wage: 2.23","educ: 6 wage: 5.00","educ: 16 wage: 8.33","educ: 12 wage: 2.90","educ: 12 wage: 6.25","educ: 16 wage: 4.55","educ: 12 wage: 3.28","educ: 10 wage: 2.30","educ: 13 wage: 3.30","educ: 13 wage: 3.15","educ: 14 wage: 12.50","educ: 16 wage: 5.15","educ: 10 wage: 3.13","educ: 12 wage: 7.25","educ: 12 wage: 2.90","educ: 11 wage: 1.75","educ: 0 wage: 2.89","educ: 5 wage: 2.90","educ: 16 wage: 17.71","educ: 16 wage: 6.25","educ: 9 wage: 2.60","educ: 15 wage: 6.63","educ: 12 wage: 3.50","educ: 12 wage: 6.50","educ: 12 wage: 3.00","educ: 13 wage: 4.38","educ: 12 wage: 10.00","educ: 7 wage: 4.95","educ: 17 wage: 9.00","educ: 12 wage: 1.43","educ: 12 wage: 3.08","educ: 14 wage: 9.33","educ: 12 wage: 7.50","educ: 13 wage: 4.75","educ: 12 wage: 5.65","educ: 16 wage: 15.00","educ: 10 wage: 2.27","educ: 15 wage: 4.67","educ: 16 wage: 11.56","educ: 14 wage: 3.50"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(145,184,189,1)","opacity":1,"size":5.66929133858268,"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(145,184,189,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[0,0.227848101265823,0.455696202531646,0.683544303797468,0.911392405063291,1.13924050632911,1.36708860759494,1.59493670886076,1.82278481012658,2.0506329113924,2.27848101265823,2.50632911392405,2.73417721518987,2.9620253164557,3.18987341772152,3.41772151898734,3.64556962025316,3.87341772151899,4.10126582278481,4.32911392405063,4.55696202531646,4.78481012658228,5.0126582278481,5.24050632911392,5.46835443037975,5.69620253164557,5.92405063291139,6.15189873417722,6.37974683544304,6.60759493670886,6.83544303797468,7.06329113924051,7.29113924050633,7.51898734177215,7.74683544303797,7.9746835443038,8.20253164556962,8.43037974683544,8.65822784810127,8.88607594936709,9.11392405063291,9.34177215189873,9.56962025316456,9.79746835443038,10.0253164556962,10.253164556962,10.4810126582278,10.7088607594937,10.9367088607595,11.1645569620253,11.3924050632911,11.620253164557,11.8481012658228,12.0759493670886,12.3037974683544,12.5316455696203,12.7594936708861,12.9873417721519,13.2151898734177,13.4430379746835,13.6708860759494,13.8987341772152,14.126582278481,14.3544303797468,14.5822784810127,14.8101265822785,15.0379746835443,15.2658227848101,15.4936708860759,15.7215189873418,15.9493670886076,16.1772151898734,16.4050632911392,16.6329113924051,16.8607594936709,17.0886075949367,17.3164556962025,17.5443037974684,17.7721518987342,18],"y":[-0.904851611957259,-0.781503933679118,-0.658156255400976,-0.534808577122835,-0.411460898844693,-0.288113220566552,-0.16476554228841,-0.0414178640102687,0.0819298142678727,0.205277492546014,0.328625170824156,0.451972849102297,0.575320527380439,0.69866820565858,0.822015883936722,0.945363562214863,1.068711240493,1.19205891877115,1.31540659704929,1.43875427532743,1.56210195360557,1.68544963188371,1.80879731016185,1.93214498844,2.05549266671814,2.17884034499628,2.30218802327442,2.42553570155256,2.5488833798307,2.67223105810884,2.79557873638699,2.91892641466513,3.04227409294327,3.16562177122141,3.28896944949955,3.41231712777769,3.53566480605583,3.65901248433398,3.78236016261212,3.90570784089026,4.0290555191684,4.15240319744654,4.27575087572468,4.39909855400282,4.52244623228097,4.64579391055911,4.76914158883725,4.89248926711539,5.01583694539353,5.13918462367167,5.26253230194982,5.38587998022796,5.5092276585061,5.63257533678424,5.75592301506238,5.87927069334052,6.00261837161866,6.12596604989681,6.24931372817495,6.37266140645309,6.49600908473123,6.61935676300937,6.74270444128751,6.86605211956565,6.9893997978438,7.11274747612194,7.23609515440008,7.35944283267822,7.48279051095636,7.6061381892345,7.72948586751265,7.85283354579079,7.97618122406893,8.09952890234707,8.22287658062521,8.34622425890335,8.46957193718149,8.59291961545964,8.71626729373778,8.83961497201592],"text":["educ: 0.0000000 wage: -0.90485161","educ: 0.2278481 wage: -0.78150393","educ: 0.4556962 wage: -0.65815626","educ: 0.6835443 wage: -0.53480858","educ: 0.9113924 wage: -0.41146090","educ: 1.1392405 wage: -0.28811322","educ: 1.3670886 wage: -0.16476554","educ: 1.5949367 wage: -0.04141786","educ: 1.8227848 wage: 0.08192981","educ: 2.0506329 wage: 0.20527749","educ: 2.2784810 wage: 0.32862517","educ: 2.5063291 wage: 0.45197285","educ: 2.7341772 wage: 0.57532053","educ: 2.9620253 wage: 0.69866821","educ: 3.1898734 wage: 0.82201588","educ: 3.4177215 wage: 0.94536356","educ: 3.6455696 wage: 1.06871124","educ: 3.8734177 wage: 1.19205892","educ: 4.1012658 wage: 1.31540660","educ: 4.3291139 wage: 1.43875428","educ: 4.5569620 wage: 1.56210195","educ: 4.7848101 wage: 1.68544963","educ: 5.0126582 wage: 1.80879731","educ: 5.2405063 wage: 1.93214499","educ: 5.4683544 wage: 2.05549267","educ: 5.6962025 wage: 2.17884034","educ: 5.9240506 wage: 2.30218802","educ: 6.1518987 wage: 2.42553570","educ: 6.3797468 wage: 2.54888338","educ: 6.6075949 wage: 2.67223106","educ: 6.8354430 wage: 2.79557874","educ: 7.0632911 wage: 2.91892641","educ: 7.2911392 wage: 3.04227409","educ: 7.5189873 wage: 3.16562177","educ: 7.7468354 wage: 3.28896945","educ: 7.9746835 wage: 3.41231713","educ: 8.2025316 wage: 3.53566481","educ: 8.4303797 wage: 3.65901248","educ: 8.6582278 wage: 3.78236016","educ: 8.8860759 wage: 3.90570784","educ: 9.1139241 wage: 4.02905552","educ: 9.3417722 wage: 4.15240320","educ: 9.5696203 wage: 4.27575088","educ: 9.7974684 wage: 4.39909855","educ: 10.0253165 wage: 4.52244623","educ: 10.2531646 wage: 4.64579391","educ: 10.4810127 wage: 4.76914159","educ: 10.7088608 wage: 4.89248927","educ: 10.9367089 wage: 5.01583695","educ: 11.1645570 wage: 5.13918462","educ: 11.3924051 wage: 5.26253230","educ: 11.6202532 wage: 5.38587998","educ: 11.8481013 wage: 5.50922766","educ: 12.0759494 wage: 5.63257534","educ: 12.3037975 wage: 5.75592302","educ: 12.5316456 wage: 5.87927069","educ: 12.7594937 wage: 6.00261837","educ: 12.9873418 wage: 6.12596605","educ: 13.2151899 wage: 6.24931373","educ: 13.4430380 wage: 6.37266141","educ: 13.6708861 wage: 6.49600908","educ: 13.8987342 wage: 6.61935676","educ: 14.1265823 wage: 6.74270444","educ: 14.3544304 wage: 6.86605212","educ: 14.5822785 wage: 6.98939980","educ: 14.8101266 wage: 7.11274748","educ: 15.0379747 wage: 7.23609515","educ: 15.2658228 wage: 7.35944283","educ: 15.4936709 wage: 7.48279051","educ: 15.7215190 wage: 7.60613819","educ: 15.9493671 wage: 7.72948587","educ: 16.1772152 wage: 7.85283355","educ: 16.4050633 wage: 7.97618122","educ: 16.6329114 wage: 8.09952890","educ: 16.8607595 wage: 8.22287658","educ: 17.0886076 wage: 8.34622426","educ: 17.3164557 wage: 8.46957194","educ: 17.5443038 wage: 8.59291962","educ: 17.7721519 wage: 8.71626729","educ: 18.0000000 wage: 8.83961497"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(51,102,102,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":33.8729763387298},"plot_bgcolor":"transparent","paper_bgcolor":"rgba(213,228,235,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.9,18.9],"tickmode":"array","ticktext":["0","5","10","15"],"tickvals":[0,5,10,15],"categoryorder":"array","categoryarray":["0","5","10","15"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":" Years of Education <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-2.19909416966694,26.274242099946],"tickmode":"array","ticktext":["0","5","10","15","20","25"],"tickvals":[0,5,10,15,20,25],"categoryorder":"array","categoryarray":["0","5","10","15","20","25"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":" Hourly Wages <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"transparent","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":560,"height":430,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"794464a053a9":{"x":{},"y":{},"type":"scatter"},"794426e77385":{"x":{},"y":{}}},"cur_data":"794464a053a9","visdat":{"794464a053a9":["function (y) ","x"],"794426e77385":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script>

]

---

# Fixing Standard Errors

* Given the problem with the homoskedasticity assumption, one can build the standard errors based on some knowledge about the error variance. Robust standard errors `$RSE (\hat{\beta})$` allow for the possibility that the regression line fits more or less well for different values of `$X_{i}$` - a scenario known as heteroskedasticity

* If the residual turns out to be homoskedastic, the estimates of the robust standard error should be close to `$SE(\hat{\beta})$`. However, if residuals are indeed heteroskedastic, estimates of `$RSE(\hat{\beta})$` provide a much better picture of the sampling variance

]

```r
library(wooldridge)
data("wage1", package = "wooldridge") # load data
library(fixest)
reg1<-feols(wage~educ, data=wage1, se="standard")
reg2<-feols(wage~educ, data=wage1, se="hetero")
etable(reg1, reg2)
```

```
##                               reg1               reg2
## Dependent Var.:               wage               wage
##                                                      
## (Intercept)       -0.9049 (0.6850)   -0.9049 (0.7255)
## educ            0.5414*** (0.0532) 0.5414*** (0.0613)
## _______________ __________________ __________________
## S.E. type                 Standard Heteroskedas.-rob.
## Observations                   526                526
## R2                         0.16476            0.16476
## Adj. R2                    0.16316            0.16316
```

]