class: center, middle, inverse, title-slide # Econ 414 - Urban Economics ## Spatial Equilibrium Across Cities ### Marcelino Guerra ### March 2-4, 2021 --- # Introduction * Before, we studied the AMM model to understand prices and population density levels within cities. The Rosen-Roback model is the core tool for understanding prices and population distribution across metro areas * Remember the equation: - Income + Amenities - Housing costs - Transportation costs * Now, income and amenities (e.g., nice weather, low crime rates) differ across space. To compensate for that added complexity, metropolitan areas are treated as a single homogeneous entity - everyone who lives in the area have the same costs of housing and transportation, as well as amenity levels * Both regional housing prices and incomes are likely to vary with amenities * The goal is to analyze the trade-off between income, amenities and housing costs across cities using the Rosen-Roback model * In this framework, it is also possible to compare quality-of-life across areas --- class: inverse,center, middle # Empirical Regularities Across Cities --- # Happiness in US Metro Areas <iframe src="maps/happiness.html" style="width: 1200px; height: 500px; border: 5px" alt=""> --- # Income and Housing Costs <div id="htmlwidget-0ff5d9d76751e5e5b866" style="width:1100px;height:500px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-0ff5d9d76751e5e5b866">{"x":{"data":[{"x":[37540,36647,33007,33678,24968,36903,38774,49889,31563,33780,37237,35392,35355,32028,44347,42331,36404,57516,38422,35804,30076,40638,29453,37212,40052,41736,41623,38829,34781,31265,39589,35415,35275,39640,36173,36286,36213,29386,31997,39843,39198,27948,26939,36019,40648,33631,36824,35344,35824,36864,33644,39830,34694,41200,34027,40481,31978,32319,39306,40882,34985,35886,32980,37615,33516,36655,35856,31602,33474,32516,16048,39125,32083,35117,45941,35192,32366,41406,37714,34870,32617,36217,38779,38604,35083,34935,33481,28687,44739,47710,37165,39478,32764,33784,37179,41863,48822,47332,31346,42145,17075,33249,33014,41097,36696,36990,34395,43861,32123,50770,34410,41270,41073,34015,38282,35912,36881,36768,39071,44655,37968,33253,38610,30950,44947,34185,36684,36035,52929,48376,33018,43035,52380,25296,31917,33816,32192,35384,40987,41580,37968,32392,36294,37386,33107,35013,36534,35324,39282,32426,34294,32355,38638,40248,35281,46823,30790,40860,33174,33031,29665,39573,34394,40235,40110,41762,35936,41158,43721,40827,34264,43531,57265,35512,32119,33638,41585,35737,33487,40084,33038,36256,40246,38115,36717,33190,38342,41453,35438,40131,35486,33256,41918,31474,33981,35923,37838,38360,32885,36729,31462,46039,44472,41132,31798,37882,38338,38361,40694,38567,37159,28667,37043,29674,32517,35100,31855,36535,47278,36393,35636,42043,33071,32386,37295,35416,33774,31363,34062,39457,41291,31195,31287,31404,36344,33993,39267,36561,36358,30997,40003,35193,35653,37684,27145,34320,41674,40046,34462,35598,35704,33493,40333,35547,33242,41427,35016,50814,33151,31454,32587,33128,18194,43074,28318,29984,38162,31589,36068,30746,16322,25670,32946,34252,40275,49342,42023,47670,31705,35099,35970,32807,41735,35990,36174,31585,38704,34130,32965,29877,44039,31915,40087,31956,47534,37297,48009,33999,34278,45278,33892,40245,36287,28959,40032,40711,40745,37176,44021,41974,41777,35363,32423,32424,35194,39638,46260,41143,42148,32166,39482,32015,41387,38137,31949,16743,30501,43640,39824,34246,28959,40753,43914,34146,40310,34258,37970,42022,36251,37620,45214,40108,36298,31282,32021,42519,32882,36153,40119,33926,35957,42233,55525,16568,60983,20044,39458,31913,33893,41340,33305,31806,41730,41844,36281,37204,41245,36871,36173,50957,30186,24468,40266,35035,32444,30634,37064,39641,35921,32802,41683,41485,33665,33574,39859,36399,37171,30817,36779,41210],"y":[971,1070,714,722,861,733,786,1233,776,885,831,820,901,772,1498,1703,743,1653,754,880,1028,1154,904,780,869,929,1055,922,909,647,1086,801,699,804,792,827,814,799,944,978,850,818,744,1088,897,825,844,734,751,840,687,819,711,807,782,888,725,752,1405,1107,763,870,824,1059,998,803,641,697,620,893,425,813,740,928,983,873,792,1031,826,766,820,817,1463,821,907,814,790,986,996,1154,920,857,664,711,838,885,1276,1083,680,787,428,874,844,1106,1094,831,840,1217,956,1259,778,1268,904,738,1015,1130,860,762,860,843,857,655,827,656,820,882,758,914,1404,1411,743,1176,1470,710,864,767,706,895,867,731,868,839,883,861,784,784,970,979,733,638,868,639,796,1003,752,1011,803,937,667,972,854,851,726,1114,986,1152,802,929,1092,786,798,1180,1362,727,1093,1016,817,902,757,800,961,917,1118,849,920,866,898,925,983,1019,1077,672,1085,706,684,958,746,790,629,676,1029,1292,880,919,713,1070,763,758,1002,1087,805,818,805,812,830,737,954,754,1296,792,777,806,811,920,803,1131,755,723,670,738,1228,675,967,669,953,931,910,739,868,750,799,725,934,860,860,737,1014,760,809,778,822,862,937,808,971,933,868,1090,806,682,1125,1036,391,950,815,750,843,954,907,973,417,716,1295,738,746,1233,885,1052,816,846,1099,745,813,876,802,700,1058,714,747,913,1621,1228,1008,854,1133,969,1391,724,1152,1099,1161,744,718,859,1112,1013,933,858,1192,900,1705,1018,1012,698,992,758,1114,1014,1193,1126,1077,704,807,836,682,400,927,945,991,803,976,855,1066,830,918,1000,999,1083,1266,836,876,879,782,728,730,1219,760,1012,1062,861,987,1569,1790,435,2108,512,790,1000,742,882,939,1401,1385,1647,1016,1576,1549,1045,774,1403,957,776,706,857,814,810,746,792,763,763,797,928,745,731,966,864,1159,776,867,834],"text":["incomeE: 37540<br />rentE: 971<br />NAME: Tallahassee, FL Metro Area<br />popE: 380101","incomeE: 36647<br />rentE: 1070<br />NAME: Tampa-St. Petersburg-Clearwater, FL Metro Area<br />popE: 3030047","incomeE: 33007<br />rentE: 714<br />NAME: Terre Haute, IN Metro Area<br />popE: 170313","incomeE: 33678<br />rentE: 722<br />NAME: Texarkana, TX-AR Metro Area<br />popE: 150034","incomeE: 24968<br />rentE: 861<br />NAME: The Villages, FL Metro Area<br />popE: 120999","incomeE: 36903<br />rentE: 733<br />NAME: Toledo, OH Metro Area<br />popE: 604620","incomeE: 38774<br />rentE: 786<br />NAME: Topeka, KS Metro Area<br />popE: 233260","incomeE: 49889<br />rentE: 1233<br />NAME: Trenton, NJ Metro Area<br />popE: 368762","incomeE: 31563<br />rentE: 776<br />NAME: Twin Falls, ID Metro Area<br />popE: 107097","incomeE: 33780<br />rentE: 885<br />NAME: Tucson, AZ Metro Area<br />popE: 1019722","incomeE: 37237<br />rentE: 831<br />NAME: Tulsa, OK Metro Area<br />popE: 985233","incomeE: 35392<br />rentE: 820<br />NAME: Tuscaloosa, AL Metro Area<br />popE: 241398","incomeE: 35355<br />rentE: 901<br />NAME: Tyler, TX Metro Area<br />popE: 225015","incomeE: 32028<br />rentE: 772<br />NAME: Valdosta, GA Metro Area<br />popE: 144564","incomeE: 44347<br />rentE: 1498<br />NAME: Vallejo-Fairfield, CA Metro Area<br />popE: 438530","incomeE: 42331<br />rentE: 1703<br />NAME: Urban Honolulu, HI Metro Area<br />popE: 987638","incomeE: 36404<br />rentE: 743<br />NAME: Utica-Rome, NY Metro Area<br />popE: 293287","incomeE: 57516<br />rentE: 1653<br />NAME: Washington-Arlington-Alexandria, DC-VA-MD-WV Metro Area<br />popE: 6138382","incomeE: 38422<br />rentE: 754<br />NAME: Waterloo-Cedar Falls, IA Metro Area<br />popE: 170132","incomeE: 35804<br />rentE: 880<br />NAME: Victoria, TX Metro Area<br />popE: 99501","incomeE: 30076<br />rentE: 1028<br />NAME: Vineland-Bridgeton, NJ Metro Area<br />popE: 153400","incomeE: 40638<br />rentE: 1154<br />NAME: Virginia Beach-Norfolk-Newport News, VA-NC Metro Area<br />popE: 1722001","incomeE: 29453<br />rentE: 904<br />NAME: Visalia-Porterville, CA Metro Area<br />popE: 460477","incomeE: 37212<br />rentE: 780<br />NAME: Kalamazoo-Portage, MI Metro Area<br />popE: 336845","incomeE: 40052<br />rentE: 869<br />NAME: Kankakee, IL Metro Area<br />popE: 111061","incomeE: 41736<br />rentE: 929<br />NAME: Kansas City, MO-KS Metro Area<br />popE: 2106632","incomeE: 41623<br />rentE: 1055<br />NAME: Houston-The Woodlands-Sugar Land, TX Metro Area<br />popE: 6779104","incomeE: 38829<br />rentE: 922<br />NAME: Kennewick-Richland, WA Metro Area<br />popE: 284828","incomeE: 34781<br />rentE: 909<br />NAME: Killeen-Temple, TX Metro Area<br />popE: 438265","incomeE: 31265<br />rentE: 647<br />NAME: Kingsport-Bristol-Bristol, TN-VA Metro Area<br />popE: 306394","incomeE: 39589<br />rentE: 1086<br />NAME: Kingston, NY Metro Area<br />popE: 179303","incomeE: 35415<br />rentE: 801<br />NAME: Knoxville, TN Metro Area<br />popE: 868499","incomeE: 35275<br />rentE: 699<br />NAME: Kokomo, IN Metro Area<br />popE: 82387","incomeE: 39640<br />rentE: 804<br />NAME: La Crosse-Onalaska, WI-MN Metro Area<br />popE: 136513","incomeE: 36173<br />rentE: 792<br />NAME: Lafayette, LA Metro Area<br />popE: 488969","incomeE: 36286<br />rentE: 827<br />NAME: Lafayette-West Lafayette, IN Metro Area<br />popE: 217955","incomeE: 36213<br />rentE: 814<br />NAME: Lake Charles, LA Metro Area<br />popE: 207050","incomeE: 29386<br />rentE: 799<br />NAME: Lake Havasu City-Kingman, AZ Metro Area<br />popE: 206064","incomeE: 31997<br />rentE: 944<br />NAME: Lakeland-Winter Haven, FL Metro Area<br />popE: 668671","incomeE: 39843<br />rentE: 978<br />NAME: Lancaster, PA Metro Area<br />popE: 538347","incomeE: 39198<br />rentE: 850<br />NAME: Lansing-East Lansing, MI Metro Area<br />popE: 476615","incomeE: 27948<br />rentE: 818<br />NAME: Laredo, TX Metro Area<br />popE: 272053","incomeE: 26939<br />rentE: 744<br />NAME: Las Cruces, NM Metro Area<br />popE: 215338","incomeE: 36019<br />rentE: 1088<br />NAME: Las Vegas-Henderson-Paradise, NV Metro Area<br />popE: 2141574","incomeE: 40648<br />rentE: 897<br />NAME: Lawrence, KS Metro Area<br />popE: 119319","incomeE: 33631<br />rentE: 825<br />NAME: Lawton, OK Metro Area<br />popE: 128490","incomeE: 36824<br />rentE: 844<br />NAME: Lebanon, PA Metro Area<br />popE: 138674","incomeE: 35344<br />rentE: 734<br />NAME: Lewiston, ID-WA Metro Area<br />popE: 62492","incomeE: 35824<br />rentE: 751<br />NAME: Lewiston-Auburn, ME Metro Area<br />popE: 107444","incomeE: 36864<br />rentE: 840<br />NAME: Lexington-Fayette, KY Metro Area<br />popE: 506786","incomeE: 33644<br />rentE: 687<br />NAME: Lima, OH Metro Area<br />popE: 103642","incomeE: 39830<br />rentE: 819<br />NAME: Lincoln, NE Metro Area<br />popE: 327221","incomeE: 34694<br />rentE: 711<br />NAME: Huntington-Ashland, WV-KY-OH Metro Area<br />popE: 358234","incomeE: 41200<br />rentE: 807<br />NAME: Huntsville, AL Metro Area<br />popE: 450612","incomeE: 34027<br />rentE: 782<br />NAME: Idaho Falls, ID Metro Area<br />popE: 142968","incomeE: 40481<br />rentE: 888<br />NAME: Indianapolis-Carmel-Anderson, IN Metro Area<br />popE: 2007497","incomeE: 31978<br />rentE: 725<br />NAME: Jonesboro, AR Metro Area<br />popE: 129755","incomeE: 32319<br />rentE: 752<br />NAME: Joplin, MO Metro Area<br />popE: 177440","incomeE: 39306<br />rentE: 1405<br />NAME: Kahului-Wailuku-Lahaina, HI Metro Area<br />popE: 165356","incomeE: 40882<br />rentE: 1107<br />NAME: Ithaca, NY Metro Area<br />popE: 102962","incomeE: 34985<br />rentE: 763<br />NAME: Jackson, MI Metro Area<br />popE: 158913","incomeE: 35886<br />rentE: 870<br />NAME: Jackson, MS Metro Area<br />popE: 580280","incomeE: 32980<br />rentE: 824<br />NAME: Jackson, TN Metro Area<br />popE: 129331","incomeE: 37615<br />rentE: 1059<br />NAME: Jacksonville, FL Metro Area<br />popE: 1475386","incomeE: 33516<br />rentE: 998<br />NAME: Jacksonville, NC Metro Area<br />popE: 193912","incomeE: 36655<br />rentE: 803<br />NAME: Janesville-Beloit, WI Metro Area<br />popE: 161769","incomeE: 35856<br />rentE: 641<br />NAME: Jefferson City, MO Metro Area<br />popE: 151157","incomeE: 31602<br />rentE: 697<br />NAME: Johnson City, TN Metro Area<br />popE: 201226","incomeE: 33474<br />rentE: 620<br />NAME: Johnstown, PA Metro Area<br />popE: 134550","incomeE: 32516<br />rentE: 893<br />NAME: Abilene, TX Metro Area<br />popE: 170009","incomeE: 16048<br />rentE: 425<br />NAME: Aguadilla-Isabela, PR Metro Area<br />popE: 307555","incomeE: 39125<br />rentE: 813<br />NAME: Akron, OH Metro Area<br />popE: 704454","incomeE: 32083<br />rentE: 740<br />NAME: Albany, GA Metro Area<br />popE: 153101","incomeE: 35117<br />rentE: 928<br />NAME: Albany, OR Metro Area<br />popE: 122870","incomeE: 45941<br />rentE: 983<br />NAME: Albany-Schenectady-Troy, NY Metro Area<br />popE: 880481","incomeE: 35192<br />rentE: 873<br />NAME: Albuquerque, NM Metro Area<br />popE: 910012","incomeE: 32366<br />rentE: 792<br />NAME: Alexandria, LA Metro Area<br />popE: 153894","incomeE: 41406<br />rentE: 1031<br />NAME: Allentown-Bethlehem-Easton, PA-NJ Metro Area<br />popE: 834615","incomeE: 37714<br />rentE: 826<br />NAME: Little Rock-North Little Rock-Conway, AR Metro Area<br />popE: 734502","incomeE: 34870<br />rentE: 766<br />NAME: Logan, UT-ID Metro Area<br />popE: 135615","incomeE: 32617<br />rentE: 820<br />NAME: Longview, TX Metro Area<br />popE: 217858","incomeE: 36217<br />rentE: 817<br />NAME: Longview, WA Metro Area<br />popE: 105112","incomeE: 38779<br />rentE: 1463<br />NAME: Los Angeles-Long Beach-Anaheim, CA Metro Area<br />popE: 13262234","incomeE: 38604<br />rentE: 821<br />NAME: Louisville/Jefferson County, KY-IN Metro Area<br />popE: 1285270","incomeE: 35083<br />rentE: 907<br />NAME: Lubbock, TX Metro Area<br />popE: 313123","incomeE: 34935<br />rentE: 814<br />NAME: Lynchburg, VA Metro Area<br />popE: 260668","incomeE: 33481<br />rentE: 790<br />NAME: Macon-Bibb County, GA Metro Area<br />popE: 229676","incomeE: 28687<br />rentE: 986<br />NAME: Madera, CA Metro Area<br />popE: 155013","incomeE: 44739<br />rentE: 996<br />NAME: Madison, WI Metro Area<br />popE: 647281","incomeE: 47710<br />rentE: 1154<br />NAME: Manchester-Nashua, NH Metro Area<br />popE: 411087","incomeE: 37165<br />rentE: 920<br />NAME: Manhattan, KS Metro Area<br />popE: 98841","incomeE: 39478<br />rentE: 857<br />NAME: Mankato-North Mankato, MN Metro Area<br />popE: 100105","incomeE: 32764<br />rentE: 664<br />NAME: Mansfield, OH Metro Area<br />popE: 121324","incomeE: 33784<br />rentE: 711<br />NAME: Altoona, PA Metro Area<br />popE: 123842","incomeE: 37179<br />rentE: 838<br />NAME: Amarillo, TX Metro Area<br />popE: 263412","incomeE: 41863<br />rentE: 885<br />NAME: Ames, IA Metro Area<br />popE: 96922","incomeE: 48822<br />rentE: 1276<br />NAME: Anchorage, AK Metro Area<br />popE: 399576","incomeE: 47332<br />rentE: 1083<br />NAME: Ann Arbor, MI Metro Area<br />popE: 365961","incomeE: 31346<br />rentE: 680<br />NAME: Anniston-Oxford-Jacksonville, AL Metro Area<br />popE: 115098","incomeE: 42145<br />rentE: 787<br />NAME: Appleton, WI Metro Area<br />popE: 234561","incomeE: 17075<br />rentE: 428<br />NAME: Arecibo, PR Metro Area<br />popE: 183890","incomeE: 33249<br />rentE: 874<br />NAME: Asheville, NC Metro Area<br />popE: 449937","incomeE: 33014<br />rentE: 844<br />NAME: Athens-Clarke County, GA Metro Area<br />popE: 205303","incomeE: 41097<br />rentE: 1106<br />NAME: Atlanta-Sandy Springs-Roswell, GA Metro Area<br />popE: 5779463","incomeE: 36696<br />rentE: 1094<br />NAME: Atlantic City-Hammonton, NJ Metro Area<br />popE: 268539","incomeE: 36990<br />rentE: 831<br />NAME: Auburn-Opelika, AL Metro Area<br />popE: 159287","incomeE: 34395<br />rentE: 840<br />NAME: Augusta-Richmond County, GA-SC Metro Area<br />popE: 594300","incomeE: 43861<br />rentE: 1217<br />NAME: Austin-Round Rock, TX Metro Area<br />popE: 2058351","incomeE: 32123<br />rentE: 956<br />NAME: Bakersfield, CA Metro Area<br />popE: 883053","incomeE: 50770<br />rentE: 1259<br />NAME: Baltimore-Columbia-Towson, MD Metro Area<br />popE: 2793250","incomeE: 34410<br />rentE: 778<br />NAME: Bangor, ME Metro Area<br />popE: 151748","incomeE: 41270<br />rentE: 1268<br />NAME: Barnstable Town, MA Metro Area<br />popE: 213690","incomeE: 41073<br />rentE: 904<br />NAME: Baton Rouge, LA Metro Area<br />popE: 829642","incomeE: 34015<br />rentE: 738<br />NAME: Battle Creek, MI Metro Area<br />popE: 134473","incomeE: 38282<br />rentE: 1015<br />NAME: Bellingham, WA Metro Area<br />popE: 216812","incomeE: 35912<br />rentE: 1130<br />NAME: Bend-Redmond, OR Metro Area<br />popE: 180640","incomeE: 36881<br />rentE: 860<br />NAME: Billings, MT Metro Area<br />popE: 169086","incomeE: 36768<br />rentE: 762<br />NAME: Binghamton, NY Metro Area<br />popE: 243447","incomeE: 39071<br />rentE: 860<br />NAME: Birmingham-Hoover, AL Metro Area<br />popE: 1147054","incomeE: 44655<br />rentE: 843<br />NAME: Bismarck, ND Metro Area<br />popE: 130531","incomeE: 37968<br />rentE: 857<br />NAME: Blacksburg-Christiansburg-Radford, VA Metro Area<br />popE: 182341","incomeE: 33253<br />rentE: 655<br />NAME: Bay City, MI Metro Area<br />popE: 104786","incomeE: 38610<br />rentE: 827<br />NAME: Beaumont-Port Arthur, TX Metro Area<br />popE: 409693","incomeE: 30950<br />rentE: 656<br />NAME: Beckley, WV Metro Area<br />popE: 120358","incomeE: 44947<br />rentE: 820<br />NAME: Bloomington, IL Metro Area<br />popE: 189261","incomeE: 34185<br />rentE: 882<br />NAME: Bloomington, IN Metro Area<br />popE: 166281","incomeE: 36684<br />rentE: 758<br />NAME: Bloomsburg-Berwick, PA Metro Area<br />popE: 84514","incomeE: 36035<br />rentE: 914<br />NAME: Boise City, ID Metro Area<br />popE: 693952","incomeE: 52929<br />rentE: 1404<br />NAME: Boston-Cambridge-Newton, MA-NH Metro Area<br />popE: 4811732","incomeE: 48376<br />rentE: 1411<br />NAME: Boulder, CO Metro Area<br />popE: 321030","incomeE: 33018<br />rentE: 743<br />NAME: Bowling Green, KY Metro Area<br />popE: 172088","incomeE: 43035<br />rentE: 1176<br />NAME: Bremerton-Silverdale, WA Metro Area<br />popE: 262475","incomeE: 52380<br />rentE: 1470<br />NAME: Bridgeport-Stamford-Norwalk, CT Metro Area<br />popE: 944348","incomeE: 25296<br />rentE: 710<br />NAME: Brownsville-Harlingen, TX Metro Area<br />popE: 421750","incomeE: 31917<br />rentE: 864<br />NAME: Brunswick, GA Metro Area<br />popE: 116655","incomeE: 33816<br />rentE: 767<br />NAME: Cape Girardeau, MO-IL Metro Area<br />popE: 97137","incomeE: 32192<br />rentE: 706<br />NAME: Carbondale-Marion, IL Metro Area<br />popE: 125850","incomeE: 35384<br />rentE: 895<br />NAME: Carson City, NV Metro Area<br />popE: 54467","incomeE: 40987<br />rentE: 867<br />NAME: Casper, WY Metro Area<br />popE: 80610","incomeE: 41580<br />rentE: 731<br />NAME: Cedar Rapids, IA Metro Area<br />popE: 268315","incomeE: 37968<br />rentE: 868<br />NAME: Chambersburg-Waynesboro, PA Metro Area<br />popE: 153751","incomeE: 32392<br />rentE: 839<br />NAME: Waco, TX Metro Area<br />popE: 265728","incomeE: 36294<br />rentE: 883<br />NAME: Walla Walla, WA Metro Area<br />popE: 64237","incomeE: 37386<br />rentE: 861<br />NAME: Warner Robins, GA Metro Area<br />popE: 189943","incomeE: 33107<br />rentE: 784<br />NAME: Wichita Falls, TX Metro Area<br />popE: 150994","incomeE: 35013<br />rentE: 784<br />NAME: Williamsport, PA Metro Area<br />popE: 114859","incomeE: 36534<br />rentE: 970<br />NAME: Wilmington, NC Metro Area<br />popE: 283251","incomeE: 35324<br />rentE: 979<br />NAME: Watertown-Fort Drum, NY Metro Area<br />popE: 114448","incomeE: 39282<br />rentE: 733<br />NAME: Wausau, WI Metro Area<br />popE: 135264","incomeE: 32426<br />rentE: 638<br />NAME: Weirton-Steubenville, WV-OH Metro Area<br />popE: 119338","incomeE: 34294<br />rentE: 868<br />NAME: Wenatchee, WA Metro Area<br />popE: 117128","incomeE: 32355<br />rentE: 639<br />NAME: Wheeling, WV-OH Metro Area<br />popE: 142664","incomeE: 38638<br />rentE: 796<br />NAME: Wichita, KS Metro Area<br />popE: 643765","incomeE: 40248<br />rentE: 1003<br />NAME: Winchester, VA-WV Metro Area<br />popE: 136305","incomeE: 35281<br />rentE: 752<br />NAME: Winston-Salem, NC Metro Area<br />popE: 661798","incomeE: 46823<br />rentE: 1011<br />NAME: Worcester, MA-CT Metro Area<br />popE: 938818","incomeE: 30790<br />rentE: 803<br />NAME: Yakima, WA Metro Area<br />popE: 249325","incomeE: 40860<br />rentE: 937<br />NAME: York-Hanover, PA Metro Area<br />popE: 444014","incomeE: 33174<br />rentE: 667<br />NAME: Youngstown-Warren-Boardman, OH-PA Metro Area<br />popE: 545488","incomeE: 33031<br />rentE: 972<br />NAME: Yuba City, CA Metro Area<br />popE: 171365","incomeE: 29665<br />rentE: 854<br />NAME: Yuma, AZ Metro Area<br />popE: 207829","incomeE: 39573<br />rentE: 851<br />NAME: Champaign-Urbana, IL Metro Area<br />popE: 239273","incomeE: 34394<br />rentE: 726<br />NAME: Charleston, WV Metro Area<br />popE: 217312","incomeE: 40235<br />rentE: 1114<br />NAME: Charleston-North Charleston, SC Metro Area<br />popE: 759247","incomeE: 40110<br />rentE: 986<br />NAME: Charlotte-Concord-Gastonia, NC-SC Metro Area<br />popE: 2473125","incomeE: 41762<br />rentE: 1152<br />NAME: Charlottesville, VA Metro Area<br />popE: 230905","incomeE: 35936<br />rentE: 802<br />NAME: Chattanooga, TN-GA Metro Area<br />popE: 552043","incomeE: 41158<br />rentE: 929<br />NAME: Cheyenne, WY Metro Area<br />popE: 97692","incomeE: 43721<br />rentE: 1092<br />NAME: Chicago-Naperville-Elgin, IL-IN-WI Metro Area<br />popE: 9536428","incomeE: 40827<br />rentE: 786<br />NAME: Buffalo-Cheektowaga-Niagara Falls, NY Metro Area<br />popE: 1131570","incomeE: 34264<br />rentE: 798<br />NAME: Burlington, NC Metro Area<br />popE: 160576","incomeE: 43531<br />rentE: 1180<br />NAME: Burlington-South Burlington, VT Metro Area<br />popE: 218042","incomeE: 57265<br />rentE: 1362<br />NAME: California-Lexington Park, MD Metro Area<br />popE: 111531","incomeE: 35512<br />rentE: 727<br />NAME: Canton-Massillon, OH Metro Area<br />popE: 401053","incomeE: 32119<br />rentE: 1093<br />NAME: Cape Coral-Fort Myers, FL Metro Area<br />popE: 718679","incomeE: 33638<br />rentE: 1016<br />NAME: Chico, CA Metro Area<br />popE: 227075","incomeE: 41585<br />rentE: 817<br />NAME: Cincinnati, OH-KY-IN Metro Area<br />popE: 2168825","incomeE: 35737<br />rentE: 902<br />NAME: Clarksville, TN-KY Metro Area<br />popE: 282994","incomeE: 33487<br />rentE: 757<br />NAME: Cleveland, TN Metro Area<br />popE: 121339","incomeE: 40084<br />rentE: 800<br />NAME: Cleveland-Elyria, OH Metro Area<br />popE: 2061766","incomeE: 33038<br />rentE: 961<br />NAME: Coeur d'Alene, ID Metro Area<br />popE: 153605","incomeE: 36256<br />rentE: 917<br />NAME: College Station-Bryan, TX Metro Area<br />popE: 253946","incomeE: 40246<br />rentE: 1118<br />NAME: Colorado Springs, CO Metro Area<br />popE: 712266","incomeE: 38115<br />rentE: 849<br />NAME: Columbia, MO Metro Area<br />popE: 176515","incomeE: 36717<br />rentE: 920<br />NAME: Columbia, SC Metro Area<br />popE: 816664","incomeE: 33190<br />rentE: 866<br />NAME: Columbus, GA-AL Metro Area<br />popE: 307724","incomeE: 38342<br />rentE: 898<br />NAME: Columbus, IN Metro Area<br />popE: 81893","incomeE: 41453<br />rentE: 925<br />NAME: Columbus, OH Metro Area<br />popE: 2054062","incomeE: 35438<br />rentE: 983<br />NAME: Corpus Christi, TX Metro Area<br />popE: 452295","incomeE: 40131<br />rentE: 1019<br />NAME: Corvallis, OR Metro Area<br />popE: 89780","incomeE: 35486<br />rentE: 1077<br />NAME: Crestview-Fort Walton Beach-Destin, FL Metro Area<br />popE: 266595","incomeE: 33256<br />rentE: 672<br />NAME: Cumberland, MD-WV Metro Area<br />popE: 99255","incomeE: 41918<br />rentE: 1085<br />NAME: Dallas-Fort Worth-Arlington, TX Metro Area<br />popE: 7255028","incomeE: 31474<br />rentE: 706<br />NAME: Dalton, GA Metro Area<br />popE: 143406","incomeE: 33981<br />rentE: 684<br />NAME: Danville, IL Metro Area<br />popE: 78407","incomeE: 35923<br />rentE: 958<br />NAME: Daphne-Fairhope-Foley, AL Metro Area<br />popE: 208107","incomeE: 37838<br />rentE: 746<br />NAME: Davenport-Moline-Rock Island, IA-IL Metro Area<br />popE: 382720","incomeE: 38360<br />rentE: 790<br />NAME: Dayton, OH Metro Area<br />popE: 802645","incomeE: 32885<br />rentE: 629<br />NAME: Decatur, AL Metro Area<br />popE: 152293","incomeE: 36729<br />rentE: 676<br />NAME: Decatur, IL Metro Area<br />popE: 106512","incomeE: 31462<br />rentE: 1029<br />NAME: Deltona-Daytona Beach-Ormond Beach, FL Metro Area<br />popE: 634773","incomeE: 46039<br />rentE: 1292<br />NAME: Denver-Aurora-Lakewood, CO Metro Area<br />popE: 2850221","incomeE: 44472<br />rentE: 880<br />NAME: Des Moines-West Des Moines, IA Metro Area<br />popE: 634201","incomeE: 41132<br />rentE: 919<br />NAME: Detroit-Warren-Dearborn, MI Metro Area<br />popE: 4317179","incomeE: 31798<br />rentE: 713<br />NAME: Dothan, AL Metro Area<br />popE: 147967","incomeE: 37882<br />rentE: 1070<br />NAME: Dover, DE Metro Area<br />popE: 174822","incomeE: 38338<br />rentE: 763<br />NAME: Dubuque, IA Metro Area<br />popE: 96802","incomeE: 38361<br />rentE: 758<br />NAME: Duluth, MN-WI Metro Area<br />popE: 279022","incomeE: 40694<br />rentE: 1002<br />NAME: Durham-Chapel Hill, NC Metro Area<br />popE: 558491","incomeE: 38567<br />rentE: 1087<br />NAME: East Stroudsburg, PA Metro Area<br />popE: 167586","incomeE: 37159<br />rentE: 805<br />NAME: Eau Claire, WI Metro Area<br />popE: 166626","incomeE: 28667<br />rentE: 818<br />NAME: El Centro, CA Metro Area<br />popE: 180216","incomeE: 37043<br />rentE: 805<br />NAME: Elmira, NY Metro Area<br />popE: 85740","incomeE: 29674<br />rentE: 812<br />NAME: El Paso, TX Metro Area<br />popE: 841752","incomeE: 32517<br />rentE: 830<br />NAME: Enid, OK Metro Area<br />popE: 62190","incomeE: 35100<br />rentE: 737<br />NAME: Erie, PA Metro Area<br />popE: 275972","incomeE: 31855<br />rentE: 954<br />NAME: Eugene, OR Metro Area<br />popE: 368882","incomeE: 36535<br />rentE: 754<br />NAME: Evansville, IN-KY Metro Area<br />popE: 314967","incomeE: 47278<br />rentE: 1296<br />NAME: Fairbanks, AK Metro Area<br />popE: 99653","incomeE: 36393<br />rentE: 792<br />NAME: Elizabethtown-Fort Knox, KY Metro Area<br />popE: 150577","incomeE: 35636<br />rentE: 777<br />NAME: Elkhart-Goshen, IN Metro Area<br />popE: 203604","incomeE: 42043<br />rentE: 806<br />NAME: Fargo, ND-MN Metro Area<br />popE: 237003","incomeE: 33071<br />rentE: 811<br />NAME: Farmington, NM Metro Area<br />popE: 127455","incomeE: 32386<br />rentE: 920<br />NAME: Fayetteville, NC Metro Area<br />popE: 385345","incomeE: 37295<br />rentE: 803<br />NAME: Fayetteville-Springdale-Rogers, AR-MO Metro Area<br />popE: 526412","incomeE: 35416<br />rentE: 1131<br />NAME: Flagstaff, AZ Metro Area<br />popE: 140217","incomeE: 33774<br />rentE: 755<br />NAME: Flint, MI Metro Area<br />popE: 409361","incomeE: 31363<br />rentE: 723<br />NAME: Florence, SC Metro Area<br />popE: 205814","incomeE: 34062<br />rentE: 670<br />NAME: Florence-Muscle Shoals, AL Metro Area<br />popE: 147080","incomeE: 39457<br />rentE: 738<br />NAME: Fond du Lac, WI Metro Area<br />popE: 102315","incomeE: 41291<br />rentE: 1228<br />NAME: Fort Collins, CO Metro Area<br />popE: 338161","incomeE: 31195<br />rentE: 675<br />NAME: Fort Smith, AR-OK Metro Area<br />popE: 281201","incomeE: 31287<br />rentE: 967<br />NAME: Fresno, CA Metro Area<br />popE: 978130","incomeE: 31404<br />rentE: 669<br />NAME: Gadsden, AL Metro Area<br />popE: 102939","incomeE: 36344<br />rentE: 953<br />NAME: Gainesville, FL Metro Area<br />popE: 280763","incomeE: 33993<br />rentE: 931<br />NAME: Gainesville, GA Metro Area<br />popE: 195961","incomeE: 39267<br />rentE: 910<br />NAME: Gettysburg, PA Metro Area<br />popE: 102023","incomeE: 36561<br />rentE: 739<br />NAME: Fort Wayne, IN Metro Area<br />popE: 431612","incomeE: 36358<br />rentE: 868<br />NAME: Glens Falls, NY Metro Area<br />popE: 126308","incomeE: 30997<br />rentE: 750<br />NAME: Goldsboro, NC Metro Area<br />popE: 124002","incomeE: 40003<br />rentE: 799<br />NAME: Grand Forks, ND-MN Metro Area<br />popE: 101991","incomeE: 35193<br />rentE: 725<br />NAME: Grand Island, NE Metro Area<br />popE: 84729","incomeE: 35653<br />rentE: 934<br />NAME: Grand Junction, CO Metro Area<br />popE: 149998","incomeE: 37684<br />rentE: 860<br />NAME: Grand Rapids-Wyoming, MI Metro Area<br />popE: 1050440","incomeE: 27145<br />rentE: 860<br />NAME: Grants Pass, OR Metro Area<br />popE: 85481","incomeE: 34320<br />rentE: 737<br />NAME: Great Falls, MT Metro Area<br />popE: 81746","incomeE: 41674<br />rentE: 1014<br />NAME: Greeley, CO Metro Area<br />popE: 295123","incomeE: 40046<br />rentE: 760<br />NAME: Green Bay, WI Metro Area<br />popE: 317702","incomeE: 34462<br />rentE: 809<br />NAME: Greensboro-High Point, NC Metro Area<br />popE: 757810","incomeE: 35598<br />rentE: 778<br />NAME: Greenville, NC Metro Area<br />popE: 177372","incomeE: 35704<br />rentE: 822<br />NAME: Greenville-Anderson-Mauldin, SC Metro Area<br />popE: 883853","incomeE: 33493<br />rentE: 862<br />NAME: Gulfport-Biloxi-Pascagoula, MS Metro Area<br />popE: 391293","incomeE: 40333<br />rentE: 937<br />NAME: Hagerstown-Martinsburg, MD-WV Metro Area<br />popE: 263306","incomeE: 35547<br />rentE: 808<br />NAME: Hammond, LA Metro Area<br />popE: 130504","incomeE: 33242<br />rentE: 971<br />NAME: Hanford-Corcoran, CA Metro Area<br />popE: 150075","incomeE: 41427<br />rentE: 933<br />NAME: Harrisburg-Carlisle, PA Metro Area<br />popE: 567872","incomeE: 35016<br />rentE: 868<br />NAME: Harrisonburg, VA Metro Area<br />popE: 132835","incomeE: 50814<br />rentE: 1090<br />NAME: Hartford-West Hartford-East Hartford, CT Metro Area<br />popE: 1209367","incomeE: 33151<br />rentE: 806<br />NAME: Hattiesburg, MS Metro Area<br />popE: 148768","incomeE: 31454<br />rentE: 682<br />NAME: Hickory-Lenoir-Morganton, NC Metro Area<br />popE: 365339","incomeE: 32587<br />rentE: 1125<br />NAME: Hilton Head Island-Bluffton-Beaufort, SC Metro Area<br />popE: 210558","incomeE: 33128<br />rentE: 1036<br />NAME: Hinesville, GA Metro Area<br />popE: 80264","incomeE: 18194<br />rentE: 391<br />NAME: Guayama, PR Metro Area<br />popE: 77151","incomeE: 43074<br />rentE: 950<br />NAME: Iowa City, IA Metro Area<br />popE: 169144","incomeE: 28318<br />rentE: 815<br />NAME: Homosassa Springs, FL Metro Area<br />popE: 143087","incomeE: 29984<br />rentE: 750<br />NAME: Hot Springs, AR Metro Area<br />popE: 98296","incomeE: 38162<br />rentE: 843<br />NAME: Houma-Thibodaux, LA Metro Area<br />popE: 210801","incomeE: 31589<br />rentE: 954<br />NAME: Medford, OR Metro Area<br />popE: 214267","incomeE: 36068<br />rentE: 907<br />NAME: Memphis, TN-MS-AR Metro Area<br />popE: 1345991","incomeE: 30746<br />rentE: 973<br />NAME: Merced, CA Metro Area<br />popE: 269075","incomeE: 16322<br />rentE: 417<br />NAME: Mayagüez, PR Metro Area<br />popE: 93435","incomeE: 25670<br />rentE: 716<br />NAME: McAllen-Edinburg-Mission, TX Metro Area<br />popE: 849389","incomeE: 32946<br />rentE: 1295<br />NAME: Miami-Fort Lauderdale-West Palm Beach, FL Metro Area<br />popE: 6070944","incomeE: 34252<br />rentE: 738<br />NAME: Michigan City-La Porte, IN Metro Area<br />popE: 110552","incomeE: 40275<br />rentE: 746<br />NAME: Midland, MI Metro Area<br />popE: 83389","incomeE: 49342<br />rentE: 1233<br />NAME: Midland, TX Metro Area<br />popE: 169808","incomeE: 42023<br />rentE: 885<br />NAME: Milwaukee-Waukesha-West Allis, WI Metro Area<br />popE: 1575907","incomeE: 47670<br />rentE: 1052<br />NAME: Minneapolis-St. Paul-Bloomington, MN-WI Metro Area<br />popE: 3557528","incomeE: 31705<br />rentE: 816<br />NAME: Missoula, MT Metro Area<br />popE: 115983","incomeE: 35099<br />rentE: 846<br />NAME: Mobile, AL Metro Area<br />popE: 414659","incomeE: 35970<br />rentE: 1099<br />NAME: Modesto, CA Metro Area<br />popE: 539301","incomeE: 32807<br />rentE: 745<br />NAME: Monroe, LA Metro Area<br />popE: 178550","incomeE: 41735<br />rentE: 813<br />NAME: Monroe, MI Metro Area<br />popE: 149699","incomeE: 35990<br />rentE: 876<br />NAME: Montgomery, AL Metro Area<br />popE: 373589","incomeE: 36174<br />rentE: 802<br />NAME: Morgantown, WV Metro Area<br />popE: 139089","incomeE: 31585<br />rentE: 700<br />NAME: Morristown, TN Metro Area<br />popE: 116987","incomeE: 38704<br />rentE: 1058<br />NAME: Mount Vernon-Anacortes, WA Metro Area<br />popE: 123907","incomeE: 34130<br />rentE: 714<br />NAME: Muncie, IN Metro Area<br />popE: 115616","incomeE: 32965<br />rentE: 747<br />NAME: Muskegon, MI Metro Area<br />popE: 173043","incomeE: 29877<br />rentE: 913<br />NAME: Myrtle Beach-Conway-North Myrtle Beach, SC-NC Metro Area<br />popE: 447775","incomeE: 44039<br />rentE: 1621<br />NAME: Napa, CA Metro Area<br />popE: 140530","incomeE: 31915<br />rentE: 1228<br />NAME: Naples-Immokalee-Marco Island, FL Metro Area<br />popE: 363922","incomeE: 40087<br />rentE: 1008<br />NAME: Nashville-Davidson--Murfreesboro--Franklin, TN Metro Area<br />popE: 1864138","incomeE: 31956<br />rentE: 854<br />NAME: New Bern, NC Metro Area<br />popE: 125519","incomeE: 47534<br />rentE: 1133<br />NAME: New Haven-Milford, CT Metro Area<br />popE: 859339","incomeE: 37297<br />rentE: 969<br />NAME: New Orleans-Metairie, LA Metro Area<br />popE: 1263635","incomeE: 48009<br />rentE: 1391<br />NAME: New York-Newark-Jersey City, NY-NJ-PA Metro Area<br />popE: 19990592","incomeE: 33999<br />rentE: 724<br />NAME: Niles-Benton Harbor, MI Metro Area<br />popE: 154807","incomeE: 34278<br />rentE: 1152<br />NAME: North Port-Sarasota-Bradenton, FL Metro Area<br />popE: 785997","incomeE: 45278<br />rentE: 1099<br />NAME: Norwich-New London, CT Metro Area<br />popE: 268881","incomeE: 33892<br />rentE: 1161<br />NAME: Orlando-Kissimmee-Sanford, FL Metro Area<br />popE: 2450261","incomeE: 40245<br />rentE: 744<br />NAME: Oshkosh-Neenah, WI Metro Area<br />popE: 169926","incomeE: 36287<br />rentE: 718<br />NAME: Owensboro, KY Metro Area<br />popE: 117987","incomeE: 28959<br />rentE: 859<br />NAME: Ocala, FL Metro Area<br />popE: 348371","incomeE: 40032<br />rentE: 1112<br />NAME: Ocean City, NJ Metro Area<br />popE: 93705","incomeE: 40711<br />rentE: 1013<br />NAME: Odessa, TX Metro Area<br />popE: 158342","incomeE: 40745<br />rentE: 933<br />NAME: Ogden-Clearfield, UT Metro Area<br />popE: 652744","incomeE: 37176<br />rentE: 858<br />NAME: Oklahoma City, OK Metro Area<br />popE: 1369759","incomeE: 44021<br />rentE: 1192<br />NAME: Olympia-Tumwater, WA Metro Area<br />popE: 274684","incomeE: 41974<br />rentE: 900<br />NAME: Omaha-Council Bluffs, NE-IA Metro Area<br />popE: 922891","incomeE: 41777<br />rentE: 1705<br />NAME: Oxnard-Thousand Oaks-Ventura, CA Metro Area<br />popE: 848112","incomeE: 35363<br />rentE: 1018<br />NAME: Palm Bay-Melbourne-Titusville, FL Metro Area<br />popE: 576808","incomeE: 32423<br />rentE: 1012<br />NAME: Panama City, FL Metro Area<br />popE: 198537","incomeE: 32424<br />rentE: 698<br />NAME: Parkersburg-Vienna, WV Metro Area<br />popE: 91353","incomeE: 35194<br />rentE: 992<br />NAME: Pensacola-Ferry Pass-Brent, FL Metro Area<br />popE: 481964","incomeE: 39638<br />rentE: 758<br />NAME: Peoria, IL Metro Area<br />popE: 374426","incomeE: 46260<br />rentE: 1114<br />NAME: Philadelphia-Camden-Wilmington, PA-NJ-DE-MD Metro Area<br />popE: 6069448","incomeE: 41143<br />rentE: 1014<br />NAME: Portland-South Portland, ME Metro Area<br />popE: 529323","incomeE: 42148<br />rentE: 1193<br />NAME: Portland-Vancouver-Hillsboro, OR-WA Metro Area<br />popE: 2417931","incomeE: 32166<br />rentE: 1126<br />NAME: Port St. Lucie, FL Metro Area<br />popE: 463172","incomeE: 39482<br />rentE: 1077<br />NAME: Phoenix-Mesa-Scottsdale, AZ Metro Area<br />popE: 4673634","incomeE: 32015<br />rentE: 704<br />NAME: Pine Bluff, AR Metro Area<br />popE: 92345","incomeE: 41387<br />rentE: 807<br />NAME: Pittsburgh, PA Metro Area<br />popE: 2339941","incomeE: 38137<br />rentE: 836<br />NAME: Pittsfield, MA Metro Area<br />popE: 127328","incomeE: 31949<br />rentE: 682<br />NAME: Pocatello, ID Metro Area<br />popE: 85065","incomeE: 16743<br />rentE: 400<br />NAME: Ponce, PR Metro Area<br />popE: 307093","incomeE: 30501<br />rentE: 927<br />NAME: Prescott, AZ Metro Area<br />popE: 224645","incomeE: 43640<br />rentE: 945<br />NAME: Providence-Warwick, RI-MA Metro Area<br />popE: 1615516","incomeE: 39824<br />rentE: 991<br />NAME: Provo-Orem, UT Metro Area<br />popE: 601388","incomeE: 34246<br />rentE: 803<br />NAME: Pueblo, CO Metro Area<br />popE: 164685","incomeE: 28959<br />rentE: 976<br />NAME: Punta Gorda, FL Metro Area<br />popE: 176954","incomeE: 40753<br />rentE: 855<br />NAME: Racine, WI Metro Area<br />popE: 195398","incomeE: 43914<br />rentE: 1066<br />NAME: Raleigh, NC Metro Area<br />popE: 1302632","incomeE: 34146<br />rentE: 830<br />NAME: Rapid City, SD Metro Area<br />popE: 145291","incomeE: 40310<br />rentE: 918<br />NAME: Reading, PA Metro Area<br />popE: 416642","incomeE: 34258<br />rentE: 1000<br />NAME: Redding, CA Metro Area<br />popE: 179085","incomeE: 37970<br />rentE: 999<br />NAME: Reno, NV Metro Area<br />popE: 454427","incomeE: 42022<br />rentE: 1083<br />NAME: Richmond, VA Metro Area<br />popE: 1281530","incomeE: 36251<br />rentE: 1266<br />NAME: Riverside-San Bernardino-Ontario, CA Metro Area<br />popE: 4518699","incomeE: 37620<br />rentE: 836<br />NAME: Roanoke, VA Metro Area<br />popE: 313291","incomeE: 45214<br />rentE: 876<br />NAME: Rochester, MN Metro Area<br />popE: 216035","incomeE: 40108<br />rentE: 879<br />NAME: Rochester, NY Metro Area<br />popE: 1074667","incomeE: 36298<br />rentE: 782<br />NAME: Rockford, IL Metro Area<br />popE: 339780","incomeE: 31282<br />rentE: 728<br />NAME: Rocky Mount, NC Metro Area<br />popE: 147335","incomeE: 32021<br />rentE: 730<br />NAME: Rome, GA Metro Area<br />popE: 96824","incomeE: 42519<br />rentE: 1219<br />NAME: Sacramento--Roseville--Arden-Arcade, CA Metro Area<br />popE: 2291738","incomeE: 32882<br />rentE: 760<br />NAME: Saginaw, MI Metro Area<br />popE: 192778","incomeE: 36153<br />rentE: 1012<br />NAME: Salisbury, MD-DE Metro Area<br />popE: 399013","incomeE: 40119<br />rentE: 1062<br />NAME: Salt Lake City, UT Metro Area<br />popE: 1185990","incomeE: 33926<br />rentE: 861<br />NAME: San Angelo, TX Metro Area<br />popE: 118990","incomeE: 35957<br />rentE: 987<br />NAME: San Antonio-New Braunfels, TX Metro Area<br />popE: 2426204","incomeE: 42233<br />rentE: 1569<br />NAME: San Diego-Carlsbad, CA Metro Area<br />popE: 3302833","incomeE: 55525<br />rentE: 1790<br />NAME: San Francisco-Oakland-Hayward, CA Metro Area<br />popE: 4673221","incomeE: 16568<br />rentE: 435<br />NAME: San Germán, PR Metro Area<br />popE: 127488","incomeE: 60983<br />rentE: 2108<br />NAME: San Jose-Sunnyvale-Santa Clara, CA Metro Area<br />popE: 1981616","incomeE: 20044<br />rentE: 512<br />NAME: San Juan-Carolina-Caguas, PR Metro Area<br />popE: 2142392","incomeE: 39458<br />rentE: 790<br />NAME: St. Cloud, MN Metro Area<br />popE: 196598","incomeE: 31913<br />rentE: 1000<br />NAME: St. George, UT Metro Area<br />popE: 160537","incomeE: 33893<br />rentE: 742<br />NAME: St. Joseph, MO-KS Metro Area<br />popE: 126779","incomeE: 41340<br />rentE: 882<br />NAME: St. Louis, MO-IL Metro Area<br />popE: 2805551","incomeE: 33305<br />rentE: 939<br />NAME: Salem, OR Metro Area<br />popE: 416980","incomeE: 31806<br />rentE: 1401<br />NAME: Salinas, CA Metro Area<br />popE: 433212","incomeE: 41730<br />rentE: 1385<br />NAME: San Luis Obispo-Paso Robles-Arroyo Grande, CA Metro Area<br />popE: 281455","incomeE: 41844<br />rentE: 1647<br />NAME: Santa Cruz-Watsonville, CA Metro Area<br />popE: 273765","incomeE: 36281<br />rentE: 1016<br />NAME: Santa Fe, NM Metro Area<br />popE: 148917","incomeE: 37204<br />rentE: 1576<br />NAME: Santa Maria-Santa Barbara, CA Metro Area<br />popE: 443738","incomeE: 41245<br />rentE: 1549<br />NAME: Santa Rosa, CA Metro Area<br />popE: 501317","incomeE: 36871<br />rentE: 1045<br />NAME: Savannah, GA Metro Area<br />popE: 381623","incomeE: 36173<br />rentE: 774<br />NAME: Scranton--Wilkes-Barre--Hazleton, PA Metro Area<br />popE: 556926","incomeE: 50957<br />rentE: 1403<br />NAME: Seattle-Tacoma-Bellevue, WA Metro Area<br />popE: 3809717","incomeE: 30186<br />rentE: 957<br />NAME: Sebastian-Vero Beach, FL Metro Area<br />popE: 150984","incomeE: 24468<br />rentE: 776<br />NAME: Sebring, FL Metro Area<br />popE: 102101","incomeE: 40266<br />rentE: 706<br />NAME: Sheboygan, WI Metro Area<br />popE: 115205","incomeE: 35035<br />rentE: 857<br />NAME: Sherman-Denison, TX Metro Area<br />popE: 128560","incomeE: 32444<br />rentE: 814<br />NAME: Shreveport-Bossier City, LA Metro Area<br />popE: 441339","incomeE: 30634<br />rentE: 810<br />NAME: Sierra Vista-Douglas, AZ Metro Area<br />popE: 126279","incomeE: 37064<br />rentE: 746<br />NAME: Sioux City, IA-NE-SD Metro Area<br />popE: 168677","incomeE: 39641<br />rentE: 792<br />NAME: Sioux Falls, SD Metro Area<br />popE: 255438","incomeE: 35921<br />rentE: 763<br />NAME: South Bend-Mishawaka, IN-MI Metro Area<br />popE: 320700","incomeE: 32802<br />rentE: 763<br />NAME: Spartanburg, SC Metro Area<br />popE: 329839","incomeE: 41683<br />rentE: 797<br />NAME: Springfield, IL Metro Area<br />popE: 210028","incomeE: 41485<br />rentE: 928<br />NAME: Springfield, MA Metro Area<br />popE: 630275","incomeE: 33665<br />rentE: 745<br />NAME: Springfield, MO Metro Area<br />popE: 458834","incomeE: 33574<br />rentE: 731<br />NAME: Springfield, OH Metro Area<br />popE: 135198","incomeE: 39859<br />rentE: 966<br />NAME: State College, PA Metro Area<br />popE: 161443","incomeE: 36399<br />rentE: 864<br />NAME: Staunton-Waynesboro, VA Metro Area<br />popE: 121079","incomeE: 37171<br />rentE: 1159<br />NAME: Stockton-Lodi, CA Metro Area<br />popE: 732212","incomeE: 30817<br />rentE: 776<br />NAME: Sumter, SC Metro Area<br />popE: 106995","incomeE: 36779<br />rentE: 867<br />NAME: Spokane-Spokane Valley, WA Metro Area<br />popE: 555308","incomeE: 41210<br />rentE: 834<br />NAME: Syracuse, NY Metro Area<br />popE: 654705"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,139,1)","opacity":1,"size":[6.19472154591903,11.0803697676654,5.22007534117096,5.08792932993688,4.87122536170719,6.91879914729421,5.56915406127713,6.15229887045033,4.75049313231205,7.9377543932641,7.86279101596631,5.60942947297249,5.52740292732801,5.04993290289232,6.40246771334969,7.86806297109666,5.84787023946798,14.2190039301009,5.21894953158686,4.67769520863731,5.11077178178823,9.2449595632108,6.47636961340089,6.02859550357524,4.78639510354982,9.84260736793679,14.7549582019128,5.81090967340554,6.40156265469805,5.90386989512052,5.2749265009348,7.59816024411576,4.48673179566777,4.99184360405386,6.56939158354879,5.49084307211898,5.43278399290778,5.42743361686887,7.09651224900508,6.72365078051861,6.52944410912105,5.75377971494594,5.47709105421504,9.89400721112366,4.8573540009264,4.9310449141847,5.00770536290687,4.15867634289735,4.75368875765698,6.62601690238225,4.71808170188853,5.98993691892445,6.11221978924706,6.44340497607297,5.03863049241982,9.69434852951464,4.94084253593872,5.26372620405263,5.18891819029731,4.71156987121334,5.14736048252961,6.84856937917267,4.93756782569959,8.82465112491109,5.36000616006889,5.16593555727287,5.09559433907197,5.40092513230622,4.97725310807908,5.21818397590096,5.908759260766,7.19176687071826,5.10875858486058,4.8864691906902,7.62616142500677,7.69431850756101,5.11409127958494,7.51784043402159,7.26974737163602,4.98519090258262,5.49033532159808,4.73200661439356,19.161139348993,8.47502296329467,5.93205365508483,5.70143527476719,5.55112625607504,5.1215801834284,7.03824250491743,6.3070207517537,4.67108932601371,4.68369829925065,4.87388851290513,4.89430621470695,5.71418081354985,4.65159800629889,6.26589488163596,6.14170212790828,4.82168782831882,5.57565343178399,5.30215228479286,6.44113448941729,5.42329226091036,13.906386030941,5.7377728011269,5.14980726064814,6.8892158721406,9.77086024318223,7.63214549596026,10.7838472268282,5.09961032082947,5.46837355276138,7.50590657602001,4.97667716158265,5.48485038623852,5.282913073641,5.2124261456769,5.61943115867747,8.20352799559226,4.94681208072938,5.29301308497008,4.72893612896385,6.30207602717536,4.86595367321953,5.33342527140825,5.19478432166555,4.51317550379891,7.16408841817359,13.0108903461751,5.96470687236861,5.23106947180197,5.70983802721616,7.77210284200637,6.34452868629642,4.83498430903344,4.65380338102234,4.91032429116479,3.77952755905512,4.46385642289813,5.73674800166269,5.11313122205102,5.72487336204023,4.19787241059118,5.33735134059303,5.09448455848239,4.81963176585551,5.80394453817206,4.81608648976747,4.98258057057627,4.85751187734255,4.83899059120864,5.03646612954313,7.02856435862377,4.99030591935227,7.07790135421977,7.7596779505439,5.64782606751826,6.42112769814756,6.74529559345366,5.2266013814637,5.43699890264444,5.59899873676222,5.48747444581236,7.33268075247565,10.3617776368906,5.55732881982392,6.76502607058055,4.65947077568062,16.8122824981019,8.17206795832512,5.15820686726092,5.49129834910482,4.79056735938125,6.27120978746015,7.22890330640831,5.53792728325536,9.93379561351733,5.80280717420437,4.87401127113293,9.77596325598913,5.11215030988124,5.66984933778685,7.21221096987531,5.25813361380099,7.47458134346018,5.9094700414167,4.48044744655209,9.7644450538237,6.44905764619679,4.5748705423084,5.72886105479074,4.67523871127166,15.1367024521803,5.04174235797714,4.43438869902143,5.43850047542453,6.20441452257101,7.44044229064643,5.10330292409299,4.74508174989949,7.0036808146624,10.8563227061754,7.00209142015234,12.5178917817337,5.07370239819824,5.24784249101381,4.65036467093019,5.78514691162497,6.78430807906715,5.20301921351952,5.19696601416826,5.28038491040549,4.5279932874601,7.53490104099471,4.15147379166701,5.77147976397114,6.15275179745258,5.939712879803,4.67920969190515,5.09164115425242,5.41400845214322,5.58778979052617,4.92296623664466,6.21409098130394,6.68711538239882,5.01890678135599,6.30089694419024,5.42607426772869,5.06754909029721,4.70533153474296,6.03383021198146,5.79485431934636,7.84718077328076,4.7113488224914,5.79290679529846,5.37157556386128,4.70250227892884,6.37873728822299,4.91394613968703,4.895590984887,4.70219169602449,4.51579561808478,5.08768286985938,8.00340131423811,4.52488748274705,4.47856650039237,5.85580551817669,5.95102320679951,7.32905658150423,5.26331579093822,7.63400489906851,6.2358758741367,5.71369001630529,4.94660489020952,5.08820996404815,6.81214196505884,4.96435888614406,8.32793474941564,5.07923407378482,6.13934252100368,5.45168081265992,4.45931282715348,4.4169787928634,5.21278864058177,5.0394767140207,4.66559734476896,5.4529818973487,5.47143084632705,8.5894534743078,5.74022282554322,4.6150174606452,7.55307144373978,14.1609837867866,4.78185705072467,4.49931009907475,5.21693206832075,9.0000571500247,11.7010926786019,4.82926621684924,6.31964723229035,6.72655161392471,5.27040962046373,5.08563408479832,6.17045017079045,5.01072807685188,4.83779791619167,4.89482833108754,4.82613020014357,5.2369503098472,6.43384913218695,5.02116667841047,6.13395818764734,9.47312765556047,4.90769951619504,7.57661463321517,8.43357139328723,22.6771653543307,5.12020467077217,7.39948293864357,5.73933641664234,10.3305921769151,5.217667151133,4.84622779573638,6.07403724395512,4.61790691955807,5.14361642822521,7.05322320191195,8.63351039220574,5.76567995140546,7.72367421803799,7.55003922649732,6.83841998982571,5.38600238664156,4.59239162960535,6.54681124273118,6.1735835989857,14.1596930294162,6.69606873139878,10.2862404295918,6.48530531497678,12.8759156027631,4.60324956153186,10.1779850538735,4.9219710049848,4.51987173945434,5.90681496790542,5.52550590999267,9.06757587356823,6.90956437883767,5.18464754086167,5.26079045948416,5.36840505339801,8.50802487540744,5.05504810675135,6.32662981877225,5.27362022944606,6.45620122742211,8.46788351297585,12.7220600108113,5.93275258664531,5.48076456566546,8.05446541989057,6.04025354786812,5.06932108621729,4.65059091314254,10.1101504438286,5.35356662691128,6.26386596298078,8.28166594145334,4.85461656970318,10.2976184348361,11.407684591858,12.8755089393712,4.92322469839333,9.65502706030505,9.89520531797148,5.3751552059075,5.15795347954388,4.91765877074196,10.7995592433957,6.32781808382895,6.38424489689199,5.79598284377285,5.76153135633568,5.08026046711348,6.42019172530535,6.60875608261497,6.20035922499383,6.7796395141714,11.9812784437449,5.09441644328882,4.70325888726968,4.82260701152697,4.9315892528869,6.41204220505873,4.91371715164747,5.20986732354139,5.67690548408515,5.9633538479587,6.00051977349387,5.44883953801109,6.99116116743833,6.47090742869016,4.98208910603919,5.16382789470482,4.8718815090213,7.26386580418392,4.7495517821257,6.77480519409565,7.05858398396521],"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,139,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[16048,16616.7974683544,17185.5949367089,17754.3924050633,18323.1898734177,18891.9873417722,19460.7848101266,20029.582278481,20598.3797468354,21167.1772151899,21735.9746835443,22304.7721518987,22873.5696202532,23442.3670886076,24011.164556962,24579.9620253165,25148.7594936709,25717.5569620253,26286.3544303797,26855.1518987342,27423.9493670886,27992.746835443,28561.5443037975,29130.3417721519,29699.1392405063,30267.9367088608,30836.7341772152,31405.5316455696,31974.3291139241,32543.1265822785,33111.9240506329,33680.7215189873,34249.5189873418,34818.3164556962,35387.1139240506,35955.9113924051,36524.7088607595,37093.5063291139,37662.3037974684,38231.1012658228,38799.8987341772,39368.6962025316,39937.4936708861,40506.2911392405,41075.0886075949,41643.8860759494,42212.6835443038,42781.4810126582,43350.2784810127,43919.0759493671,44487.8734177215,45056.670886076,45625.4683544304,46194.2658227848,46763.0632911392,47331.8607594937,47900.6582278481,48469.4556962025,49038.253164557,49607.0506329114,50175.8481012658,50744.6455696203,51313.4430379747,51882.2405063291,52451.0379746835,53019.835443038,53588.6329113924,54157.4303797468,54726.2278481013,55295.0253164557,55863.8227848101,56432.6202531646,57001.417721519,57570.2151898734,58139.0126582279,58707.8101265823,59276.6075949367,59845.4050632911,60414.2025316456,60983],"y":[412.866807569779,426.549546241568,440.232284913358,453.915023585147,467.597762256937,481.280500928727,494.963239600516,508.645978272306,522.328716944095,536.011455615885,549.694194287674,563.376932959464,577.059671631253,590.742410303043,604.425148974832,618.107887646622,631.790626318411,645.473364990201,659.156103661991,672.83884233378,686.52158100557,700.204319677359,713.887058349149,727.569797020938,741.252535692728,754.935274364518,768.618013036307,782.300751708097,795.983490379886,809.666229051676,823.348967723465,837.031706395255,850.714445067044,864.397183738834,878.079922410623,891.762661082413,905.445399754203,919.128138425992,932.810877097782,946.493615769571,960.176354441361,973.85909311315,987.54183178494,1001.22457045673,1014.90730912852,1028.59004780031,1042.2727864721,1055.95552514389,1069.63826381568,1083.32100248747,1097.00374115926,1110.68647983105,1124.36921850284,1138.05195717463,1151.73469584641,1165.4174345182,1179.10017318999,1192.78291186178,1206.46565053357,1220.14838920536,1233.83112787715,1247.51386654894,1261.19660522073,1274.87934389252,1288.56208256431,1302.2448212361,1315.92755990789,1329.61029857968,1343.29303725147,1356.97577592326,1370.65851459505,1384.34125326684,1398.02399193863,1411.70673061042,1425.38946928221,1439.072207954,1452.75494662578,1466.43768529757,1480.12042396936,1493.80316264115],"text":["incomeE: 16048.00<br />rentE: 412.8668<br />popE: 1","incomeE: 16616.80<br />rentE: 426.5495<br />popE: 1","incomeE: 17185.59<br />rentE: 440.2323<br />popE: 1","incomeE: 17754.39<br />rentE: 453.9150<br />popE: 1","incomeE: 18323.19<br />rentE: 467.5978<br />popE: 1","incomeE: 18891.99<br />rentE: 481.2805<br />popE: 1","incomeE: 19460.78<br />rentE: 494.9632<br />popE: 1","incomeE: 20029.58<br />rentE: 508.6460<br />popE: 1","incomeE: 20598.38<br />rentE: 522.3287<br />popE: 1","incomeE: 21167.18<br />rentE: 536.0115<br />popE: 1","incomeE: 21735.97<br />rentE: 549.6942<br />popE: 1","incomeE: 22304.77<br />rentE: 563.3769<br />popE: 1","incomeE: 22873.57<br />rentE: 577.0597<br />popE: 1","incomeE: 23442.37<br />rentE: 590.7424<br />popE: 1","incomeE: 24011.16<br />rentE: 604.4251<br />popE: 1","incomeE: 24579.96<br />rentE: 618.1079<br />popE: 1","incomeE: 25148.76<br />rentE: 631.7906<br />popE: 1","incomeE: 25717.56<br />rentE: 645.4734<br />popE: 1","incomeE: 26286.35<br />rentE: 659.1561<br />popE: 1","incomeE: 26855.15<br />rentE: 672.8388<br />popE: 1","incomeE: 27423.95<br />rentE: 686.5216<br />popE: 1","incomeE: 27992.75<br />rentE: 700.2043<br />popE: 1","incomeE: 28561.54<br />rentE: 713.8871<br />popE: 1","incomeE: 29130.34<br />rentE: 727.5698<br />popE: 1","incomeE: 29699.14<br />rentE: 741.2525<br />popE: 1","incomeE: 30267.94<br />rentE: 754.9353<br />popE: 1","incomeE: 30836.73<br />rentE: 768.6180<br />popE: 1","incomeE: 31405.53<br />rentE: 782.3008<br />popE: 1","incomeE: 31974.33<br />rentE: 795.9835<br />popE: 1","incomeE: 32543.13<br />rentE: 809.6662<br />popE: 1","incomeE: 33111.92<br />rentE: 823.3490<br />popE: 1","incomeE: 33680.72<br />rentE: 837.0317<br />popE: 1","incomeE: 34249.52<br />rentE: 850.7144<br />popE: 1","incomeE: 34818.32<br />rentE: 864.3972<br />popE: 1","incomeE: 35387.11<br />rentE: 878.0799<br />popE: 1","incomeE: 35955.91<br />rentE: 891.7627<br />popE: 1","incomeE: 36524.71<br />rentE: 905.4454<br />popE: 1","incomeE: 37093.51<br />rentE: 919.1281<br />popE: 1","incomeE: 37662.30<br />rentE: 932.8109<br />popE: 1","incomeE: 38231.10<br />rentE: 946.4936<br />popE: 1","incomeE: 38799.90<br />rentE: 960.1764<br />popE: 1","incomeE: 39368.70<br />rentE: 973.8591<br />popE: 1","incomeE: 39937.49<br />rentE: 987.5418<br />popE: 1","incomeE: 40506.29<br />rentE: 1001.2246<br />popE: 1","incomeE: 41075.09<br />rentE: 1014.9073<br />popE: 1","incomeE: 41643.89<br />rentE: 1028.5900<br />popE: 1","incomeE: 42212.68<br />rentE: 1042.2728<br />popE: 1","incomeE: 42781.48<br />rentE: 1055.9555<br />popE: 1","incomeE: 43350.28<br />rentE: 1069.6383<br />popE: 1","incomeE: 43919.08<br />rentE: 1083.3210<br />popE: 1","incomeE: 44487.87<br />rentE: 1097.0037<br />popE: 1","incomeE: 45056.67<br />rentE: 1110.6865<br />popE: 1","incomeE: 45625.47<br />rentE: 1124.3692<br />popE: 1","incomeE: 46194.27<br />rentE: 1138.0520<br />popE: 1","incomeE: 46763.06<br />rentE: 1151.7347<br />popE: 1","incomeE: 47331.86<br />rentE: 1165.4174<br />popE: 1","incomeE: 47900.66<br />rentE: 1179.1002<br />popE: 1","incomeE: 48469.46<br />rentE: 1192.7829<br />popE: 1","incomeE: 49038.25<br />rentE: 1206.4657<br />popE: 1","incomeE: 49607.05<br />rentE: 1220.1484<br />popE: 1","incomeE: 50175.85<br />rentE: 1233.8311<br />popE: 1","incomeE: 50744.65<br />rentE: 1247.5139<br />popE: 1","incomeE: 51313.44<br />rentE: 1261.1966<br />popE: 1","incomeE: 51882.24<br />rentE: 1274.8793<br />popE: 1","incomeE: 52451.04<br />rentE: 1288.5621<br />popE: 1","incomeE: 53019.84<br />rentE: 1302.2448<br />popE: 1","incomeE: 53588.63<br />rentE: 1315.9276<br />popE: 1","incomeE: 54157.43<br />rentE: 1329.6103<br />popE: 1","incomeE: 54726.23<br />rentE: 1343.2930<br />popE: 1","incomeE: 55295.03<br />rentE: 1356.9758<br />popE: 1","incomeE: 55863.82<br />rentE: 1370.6585<br />popE: 1","incomeE: 56432.62<br />rentE: 1384.3413<br />popE: 1","incomeE: 57001.42<br />rentE: 1398.0240<br />popE: 1","incomeE: 57570.22<br />rentE: 1411.7067<br />popE: 1","incomeE: 58139.01<br />rentE: 1425.3895<br />popE: 1","incomeE: 58707.81<br />rentE: 1439.0722<br />popE: 1","incomeE: 59276.61<br />rentE: 1452.7549<br />popE: 1","incomeE: 59845.41<br />rentE: 1466.4377<br />popE: 1","incomeE: 60414.20<br />rentE: 1480.1204<br />popE: 1","incomeE: 60983.00<br />rentE: 1493.8032<br />popE: 1"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(255,140,0,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":49.813200498132},"plot_bgcolor":"rgba(255,255,255,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[13801.25,63229.75],"tickmode":"array","ticktext":["20000","30000","40000","50000","60000"],"tickvals":[20000,30000,40000,50000,60000],"categoryorder":"array","categoryarray":["20000","30000","40000","50000","60000"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":"<b> Median Household earnings <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[305.15,2193.85],"tickmode":"array","ticktext":["500","1000","1500","2000"],"tickvals":[500,1000,1500,2000],"categoryorder":"array","categoryarray":["500","1000","1500","2000"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(201,201,201,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":"<b> Median Gross Rent <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":1100,"height":500,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"3718fd111d5":{"x":{},"y":{},"label":{},"size":{},"type":"scatter"},"371819045c8a":{"x":{},"y":{},"label":{},"size":{}}},"cur_data":"3718fd111d5","visdat":{"3718fd111d5":["function (y) ","x"],"371819045c8a":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> --- # Amenities and Income I <div id="htmlwidget-46d8f6a36ed5c09ec508" style="width:1100px;height:500px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-46d8f6a36ed5c09ec508">{"x":{"data":[{"x":[32.5,31.2,33.8,50.3,48.2,59.3,65.1,60.3,53.5,51.4,63,51,46.4,54.7,55.2,59.6,57.3,60.5,55.7,62,47.7,57.6,53,63.2,66.3,46.4,57.4,58.8,64.4,56,57.1,57.8,53.5,61.6,46.4,58.4,56.9,54.9,55.9,36.5,42.6,38.1,46.3,36.6,39.8,39.3,37.7,42.6,39.5,38.8,38.4,39.7,37.7,38.5,38.6,38.2,39.7,43.8,46,43,39.7,37.4,43.4,36.2,37.3,27.3,36.7,33.4,22.9,23.6,20.3,22.4,20.9,21.6,21.2,22.9,21,20.5,22,23.9,27.8,23.1,21.3,29.1,25.3,23.9,21.9,19.5,23.7,29.3,24.7,23.9,23.3,22.9,24.1,22.9,23.4,24.6,23.8,24,23.5,23.5,21.7,28.5,24.7,16.6,19.5,18.1,19.9,21.3,17.6,28,28.5,32.4,28.2,28.7,28.8,29.7,29.2,30.6,28.8,31.8,46.1,42.6,42.9,46.6,45.4,48.3,45.4,45.5,47.6,41.1,43.6,46.4,45.5,48.9,18.2,19.5,18.2,16.4,19.9,33.1,30.2,29.2,30.2,32.9,30.3,29.3,30.9,31.4,32.6,32.8,29.9,33.8,32.5,30.2,20.2,27.9,24.6,23.3,22.2,24.9,26.6,28.1,27.4,23.8,24.5,22.4,24.8,23.5,23.5,22.2,23.4,23.4,23.6,23.8,22.5,23.7,24.9,25.1,22.5,25.2,22.7,23,23.1,24,12.8,14.2,14,14.4,12.9,14.2,6.3,14.6,12.6,13.3,13.8,36.2,45,42,45.8,40.7,41.1,28.1,29.1,27.4,28.5,30.4,28.2,31.9,29.5,28.6,29.4,30,24.6,28.8,22.4,21.9,22.2,21.8,50.5,38.2,22.5,20.1,22.8,20.3,31.8,28.4,31.5,32,31.8,29,31.9,31,26.5,29.3,29.4,29.8,25.6,30.6,25.5,28.1,22.9,29.8,24.6,35.5,42.5,33.6,34.6,32.8,21.2,30.7,20.8,21.3,23.7,22.2,17.2,31.3,23,30.3,31.1,23.5,17.2,20,21.9,23.7,19.4,30.8,21.5,31,26.3,15,19.8,20.6,29.4,19.3,21.9,27.2,35.3,41,30.6,36,34.7,39.8,38.4,34.8,35.2,34.1,36.3,34.9,37.5,31.9,34.1,37.4,36.8,41,40.2,35,37.6,35.9,39.2,34.8,37.2,36.5,37.8,10.7,24.6,26.4,23.9,28.1,22.5,25.6,25.3,26.1,26,25.3,28,25.6,24.6,24,25.6,23.3,24.1,24.9,25.2,24.3,23.5,24.7,25.4,23.4,26.7,23.8,25.4,37.2,38.8,39.2,37.8,36.2,40,34.5,42.6,40.8,42,41.4,41.9,42.9,43,44.1,27.5,25,22.9,26.1,24,27.9,21.4,21.6,21.8,29,27.4,26.2,31.1,22.4,24,27.9,21.7,27.8,26.3,26.7,21.6,21.7,22.1,22.5,28.6,25.8,31.8,23,24.8,24.1,27.7,27.5,26.8,28.2,42.3,39,45.3,43,44.3,43.9,40.9,37.5,40.9,41.4,37.8,41.2,37.6,40.4,36.8,15.8,23.3,32.7,34.8,33.9,34.8,32.6,33.3,33.7,35.4,31.8,32.4,32,33.5,33.3,44.6,47.9,49.3,46.1,56.7,41.4,46.4,43.4,42,44.3,43,44.7,48.5,49.1,40.4,41.8,47.2,48.2,45.9,54.7,47.5,42.1,42.3,38.7,43.9,44,46.8,53.7,42.1,38.2,37.1,42.3,42.9,41.7,43.3,46.5,51.4,40.9,45.7,29.7,34.9,35.1,32,41.8,31.6,17.7,32.9,32.8,33.7,32.3,33.8,34.4,31,32.1,31.3,30.7,33.4,36.3,36.4,36.2,37,34.3,36.5,37.8,43.2,42,39.3,43.5,39.1,36.7,38,34,42.2,34.6,34.3,30,29.5,26,19.5,19.3,14,18.7,22.4,16.7,14.3,22.7,18.2,21.8,19.1,20.2,20.2,18.7,20.5,18.7],"y":[37882,45562,36411,36764,32686,35363,35764,28959,28318,38223,31915,36465,33501,30831,32131,24468,37614,30186,32208,32119,38672,33697,28959,36042,30942,36100,33729,28293,36094,36715,35960,31997,44316,31179,38664,34930,40277,24968,31596,36229,31913,35768,35462,46798,29343,30613,45399,43213,43109,39836,38843,52496,56836,46267,38548,33993,40849,38724,32008,32202,34503,41527,29954,31531,40266,33449,30245,33038,39410,42020,39335,51976,41864,40052,49771,49427,36750,48186,46177,36729,40951,37544,35739,38047,41551,40650,49295,35796,36376,37437,34130,35636,56175,46883,42547,39030,34252,33192,35423,34456,43661,35957,36393,34595,32307,36997,44520,41925,42312,40250,36453,40648,50865,38080,38805,31620,44683,37021,36339,37886,40352,34855,50141,40410,31446,36175,38778,36953,38716,42582,34491,32834,33434,41829,35547,36759,35824,42029,36514,34410,40135,55749,48706,53584,46475,59163,53894,52486,68031,58114,47159,57265,40539,36708,40272,41270,38137,45556,48466,40640,44534,58185,59925,51090,46673,47839,38533,33253,33999,34015,39550,33774,37349,34985,38572,37174,48923,40719,41735,32965,50945,40409,32882,37087,47332,35242,47044,55410,50360,48465,47688,41105,38743,53232,39668,53765,47473,40183,31809,31431,36389,44810,40730,38115,42272,42296,36805,33985,38187,32432,39501,48325,43292,35072,38476,31705,37085,41275,39608,46780,36019,37950,47710,44067,51703,42861,36696,56098,52148,44106,30076,41763,52078,44506,64396,49889,52262,55930,63875,44400,41262,63975,52683,45318,48561,35316,26939,36462,33071,36281,47169,31161,36057,32444,46372,41034,35324,41099,40579,57312,64658,39932,36796,42274,41231,46727,36640,40152,45052,52443,49674,35168,51099,40336,51773,40882,39589,54439,34264,30259,33409,40630,33224,32526,32244,33980,40353,35963,34617,35681,35417,33770,37890,36006,41635,36966,33516,44099,35598,32300,29714,33564,42845,46449,30997,41714,33644,41391,33574,41377,31581,38078,61087,42355,40276,45287,40412,41632,40636,38575,35960,32416,45313,39397,36408,38869,32764,35533,39203,33778,52871,35562,41395,40383,39704,33843,35864,36920,45891,35912,31076,31589,31855,35117,32549,40109,45179,36140,39267,42344,39826,40310,33784,51417,45016,33474,39859,55456,43461,40170,46371,35100,34829,37968,36760,39843,36824,40659,35841,35013,33686,38567,53315,41590,36467,36430,40891,40484,40860,46012,40535,50155,35025,34812,33900,37644,40913,40158,31971,37306,29624,38853,34159,36374,33488,30817,40506,38132,33433,34613,34055,37562,36742,37349,36715,40292,35484,31445,39822,34163,59393,42043,35040,35006,50819,36434,25296,55869,42837,36727,50327,40711,42516,29741,53367,45465,35035,32259,41585,39299,41206,25670,37310,41002,40838,35288,32681,49514,48141,35753,43595,30896,42879,35355,41084,33079,33785,43878,27948,32583,47186,35042,43904,40040,39979,31913,37190,44765,45865,76895,46503,63997,51545,43428,71746,52944,46588,57312,62582,44158,37262,35947,34482,34440,42279,41968,43100,36217,54346,43035,42955,38704,49108,36896,44021,38282,30790,40062,34722,38805,40155,46181,38448,39457,40031,39583,39282,37331,41618,40753,36655,40266,38168,47597,51945,40245],"text":["Value: 32.5<br />incomeE: 37882<br />NAME: Kent County, Delaware<br />popE: 174822","Value: 31.2<br />incomeE: 45562<br />NAME: New Castle County, Delaware<br />popE: 555133","Value: 33.8<br />incomeE: 36411<br />NAME: Sussex County, Delaware<br />popE: 219540","Value: 50.3<br />incomeE: 36764<br />NAME: Alachua County, Florida<br />popE: 263148","Value: 48.2<br />incomeE: 32686<br />NAME: Bay County, Florida<br />popE: 182482","Value: 59.3<br />incomeE: 35363<br />NAME: Brevard County, Florida<br />popE: 576808","Value: 65.1<br />incomeE: 35764<br />NAME: Broward County, Florida<br />popE: 1909151","Value: 60.3<br />incomeE: 28959<br />NAME: Charlotte County, Florida<br />popE: 176954","Value: 53.5<br />incomeE: 28318<br />NAME: Citrus County, Florida<br />popE: 143087","Value: 51.4<br />incomeE: 38223<br />NAME: Clay County, Florida<br />popE: 207291","Value: 63.0<br />incomeE: 31915<br />NAME: Collier County, Florida<br />popE: 363922","Value: 51.0<br />incomeE: 36465<br />NAME: Duval County, Florida<br />popE: 924229","Value: 46.4<br />incomeE: 33501<br />NAME: Escambia County, Florida<br />popE: 311522","Value: 54.7<br />incomeE: 30831<br />NAME: Flagler County, Florida<br />popE: 107139","Value: 55.2<br />incomeE: 32131<br />NAME: Hernando County, Florida<br />popE: 182696","Value: 59.6<br />incomeE: 24468<br />NAME: Highlands County, Florida<br />popE: 102101","Value: 57.3<br />incomeE: 37614<br />NAME: Hillsborough County, Florida<br />popE: 1378883","Value: 60.5<br />incomeE: 30186<br />NAME: Indian River County, Florida<br />popE: 150984","Value: 55.7<br />incomeE: 32208<br />NAME: Lake County, Florida<br />popE: 335362","Value: 62.0<br />incomeE: 32119<br />NAME: Lee County, Florida<br />popE: 718679","Value: 47.7<br />incomeE: 38672<br />NAME: Leon County, Florida<br />popE: 288102","Value: 57.6<br />incomeE: 33697<br />NAME: Manatee County, Florida<br />popE: 373853","Value: 53.0<br />incomeE: 28959<br />NAME: Marion County, Florida<br />popE: 348371","Value: 63.2<br />incomeE: 36042<br />NAME: Martin County, Florida<br />popE: 157581","Value: 66.3<br />incomeE: 30942<br />NAME: Miami-Dade County, Florida<br />popE: 2715516","Value: 46.4<br />incomeE: 36100<br />NAME: Okaloosa County, Florida<br />popE: 200737","Value: 57.4<br />incomeE: 33729<br />NAME: Orange County, Florida<br />popE: 1321194","Value: 58.8<br />incomeE: 28293<br />NAME: Osceola County, Florida<br />popE: 338619","Value: 64.4<br />incomeE: 36094<br />NAME: Palm Beach County, Florida<br />popE: 1446277","Value: 56.0<br />incomeE: 36715<br />NAME: Pasco County, Florida<br />popE: 510593","Value: 57.1<br />incomeE: 35960<br />NAME: Pinellas County, Florida<br />popE: 957875","Value: 57.8<br />incomeE: 31997<br />NAME: Polk County, Florida<br />popE: 668671","Value: 53.5<br />incomeE: 44316<br />NAME: St. Johns County, Florida<br />popE: 235503","Value: 61.6<br />incomeE: 31179<br />NAME: St. Lucie County, Florida<br />popE: 305591","Value: 46.4<br />incomeE: 38664<br />NAME: Santa Rosa County, Florida<br />popE: 170442","Value: 58.4<br />incomeE: 34930<br />NAME: Sarasota County, Florida<br />popE: 412144","Value: 56.9<br />incomeE: 40277<br />NAME: Seminole County, Florida<br />popE: 455086","Value: 54.9<br />incomeE: 24968<br />NAME: Sumter County, Florida<br />popE: 120999","Value: 55.9<br />incomeE: 31596<br />NAME: Volusia County, Florida<br />popE: 527634","Value: 36.5<br />incomeE: 36229<br />NAME: Bartow County, Georgia<br />popE: 103620","Value: 42.6<br />incomeE: 31913<br />NAME: Bibb County, Georgia<br />popE: 153490","Value: 38.1<br />incomeE: 35768<br />NAME: Carroll County, Georgia<br />popE: 116022","Value: 46.3<br />incomeE: 35462<br />NAME: Chatham County, Georgia<br />popE: 287049","Value: 36.6<br />incomeE: 46798<br />NAME: Cherokee County, Georgia<br />popE: 241910","Value: 39.8<br />incomeE: 29343<br />NAME: Clarke County, Georgia<br />popE: 124602","Value: 39.3<br />incomeE: 30613<br />NAME: Clayton County, Georgia<br />popE: 278666","Value: 37.7<br />incomeE: 45399<br />NAME: Cobb County, Georgia<br />popE: 745057","Value: 42.6<br />incomeE: 43213<br />NAME: Columbia County, Georgia<br />popE: 147295","Value: 39.5<br />incomeE: 43109<br />NAME: Coweta County, Georgia<br />popE: 140516","Value: 38.8<br />incomeE: 39836<br />NAME: DeKalb County, Georgia<br />popE: 743187","Value: 38.4<br />incomeE: 38843<br />NAME: Douglas County, Georgia<br />popE: 141840","Value: 39.7<br />incomeE: 52496<br />NAME: Fayette County, Georgia<br />popE: 111369","Value: 37.7<br />incomeE: 56836<br />NAME: Forsyth County, Georgia<br />popE: 219880","Value: 38.5<br />incomeE: 46267<br />NAME: Fulton County, Georgia<br />popE: 1021902","Value: 38.6<br />incomeE: 38548<br />NAME: Gwinnett County, Georgia<br />popE: 902298","Value: 38.2<br />incomeE: 33993<br />NAME: Hall County, Georgia<br />popE: 195961","Value: 39.7<br />incomeE: 40849<br />NAME: Henry County, Georgia<br />popE: 221307","Value: 43.8<br />incomeE: 38724<br />NAME: Houston County, Georgia<br />popE: 151682","Value: 46.0<br />incomeE: 32008<br />NAME: Lowndes County, Georgia<br />popE: 114582","Value: 43.0<br />incomeE: 32202<br />NAME: Muscogee County, Georgia<br />popE: 196670","Value: 39.7<br />incomeE: 34503<br />NAME: Newton County, Georgia<br />popE: 106497","Value: 37.4<br />incomeE: 41527<br />NAME: Paulding County, Georgia<br />popE: 155840","Value: 43.4<br />incomeE: 29954<br />NAME: Richmond County, Georgia<br />popE: 201463","Value: 36.2<br />incomeE: 31531<br />NAME: Whitfield County, Georgia<br />popE: 103849","Value: 37.3<br />incomeE: 40266<br />NAME: Ada County, Idaho<br />popE: 446052","Value: 27.3<br />incomeE: 33449<br />NAME: Bonneville County, Idaho<br />popE: 112397","Value: 36.7<br />incomeE: 30245<br />NAME: Canyon County, Idaho<br />popE: 212230","Value: 33.4<br />incomeE: 33038<br />NAME: Kootenai County, Idaho<br />popE: 153605","Value: 22.9<br />incomeE: 39410<br />NAME: Champaign County, Illinois<br />popE: 209448","Value: 23.6<br />incomeE: 42020<br />NAME: Cook County, Illinois<br />popE: 5223719","Value: 20.3<br />incomeE: 39335<br />NAME: DeKalb County, Illinois<br />popE: 104200","Value: 22.4<br />incomeE: 51976<br />NAME: DuPage County, Illinois<br />popE: 931743","Value: 20.9<br />incomeE: 41864<br />NAME: Kane County, Illinois<br />popE: 530839","Value: 21.6<br />incomeE: 40052<br />NAME: Kankakee County, Illinois<br />popE: 111061","Value: 21.2<br />incomeE: 49771<br />NAME: Kendall County, Illinois<br />popE: 124626","Value: 22.9<br />incomeE: 49427<br />NAME: Lake County, Illinois<br />popE: 703619","Value: 21.0<br />incomeE: 36750<br />NAME: LaSalle County, Illinois<br />popE: 110401","Value: 20.5<br />incomeE: 48186<br />NAME: McHenry County, Illinois<br />popE: 307789","Value: 22.0<br />incomeE: 46177<br />NAME: McLean County, Illinois<br />popE: 173219","Value: 23.9<br />incomeE: 36729<br />NAME: Macon County, Illinois<br />popE: 106512","Value: 27.8<br />incomeE: 40951<br />NAME: Madison County, Illinois<br />popE: 265670","Value: 23.1<br />incomeE: 37544<br />NAME: Peoria County, Illinois<br />popE: 184463","Value: 21.3<br />incomeE: 35739<br />NAME: Rock Island County, Illinois<br />popE: 145275","Value: 29.1<br />incomeE: 38047<br />NAME: St. Clair County, Illinois<br />popE: 263463","Value: 25.3<br />incomeE: 41551<br />NAME: Sangamon County, Illinois<br />popE: 197661","Value: 23.9<br />incomeE: 40650<br />NAME: Tazewell County, Illinois<br />popE: 133852","Value: 21.9<br />incomeE: 49295<br />NAME: Will County, Illinois<br />popE: 688697","Value: 19.5<br />incomeE: 35796<br />NAME: Winnebago County, Illinois<br />popE: 286174","Value: 23.7<br />incomeE: 36376<br />NAME: Allen County, Indiana<br />popE: 370016","Value: 29.3<br />incomeE: 37437<br />NAME: Clark County, Indiana<br />popE: 115702","Value: 24.7<br />incomeE: 34130<br />NAME: Delaware County, Indiana<br />popE: 115616","Value: 23.9<br />incomeE: 35636<br />NAME: Elkhart County, Indiana<br />popE: 203604","Value: 23.3<br />incomeE: 56175<br />NAME: Hamilton County, Indiana<br />popE: 316095","Value: 22.9<br />incomeE: 46883<br />NAME: Hendricks County, Indiana<br />popE: 160940","Value: 24.1<br />incomeE: 42547<br />NAME: Johnson County, Indiana<br />popE: 151564","Value: 22.9<br />incomeE: 39030<br />NAME: Lake County, Indiana<br />popE: 486849","Value: 23.4<br />incomeE: 34252<br />NAME: LaPorte County, Indiana<br />popE: 110552","Value: 24.6<br />incomeE: 33192<br />NAME: Madison County, Indiana<br />popE: 129505","Value: 23.8<br />incomeE: 35423<br />NAME: Marion County, Indiana<br />popE: 944523","Value: 24.0<br />incomeE: 34456<br />NAME: Monroe County, Indiana<br />popE: 145403","Value: 23.5<br />incomeE: 43661<br />NAME: Porter County, Indiana<br />popE: 168041","Value: 23.5<br />incomeE: 35957<br />NAME: St. Joseph County, Indiana<br />popE: 269240","Value: 21.7<br />incomeE: 36393<br />NAME: Tippecanoe County, Indiana<br />popE: 189294","Value: 28.5<br />incomeE: 34595<br />NAME: Vanderburgh County, Indiana<br />popE: 181313","Value: 24.7<br />incomeE: 32307<br />NAME: Vigo County, Indiana<br />popE: 107693","Value: 16.6<br />incomeE: 36997<br />NAME: Black Hawk County, Iowa<br />popE: 133009","Value: 19.5<br />incomeE: 44520<br />NAME: Johnson County, Iowa<br />popE: 147001","Value: 18.1<br />incomeE: 41925<br />NAME: Linn County, Iowa<br />popE: 222121","Value: 19.9<br />incomeE: 42312<br />NAME: Polk County, Iowa<br />popE: 474274","Value: 21.3<br />incomeE: 40250<br />NAME: Scott County, Iowa<br />popE: 172288","Value: 17.6<br />incomeE: 36453<br />NAME: Woodbury County, Iowa<br />popE: 102398","Value: 28.0<br />incomeE: 40648<br />NAME: Douglas County, Kansas<br />popE: 119319","Value: 28.5<br />incomeE: 50865<br />NAME: Johnson County, Kansas<br />popE: 585502","Value: 32.4<br />incomeE: 38080<br />NAME: Sedgwick County, Kansas<br />popE: 512064","Value: 28.2<br />incomeE: 38805<br />NAME: Shawnee County, Kansas<br />popE: 178284","Value: 28.7<br />incomeE: 31620<br />NAME: Wyandotte County, Kansas<br />popE: 164345","Value: 28.8<br />incomeE: 44683<br />NAME: Boone County, Kentucky<br />popE: 129095","Value: 29.7<br />incomeE: 37021<br />NAME: Fayette County, Kentucky<br />popE: 318734","Value: 29.2<br />incomeE: 36339<br />NAME: Hardin County, Kentucky<br />popE: 108095","Value: 30.6<br />incomeE: 37886<br />NAME: Jefferson County, Kentucky<br />popE: 767154","Value: 28.8<br />incomeE: 40352<br />NAME: Kenton County, Kentucky<br />popE: 164688","Value: 31.8<br />incomeE: 34855<br />NAME: Warren County, Kentucky<br />popE: 126427","Value: 46.1<br />incomeE: 50141<br />NAME: Ascension Parish, Louisiana<br />popE: 121176","Value: 42.6<br />incomeE: 40410<br />NAME: Bossier Parish, Louisiana<br />popE: 126131","Value: 42.9<br />incomeE: 31446<br />NAME: Caddo Parish, Louisiana<br />popE: 248361","Value: 46.6<br />incomeE: 36175<br />NAME: Calcasieu Parish, Louisiana<br />popE: 200182","Value: 45.4<br />incomeE: 38778<br />NAME: East Baton Rouge Parish, Louisiana<br />popE: 444094","Value: 48.3<br />incomeE: 36953<br />NAME: Jefferson Parish, Louisiana<br />popE: 435300","Value: 45.4<br />incomeE: 38716<br />NAME: Lafayette Parish, Louisiana<br />popE: 240091","Value: 45.5<br />incomeE: 42582<br />NAME: Livingston Parish, Louisiana<br />popE: 138111","Value: 47.6<br />incomeE: 34491<br />NAME: Orleans Parish, Louisiana<br />popE: 389648","Value: 41.1<br />incomeE: 32834<br />NAME: Ouachita Parish, Louisiana<br />popE: 156075","Value: 43.6<br />incomeE: 33434<br />NAME: Rapides Parish, Louisiana<br />popE: 131546","Value: 46.4<br />incomeE: 41829<br />NAME: St. Tammany Parish, Louisiana<br />popE: 252093","Value: 45.5<br />incomeE: 35547<br />NAME: Tangipahoa Parish, Louisiana<br />popE: 130504","Value: 48.9<br />incomeE: 36759<br />NAME: Terrebonne Parish, Louisiana<br />popE: 112587","Value: 18.2<br />incomeE: 35824<br />NAME: Androscoggin County, Maine<br />popE: 107444","Value: 19.5<br />incomeE: 42029<br />NAME: Cumberland County, Maine<br />popE: 290944","Value: 18.2<br />incomeE: 36514<br />NAME: Kennebec County, Maine<br />popE: 121545","Value: 16.4<br />incomeE: 34410<br />NAME: Penobscot County, Maine<br />popE: 151748","Value: 19.9<br />incomeE: 40135<br />NAME: York County, Maine<br />popE: 203102","Value: 33.1<br />incomeE: 55749<br />NAME: Anne Arundel County, Maryland<br />popE: 567696","Value: 30.2<br />incomeE: 48706<br />NAME: Baltimore County, Maryland<br />popE: 827625","Value: 29.2<br />incomeE: 53584<br />NAME: Carroll County, Maryland<br />popE: 167522","Value: 30.2<br />incomeE: 46475<br />NAME: Cecil County, Maryland<br />popE: 102517","Value: 32.9<br />incomeE: 59163<br />NAME: Charles County, Maryland<br />popE: 157671","Value: 30.3<br />incomeE: 53894<br />NAME: Frederick County, Maryland<br />popE: 248472","Value: 29.3<br />incomeE: 52486<br />NAME: Harford County, Maryland<br />popE: 251025","Value: 30.9<br />incomeE: 68031<br />NAME: Howard County, Maryland<br />popE: 315327","Value: 31.4<br />incomeE: 58114<br />NAME: Montgomery County, Maryland<br />popE: 1040133","Value: 32.6<br />incomeE: 47159<br />NAME: Prince George's County, Maryland<br />popE: 906202","Value: 32.8<br />incomeE: 57265<br />NAME: St. Mary's County, Maryland<br />popE: 111531","Value: 29.9<br />incomeE: 40539<br />NAME: Washington County, Maryland<br />popE: 149811","Value: 33.8<br />incomeE: 36708<br />NAME: Wicomico County, Maryland<br />popE: 102172","Value: 32.5<br />incomeE: 40272<br />NAME: Baltimore city, Maryland<br />popE: 614700","Value: 30.2<br />incomeE: 41270<br />NAME: Barnstable County, Massachusetts<br />popE: 213690","Value: 20.2<br />incomeE: 38137<br />NAME: Berkshire County, Massachusetts<br />popE: 127328","Value: 27.9<br />incomeE: 45556<br />NAME: Bristol County, Massachusetts<br />popE: 558905","Value: 24.6<br />incomeE: 48466<br />NAME: Essex County, Massachusetts<br />popE: 781024","Value: 23.3<br />incomeE: 40640<br />NAME: Hampden County, Massachusetts<br />popE: 469116","Value: 22.2<br />incomeE: 44534<br />NAME: Hampshire County, Massachusetts<br />popE: 161159","Value: 24.9<br />incomeE: 58185<br />NAME: Middlesex County, Massachusetts<br />popE: 1595192","Value: 26.6<br />incomeE: 59925<br />NAME: Norfolk County, Massachusetts<br />popE: 698249","Value: 28.1<br />incomeE: 51090<br />NAME: Plymouth County, Massachusetts<br />popE: 512135","Value: 27.4<br />incomeE: 46673<br />NAME: Suffolk County, Massachusetts<br />popE: 791766","Value: 23.8<br />incomeE: 47839<br />NAME: Worcester County, Massachusetts<br />popE: 822280","Value: 24.5<br />incomeE: 38533<br />NAME: Allegan County, Michigan<br />popE: 115250","Value: 22.4<br />incomeE: 33253<br />NAME: Bay County, Michigan<br />popE: 104786","Value: 24.8<br />incomeE: 33999<br />NAME: Berrien County, Michigan<br />popE: 154807","Value: 23.5<br />incomeE: 34015<br />NAME: Calhoun County, Michigan<br />popE: 134473","Value: 23.5<br />incomeE: 39550<br />NAME: Eaton County, Michigan<br />popE: 109155","Value: 22.2<br />incomeE: 33774<br />NAME: Genesee County, Michigan<br />popE: 409361","Value: 23.4<br />incomeE: 37349<br />NAME: Ingham County, Michigan<br />popE: 289564","Value: 23.4<br />incomeE: 34985<br />NAME: Jackson County, Michigan<br />popE: 158913","Value: 23.6<br />incomeE: 38572<br />NAME: Kalamazoo County, Michigan<br />popE: 261573","Value: 23.8<br />incomeE: 37174<br />NAME: Kent County, Michigan<br />popE: 643140","Value: 22.5<br />incomeE: 48923<br />NAME: Livingston County, Michigan<br />popE: 188482","Value: 23.7<br />incomeE: 40719<br />NAME: Macomb County, Michigan<br />popE: 868704","Value: 24.9<br />incomeE: 41735<br />NAME: Monroe County, Michigan<br />popE: 149699","Value: 25.1<br />incomeE: 32965<br />NAME: Muskegon County, Michigan<br />popE: 173043","Value: 22.5<br />incomeE: 50945<br />NAME: Oakland County, Michigan<br />popE: 1250843","Value: 25.2<br />incomeE: 40409<br />NAME: Ottawa County, Michigan<br />popE: 284034","Value: 22.7<br />incomeE: 32882<br />NAME: Saginaw County, Michigan<br />popE: 192778","Value: 23.0<br />incomeE: 37087<br />NAME: St. Clair County, Michigan<br />popE: 159566","Value: 23.1<br />incomeE: 47332<br />NAME: Washtenaw County, Michigan<br />popE: 365961","Value: 24.0<br />incomeE: 35242<br />NAME: Wayne County, Michigan<br />popE: 1761382","Value: 12.8<br />incomeE: 47044<br />NAME: Anoka County, Minnesota<br />popE: 347431","Value: 14.2<br />incomeE: 55410<br />NAME: Carver County, Minnesota<br />popE: 100416","Value: 14.0<br />incomeE: 50360<br />NAME: Dakota County, Minnesota<br />popE: 418201","Value: 14.4<br />incomeE: 48465<br />NAME: Hennepin County, Minnesota<br />popE: 1235478","Value: 12.9<br />incomeE: 47688<br />NAME: Olmsted County, Minnesota<br />popE: 153065","Value: 14.2<br />incomeE: 41105<br />NAME: Ramsey County, Minnesota<br />popE: 541493","Value: 6.3<br />incomeE: 38743<br />NAME: St. Louis County, Minnesota<br />popE: 200080","Value: 14.6<br />incomeE: 53232<br />NAME: Scott County, Minnesota<br />popE: 143372","Value: 12.6<br />incomeE: 39668<br />NAME: Stearns County, Minnesota<br />popE: 156819","Value: 13.3<br />incomeE: 53765<br />NAME: Washington County, Minnesota<br />popE: 253317","Value: 13.8<br />incomeE: 47473<br />NAME: Wright County, Minnesota<br />popE: 132745","Value: 36.2<br />incomeE: 40183<br />NAME: DeSoto County, Mississippi<br />popE: 176132","Value: 45.0<br />incomeE: 31809<br />NAME: Harrison County, Mississippi<br />popE: 202626","Value: 42.0<br />incomeE: 31431<br />NAME: Hinds County, Mississippi<br />popE: 241774","Value: 45.8<br />incomeE: 36389<br />NAME: Jackson County, Mississippi<br />popE: 142014","Value: 40.7<br />incomeE: 44810<br />NAME: Madison County, Mississippi<br />popE: 103498","Value: 41.1<br />incomeE: 40730<br />NAME: Rankin County, Mississippi<br />popE: 151240","Value: 28.1<br />incomeE: 38115<br />NAME: Boone County, Missouri<br />popE: 176515","Value: 29.1<br />incomeE: 42272<br />NAME: Cass County, Missouri<br />popE: 102678","Value: 27.4<br />incomeE: 42296<br />NAME: Clay County, Missouri<br />popE: 239164","Value: 28.5<br />incomeE: 36805<br />NAME: Franklin County, Missouri<br />popE: 102781","Value: 30.4<br />incomeE: 33985<br />NAME: Greene County, Missouri<br />popE: 288429","Value: 28.2<br />incomeE: 38187<br />NAME: Jackson County, Missouri<br />popE: 692003","Value: 31.9<br />incomeE: 32432<br />NAME: Jasper County, Missouri<br />popE: 119238","Value: 29.5<br />incomeE: 39501<br />NAME: Jefferson County, Missouri<br />popE: 223302","Value: 28.6<br />incomeE: 48325<br />NAME: St. Charles County, Missouri<br />popE: 389985","Value: 29.4<br />incomeE: 43292<br />NAME: St. Louis County, Missouri<br />popE: 998684","Value: 30.0<br />incomeE: 35072<br />NAME: St. Louis city, Missouri<br />popE: 311273","Value: 24.6<br />incomeE: 38476<br />NAME: Gallatin County, Montana<br />popE: 104729","Value: 28.8<br />incomeE: 31705<br />NAME: Missoula County, Montana<br />popE: 115983","Value: 22.4<br />incomeE: 37085<br />NAME: Yellowstone County, Montana<br />popE: 157816","Value: 21.9<br />incomeE: 41275<br />NAME: Douglas County, Nebraska<br />popE: 554992","Value: 22.2<br />incomeE: 39608<br />NAME: Lancaster County, Nebraska<br />popE: 310094","Value: 21.8<br />incomeE: 46780<br />NAME: Sarpy County, Nebraska<br />popE: 178351","Value: 50.5<br />incomeE: 36019<br />NAME: Clark County, Nevada<br />popE: 2141574","Value: 38.2<br />incomeE: 37950<br />NAME: Washoe County, Nevada<br />popE: 450486","Value: 22.5<br />incomeE: 47710<br />NAME: Hillsborough County, New Hampshire<br />popE: 411087","Value: 20.1<br />incomeE: 44067<br />NAME: Merrimack County, New Hampshire<br />popE: 149452","Value: 22.8<br />incomeE: 51703<br />NAME: Rockingham County, New Hampshire<br />popE: 305129","Value: 20.3<br />incomeE: 42861<br />NAME: Strafford County, New Hampshire<br />popE: 128237","Value: 31.8<br />incomeE: 36696<br />NAME: Atlantic County, New Jersey<br />popE: 268539","Value: 28.4<br />incomeE: 56098<br />NAME: Bergen County, New Jersey<br />popE: 929999","Value: 31.5<br />incomeE: 52148<br />NAME: Burlington County, New Jersey<br />popE: 446367","Value: 32.0<br />incomeE: 44106<br />NAME: Camden County, New Jersey<br />popE: 507367","Value: 31.8<br />incomeE: 30076<br />NAME: Cumberland County, New Jersey<br />popE: 153400","Value: 29.0<br />incomeE: 41763<br />NAME: Essex County, New Jersey<br />popE: 793555","Value: 31.9<br />incomeE: 52078<br />NAME: Gloucester County, New Jersey<br />popE: 290852","Value: 31.0<br />incomeE: 44506<br />NAME: Hudson County, New Jersey<br />popE: 668631","Value: 26.5<br />incomeE: 64396<br />NAME: Hunterdon County, New Jersey<br />popE: 125051","Value: 29.3<br />incomeE: 49889<br />NAME: Mercer County, New Jersey<br />popE: 368762","Value: 29.4<br />incomeE: 52262<br />NAME: Middlesex County, New Jersey<br />popE: 826698","Value: 29.8<br />incomeE: 55930<br />NAME: Monmouth County, New Jersey<br />popE: 623387","Value: 25.6<br />incomeE: 63875<br />NAME: Morris County, New Jersey<br />popE: 494383","Value: 30.6<br />incomeE: 44400<br />NAME: Ocean County, New Jersey<br />popE: 591939","Value: 25.5<br />incomeE: 41262<br />NAME: Passaic County, New Jersey<br />popE: 504041","Value: 28.1<br />incomeE: 63975<br />NAME: Somerset County, New Jersey<br />popE: 330176","Value: 22.9<br />incomeE: 52683<br />NAME: Sussex County, New Jersey<br />popE: 142298","Value: 29.8<br />incomeE: 45318<br />NAME: Union County, New Jersey<br />popE: 553066","Value: 24.6<br />incomeE: 48561<br />NAME: Warren County, New Jersey<br />popE: 106293","Value: 35.5<br />incomeE: 35316<br />NAME: Bernalillo County, New Mexico<br />popE: 677692","Value: 42.5<br />incomeE: 26939<br />NAME: Doña Ana County, New Mexico<br />popE: 215338","Value: 33.6<br />incomeE: 36462<br />NAME: Sandoval County, New Mexico<br />popE: 140769","Value: 34.6<br />incomeE: 33071<br />NAME: San Juan County, New Mexico<br />popE: 127455","Value: 32.8<br />incomeE: 36281<br />NAME: Santa Fe County, New Mexico<br />popE: 148917","Value: 21.2<br />incomeE: 47169<br />NAME: Albany County, New York<br />popE: 307426","Value: 30.7<br />incomeE: 31161<br />NAME: Bronx County, New York<br />popE: 1437872","Value: 20.8<br />incomeE: 36057<br />NAME: Broome County, New York<br />popE: 194402","Value: 21.3<br />incomeE: 32444<br />NAME: Chautauqua County, New York<br />popE: 129656","Value: 23.7<br />incomeE: 46372<br />NAME: Dutchess County, New York<br />popE: 293894","Value: 22.2<br />incomeE: 41034<br />NAME: Erie County, New York<br />popE: 919866","Value: 17.2<br />incomeE: 35324<br />NAME: Jefferson County, New York<br />popE: 114448","Value: 31.3<br />incomeE: 41099<br />NAME: Kings County, New York<br />popE: 2600747","Value: 23.0<br />incomeE: 40579<br />NAME: Monroe County, New York<br />popE: 744248","Value: 30.3<br />incomeE: 57312<br />NAME: Nassau County, New York<br />popE: 1356564","Value: 31.1<br />incomeE: 64658<br />NAME: New York County, New York<br />popE: 1632480","Value: 23.5<br />incomeE: 39932<br />NAME: Niagara County, New York<br />popE: 211704","Value: 17.2<br />incomeE: 36796<br />NAME: Oneida County, New York<br />popE: 230782","Value: 20.0<br />incomeE: 42274<br />NAME: Onondaga County, New York<br />popE: 464242","Value: 21.9<br />incomeE: 41231<br />NAME: Ontario County, New York<br />popE: 109472","Value: 23.7<br />incomeE: 46727<br />NAME: Orange County, New York<br />popE: 378227","Value: 19.4<br />incomeE: 36640<br />NAME: Oswego County, New York<br />popE: 119104","Value: 30.8<br />incomeE: 40152<br />NAME: Queens County, New York<br />popE: 2298513","Value: 21.5<br />incomeE: 45052<br />NAME: Rensselaer County, New York<br />popE: 159431","Value: 31.0<br />incomeE: 52443<br />NAME: Richmond County, New York<br />popE: 474101","Value: 26.3<br />incomeE: 49674<br />NAME: Rockland County, New York<br />popE: 323686","Value: 15.0<br />incomeE: 35168<br />NAME: St. Lawrence County, New York<br />popE: 109558","Value: 19.8<br />incomeE: 51099<br />NAME: Saratoga County, New York<br />popE: 227377","Value: 20.6<br />incomeE: 40336<br />NAME: Schenectady County, New York<br />popE: 154883","Value: 29.4<br />incomeE: 51773<br />NAME: Suffolk County, New York<br />popE: 1487901","Value: 19.3<br />incomeE: 40882<br />NAME: Tompkins County, New York<br />popE: 102962","Value: 21.9<br />incomeE: 39589<br />NAME: Ulster County, New York<br />popE: 179303","Value: 27.2<br />incomeE: 54439<br />NAME: Westchester County, New York<br />popE: 968815","Value: 35.3<br />incomeE: 34264<br />NAME: Alamance County, North Carolina<br />popE: 160576","Value: 41.0<br />incomeE: 30259<br />NAME: Brunswick County, North Carolina<br />popE: 126860","Value: 30.6<br />incomeE: 33409<br />NAME: Buncombe County, North Carolina<br />popE: 254474","Value: 36.0<br />incomeE: 40630<br />NAME: Cabarrus County, North Carolina<br />popE: 201448","Value: 34.7<br />incomeE: 33224<br />NAME: Catawba County, North Carolina<br />popE: 156729","Value: 39.8<br />incomeE: 32526<br />NAME: Craven County, North Carolina<br />popE: 103082","Value: 38.4<br />incomeE: 32244<br />NAME: Cumberland County, North Carolina<br />popE: 332106","Value: 34.8<br />incomeE: 33980<br />NAME: Davidson County, North Carolina<br />popE: 164664","Value: 35.2<br />incomeE: 40353<br />NAME: Durham County, North Carolina<br />popE: 306457","Value: 34.1<br />incomeE: 35963<br />NAME: Forsyth County, North Carolina<br />popE: 371573","Value: 36.3<br />incomeE: 34617<br />NAME: Gaston County, North Carolina<br />popE: 216585","Value: 34.9<br />incomeE: 35681<br />NAME: Guilford County, North Carolina<br />popE: 523582","Value: 37.5<br />incomeE: 35417<br />NAME: Harnett County, North Carolina<br />popE: 130361","Value: 31.9<br />incomeE: 33770<br />NAME: Henderson County, North Carolina<br />popE: 113625","Value: 34.1<br />incomeE: 37890<br />NAME: Iredell County, North Carolina<br />popE: 172525","Value: 37.4<br />incomeE: 36006<br />NAME: Johnston County, North Carolina<br />popE: 191172","Value: 36.8<br />incomeE: 41635<br />NAME: Mecklenburg County, North Carolina<br />popE: 1054314","Value: 41.0<br />incomeE: 36966<br />NAME: New Hanover County, North Carolina<br />popE: 224231","Value: 40.2<br />incomeE: 33516<br />NAME: Onslow County, North Carolina<br />popE: 193912","Value: 35.0<br />incomeE: 44099<br />NAME: Orange County, North Carolina<br />popE: 142938","Value: 37.6<br />incomeE: 35598<br />NAME: Pitt County, North Carolina<br />popE: 177372","Value: 35.9<br />incomeE: 32300<br />NAME: Randolph County, North Carolina<br />popE: 142958","Value: 39.2<br />incomeE: 29714<br />NAME: Robeson County, North Carolina<br />popE: 133442","Value: 34.8<br />incomeE: 33564<br />NAME: Rowan County, North Carolina<br />popE: 139605","Value: 37.2<br />incomeE: 42845<br />NAME: Union County, North Carolina<br />popE: 226694","Value: 36.5<br />incomeE: 46449<br />NAME: Wake County, North Carolina<br />popE: 1046558","Value: 37.8<br />incomeE: 30997<br />NAME: Wayne County, North Carolina<br />popE: 124002","Value: 10.7<br />incomeE: 41714<br />NAME: Cass County, North Dakota<br />popE: 174202","Value: 24.6<br />incomeE: 33644<br />NAME: Allen County, Ohio<br />popE: 103642","Value: 26.4<br />incomeE: 41391<br />NAME: Butler County, Ohio<br />popE: 378294","Value: 23.9<br />incomeE: 33574<br />NAME: Clark County, Ohio<br />popE: 135198","Value: 28.1<br />incomeE: 41377<br />NAME: Clermont County, Ohio<br />popE: 203216","Value: 22.5<br />incomeE: 31581<br />NAME: Columbiana County, Ohio<br />popE: 104003","Value: 25.6<br />incomeE: 38078<br />NAME: Cuyahoga County, Ohio<br />popE: 1253783","Value: 25.3<br />incomeE: 61087<br />NAME: Delaware County, Ohio<br />popE: 197008","Value: 26.1<br />incomeE: 42355<br />NAME: Fairfield County, Ohio<br />popE: 152910","Value: 26.0<br />incomeE: 40276<br />NAME: Franklin County, Ohio<br />popE: 1275333","Value: 25.3<br />incomeE: 45287<br />NAME: Greene County, Ohio<br />popE: 165811","Value: 28.0<br />incomeE: 40412<br />NAME: Hamilton County, Ohio<br />popE: 812037","Value: 25.6<br />incomeE: 41632<br />NAME: Lake County, Ohio<br />popE: 230052","Value: 24.6<br />incomeE: 40636<br />NAME: Licking County, Ohio<br />popE: 172293","Value: 24.0<br />incomeE: 38575<br />NAME: Lorain County, Ohio<br />popE: 306713","Value: 25.6<br />incomeE: 35960<br />NAME: Lucas County, Ohio<br />popE: 432379","Value: 23.3<br />incomeE: 32416<br />NAME: Mahoning County, Ohio<br />popE: 231064","Value: 24.1<br />incomeE: 45313<br />NAME: Medina County, Ohio<br />popE: 177257","Value: 24.9<br />incomeE: 39397<br />NAME: Miami County, Ohio<br />popE: 104800","Value: 25.2<br />incomeE: 36408<br />NAME: Montgomery County, Ohio<br />popE: 532034","Value: 24.3<br />incomeE: 38869<br />NAME: Portage County, Ohio<br />popE: 162644","Value: 23.5<br />incomeE: 32764<br />NAME: Richland County, Ohio<br />popE: 121324","Value: 24.7<br />incomeE: 35533<br />NAME: Stark County, Ohio<br />popE: 373475","Value: 25.4<br />incomeE: 39203<br />NAME: Summit County, Ohio<br />popE: 541810","Value: 23.4<br />incomeE: 33778<br />NAME: Trumbull County, Ohio<br />popE: 201794","Value: 26.7<br />incomeE: 52871<br />NAME: Warren County, Ohio<br />popE: 226564","Value: 23.8<br />incomeE: 35562<br />NAME: Wayne County, Ohio<br />popE: 116208","Value: 25.4<br />incomeE: 41395<br />NAME: Wood County, Ohio<br />popE: 129936","Value: 37.2<br />incomeE: 40383<br />NAME: Canadian County, Oklahoma<br />popE: 136710","Value: 38.8<br />incomeE: 39704<br />NAME: Cleveland County, Oklahoma<br />popE: 276733","Value: 39.2<br />incomeE: 33843<br />NAME: Comanche County, Oklahoma<br />popE: 122561","Value: 37.8<br />incomeE: 35864<br />NAME: Oklahoma County, Oklahoma<br />popE: 782051","Value: 36.2<br />incomeE: 36920<br />NAME: Tulsa County, Oklahoma<br />popE: 642781","Value: 40.0<br />incomeE: 45891<br />NAME: Clackamas County, Oregon<br />popE: 405788","Value: 34.5<br />incomeE: 35912<br />NAME: Deschutes County, Oregon<br />popE: 180640","Value: 42.6<br />incomeE: 31076<br />NAME: Douglas County, Oregon<br />popE: 108323","Value: 40.8<br />incomeE: 31589<br />NAME: Jackson County, Oregon<br />popE: 214267","Value: 42.0<br />incomeE: 31855<br />NAME: Lane County, Oregon<br />popE: 368882","Value: 41.4<br />incomeE: 35117<br />NAME: Linn County, Oregon<br />popE: 122870","Value: 41.9<br />incomeE: 32549<br />NAME: Marion County, Oregon<br />popE: 335553","Value: 42.9<br />incomeE: 40109<br />NAME: Multnomah County, Oregon<br />popE: 798647","Value: 43.0<br />incomeE: 45179<br />NAME: Washington County, Oregon<br />popE: 581821","Value: 44.1<br />incomeE: 36140<br />NAME: Yamhill County, Oregon<br />popE: 103820","Value: 27.5<br />incomeE: 39267<br />NAME: Adams County, Pennsylvania<br />popE: 102023","Value: 25.0<br />incomeE: 42344<br />NAME: Allegheny County, Pennsylvania<br />popE: 1225561","Value: 22.9<br />incomeE: 39826<br />NAME: Beaver County, Pennsylvania<br />popE: 166896","Value: 26.1<br />incomeE: 40310<br />NAME: Berks County, Pennsylvania<br />popE: 416642","Value: 24.0<br />incomeE: 33784<br />NAME: Blair County, Pennsylvania<br />popE: 123842","Value: 27.9<br />incomeE: 51417<br />NAME: Bucks County, Pennsylvania<br />popE: 626370","Value: 21.4<br />incomeE: 45016<br />NAME: Butler County, Pennsylvania<br />popE: 186566","Value: 21.6<br />incomeE: 33474<br />NAME: Cambria County, Pennsylvania<br />popE: 134550","Value: 21.8<br />incomeE: 39859<br />NAME: Centre County, Pennsylvania<br />popE: 161443","Value: 29.0<br />incomeE: 55456<br />NAME: Chester County, Pennsylvania<br />popE: 517156","Value: 27.4<br />incomeE: 43461<br />NAME: Cumberland County, Pennsylvania<br />popE: 247433","Value: 26.2<br />incomeE: 40170<br />NAME: Dauphin County, Pennsylvania<br />popE: 274515","Value: 31.1<br />incomeE: 46371<br />NAME: Delaware County, Pennsylvania<br />popE: 563527","Value: 22.4<br />incomeE: 35100<br />NAME: Erie County, Pennsylvania<br />popE: 275972","Value: 24.0<br />incomeE: 34829<br />NAME: Fayette County, Pennsylvania<br />popE: 132289","Value: 27.9<br />incomeE: 37968<br />NAME: Franklin County, Pennsylvania<br />popE: 153751","Value: 21.7<br />incomeE: 36760<br />NAME: Lackawanna County, Pennsylvania<br />popE: 211454","Value: 27.8<br />incomeE: 39843<br />NAME: Lancaster County, Pennsylvania<br />popE: 538347","Value: 26.3<br />incomeE: 36824<br />NAME: Lebanon County, Pennsylvania<br />popE: 138674","Value: 26.7<br />incomeE: 40659<br />NAME: Lehigh County, Pennsylvania<br />popE: 362613","Value: 21.6<br />incomeE: 35841<br />NAME: Luzerne County, Pennsylvania<br />popE: 317884","Value: 21.7<br />incomeE: 35013<br />NAME: Lycoming County, Pennsylvania<br />popE: 114859","Value: 22.1<br />incomeE: 33686<br />NAME: Mercer County, Pennsylvania<br />popE: 112630","Value: 22.5<br />incomeE: 38567<br />NAME: Monroe County, Pennsylvania<br />popE: 167586","Value: 28.6<br />incomeE: 53315<br />NAME: Montgomery County, Pennsylvania<br />popE: 821301","Value: 25.8<br />incomeE: 41590<br />NAME: Northampton County, Pennsylvania<br />popE: 301778","Value: 31.8<br />incomeE: 36467<br />NAME: Philadelphia County, Pennsylvania<br />popE: 1575522","Value: 23.0<br />incomeE: 36430<br />NAME: Schuylkill County, Pennsylvania<br />popE: 143555","Value: 24.8<br />incomeE: 40891<br />NAME: Washington County, Pennsylvania<br />popE: 207547","Value: 24.1<br />incomeE: 40484<br />NAME: Westmoreland County, Pennsylvania<br />popE: 354751","Value: 27.7<br />incomeE: 40860<br />NAME: York County, Pennsylvania<br />popE: 444014","Value: 27.5<br />incomeE: 46012<br />NAME: Kent County, Rhode Island<br />popE: 163861","Value: 26.8<br />incomeE: 40535<br />NAME: Providence County, Rhode Island<br />popE: 634533","Value: 28.2<br />incomeE: 50155<br />NAME: Washington County, Rhode Island<br />popE: 126242","Value: 42.3<br />incomeE: 35025<br />NAME: Aiken County, South Carolina<br />popE: 166926","Value: 39.0<br />incomeE: 34812<br />NAME: Anderson County, South Carolina<br />popE: 195995","Value: 45.3<br />incomeE: 33900<br />NAME: Beaufort County, South Carolina<br />popE: 182658","Value: 43.0<br />incomeE: 37644<br />NAME: Berkeley County, South Carolina<br />popE: 209065","Value: 44.3<br />incomeE: 40913<br />NAME: Charleston County, South Carolina<br />popE: 394708","Value: 43.9<br />incomeE: 40158<br />NAME: Dorchester County, South Carolina<br />popE: 155474","Value: 40.9<br />incomeE: 31971<br />NAME: Florence County, South Carolina<br />popE: 138561","Value: 37.5<br />incomeE: 37306<br />NAME: Greenville County, South Carolina<br />popE: 498402","Value: 40.9<br />incomeE: 29624<br />NAME: Horry County, South Carolina<br />popE: 320915","Value: 41.4<br />incomeE: 38853<br />NAME: Lexington County, South Carolina<br />popE: 286316","Value: 37.8<br />incomeE: 34159<br />NAME: Pickens County, South Carolina<br />popE: 122746","Value: 41.2<br />incomeE: 36374<br />NAME: Richland County, South Carolina<br />popE: 408263","Value: 37.6<br />incomeE: 33488<br />NAME: Spartanburg County, South Carolina<br />popE: 302195","Value: 40.4<br />incomeE: 30817<br />NAME: Sumter County, South Carolina<br />popE: 106995","Value: 36.8<br />incomeE: 40506<br />NAME: York County, South Carolina<br />popE: 258641","Value: 15.8<br />incomeE: 38132<br />NAME: Minnehaha County, South Dakota<br />popE: 186749","Value: 23.3<br />incomeE: 33433<br />NAME: Pennington County, South Dakota<br />popE: 109294","Value: 32.7<br />incomeE: 34613<br />NAME: Blount County, Tennessee<br />popE: 128443","Value: 34.8<br />incomeE: 34055<br />NAME: Bradley County, Tennessee<br />popE: 104557","Value: 33.9<br />incomeE: 37562<br />NAME: Davidson County, Tennessee<br />popE: 684017","Value: 34.8<br />incomeE: 36742<br />NAME: Hamilton County, Tennessee<br />popE: 357546","Value: 32.6<br />incomeE: 37349<br />NAME: Knox County, Tennessee<br />popE: 456185","Value: 33.3<br />incomeE: 36715<br />NAME: Montgomery County, Tennessee<br />popE: 196387","Value: 33.7<br />incomeE: 40292<br />NAME: Rutherford County, Tennessee<br />popE: 307128","Value: 35.4<br />incomeE: 35484<br />NAME: Shelby County, Tennessee<br />popE: 937005","Value: 31.8<br />incomeE: 31445<br />NAME: Sullivan County, Tennessee<br />popE: 156734","Value: 32.4<br />incomeE: 39822<br />NAME: Sumner County, Tennessee<br />popE: 179473","Value: 32.0<br />incomeE: 34163<br />NAME: Washington County, Tennessee<br />popE: 127055","Value: 33.5<br />incomeE: 59393<br />NAME: Williamson County, Tennessee<br />popE: 218648","Value: 33.3<br />incomeE: 42043<br />NAME: Wilson County, Tennessee<br />popE: 132663","Value: 44.6<br />incomeE: 35040<br />NAME: Bell County, Texas<br />popE: 342236","Value: 47.9<br />incomeE: 35006<br />NAME: Bexar County, Texas<br />popE: 1925865","Value: 49.3<br />incomeE: 50819<br />NAME: Brazoria County, Texas<br />popE: 353999","Value: 46.1<br />incomeE: 36434<br />NAME: Brazos County, Texas<br />popE: 219193","Value: 56.7<br />incomeE: 25296<br />NAME: Cameron County, Texas<br />popE: 421750","Value: 41.4<br />incomeE: 55869<br />NAME: Collin County, Texas<br />popE: 944350","Value: 46.4<br />incomeE: 42837<br />NAME: Comal County, Texas<br />popE: 135097","Value: 43.4<br />incomeE: 36727<br />NAME: Dallas County, Texas<br />popE: 2586552","Value: 42.0<br />incomeE: 50327<br />NAME: Denton County, Texas<br />popE: 807047","Value: 44.3<br />incomeE: 40711<br />NAME: Ector County, Texas<br />popE: 158342","Value: 43.0<br />incomeE: 42516<br />NAME: Ellis County, Texas<br />popE: 168838","Value: 44.7<br />incomeE: 29741<br />NAME: El Paso County, Texas<br />popE: 837654","Value: 48.5<br />incomeE: 53367<br />NAME: Fort Bend County, Texas<br />popE: 739342","Value: 49.1<br />incomeE: 45465<br />NAME: Galveston County, Texas<br />popE: 327089","Value: 40.4<br />incomeE: 35035<br />NAME: Grayson County, Texas<br />popE: 128560","Value: 41.8<br />incomeE: 32259<br />NAME: Gregg County, Texas<br />popE: 123494","Value: 47.2<br />incomeE: 41585<br />NAME: Guadalupe County, Texas<br />popE: 155137","Value: 48.2<br />incomeE: 39299<br />NAME: Harris County, Texas<br />popE: 4602523","Value: 45.9<br />incomeE: 41206<br />NAME: Hays County, Texas<br />popE: 204150","Value: 54.7<br />incomeE: 25670<br />NAME: Hidalgo County, Texas<br />popE: 849389","Value: 47.5<br />incomeE: 37310<br />NAME: Jefferson County, Texas<br />popE: 255210","Value: 42.1<br />incomeE: 41002<br />NAME: Johnson County, Texas<br />popE: 163475","Value: 42.3<br />incomeE: 40838<br />NAME: Kaufman County, Texas<br />popE: 118910","Value: 38.7<br />incomeE: 35288<br />NAME: Lubbock County, Texas<br />popE: 301454","Value: 43.9<br />incomeE: 32681<br />NAME: McLennan County, Texas<br />popE: 248429","Value: 44.0<br />incomeE: 49514<br />NAME: Midland County, Texas<br />popE: 164194","Value: 46.8<br />incomeE: 48141<br />NAME: Montgomery County, Texas<br />popE: 554445","Value: 53.7<br />incomeE: 35753<br />NAME: Nueces County, Texas<br />popE: 360486","Value: 42.1<br />incomeE: 43595<br />NAME: Parker County, Texas<br />popE: 129802","Value: 38.2<br />incomeE: 30896<br />NAME: Potter County, Texas<br />popE: 120899","Value: 37.1<br />incomeE: 42879<br />NAME: Randall County, Texas<br />popE: 132475","Value: 42.3<br />incomeE: 35355<br />NAME: Smith County, Texas<br />popE: 225015","Value: 42.9<br />incomeE: 41084<br />NAME: Tarrant County, Texas<br />popE: 2019977","Value: 41.7<br />incomeE: 33079<br />NAME: Taylor County, Texas<br />popE: 136348","Value: 43.3<br />incomeE: 33785<br />NAME: Tom Green County, Texas<br />popE: 117466","Value: 46.5<br />incomeE: 43878<br />NAME: Travis County, Texas<br />popE: 1203166","Value: 51.4<br />incomeE: 27948<br />NAME: Webb County, Texas<br />popE: 272053","Value: 40.9<br />incomeE: 32583<br />NAME: Wichita County, Texas<br />popE: 131818","Value: 45.7<br />incomeE: 47186<br />NAME: Williamson County, Texas<br />popE: 527057","Value: 29.7<br />incomeE: 35042<br />NAME: Cache County, Utah<br />popE: 122336","Value: 34.9<br />incomeE: 43904<br />NAME: Davis County, Utah<br />popE: 340621","Value: 35.1<br />incomeE: 40040<br />NAME: Salt Lake County, Utah<br />popE: 1120805","Value: 32.0<br />incomeE: 39979<br />NAME: Utah County, Utah<br />popE: 590440","Value: 41.8<br />incomeE: 31913<br />NAME: Washington County, Utah<br />popE: 160537","Value: 31.6<br />incomeE: 37190<br />NAME: Weber County, Utah<br />popE: 247731","Value: 17.7<br />incomeE: 44765<br />NAME: Chittenden County, Vermont<br />popE: 162052","Value: 32.9<br />incomeE: 45865<br />NAME: Albemarle County, Virginia<br />popE: 106355","Value: 32.8<br />incomeE: 76895<br />NAME: Arlington County, Virginia<br />popE: 231803","Value: 33.7<br />incomeE: 46503<br />NAME: Chesterfield County, Virginia<br />popE: 339447","Value: 32.3<br />incomeE: 63997<br />NAME: Fairfax County, Virginia<br />popE: 1143529","Value: 33.8<br />incomeE: 51545<br />NAME: Hanover County, Virginia<br />popE: 104449","Value: 34.4<br />incomeE: 43428<br />NAME: Henrico County, Virginia<br />popE: 325642","Value: 31.0<br />incomeE: 71746<br />NAME: Loudoun County, Virginia<br />popE: 385143","Value: 32.1<br />incomeE: 52944<br />NAME: Prince William County, Virginia<br />popE: 456749","Value: 31.3<br />incomeE: 46588<br />NAME: Spotsylvania County, Virginia<br />popE: 131412","Value: 30.7<br />incomeE: 57312<br />NAME: Stafford County, Virginia<br />popE: 144012","Value: 33.4<br />incomeE: 62582<br />NAME: Alexandria city, Virginia<br />popE: 156505","Value: 36.3<br />incomeE: 44158<br />NAME: Chesapeake city, Virginia<br />popE: 237820","Value: 36.4<br />incomeE: 37262<br />NAME: Hampton city, Virginia<br />popE: 135583","Value: 36.2<br />incomeE: 35947<br />NAME: Newport News city, Virginia<br />popE: 180145","Value: 37.0<br />incomeE: 34482<br />NAME: Norfolk city, Virginia<br />popE: 245592","Value: 34.3<br />incomeE: 34440<br />NAME: Richmond city, Virginia<br />popE: 223787","Value: 36.5<br />incomeE: 42279<br />NAME: Virginia Beach city, Virginia<br />popE: 450135","Value: 37.8<br />incomeE: 41968<br />NAME: Benton County, Washington<br />popE: 194168","Value: 43.2<br />incomeE: 43100<br />NAME: Clark County, Washington<br />popE: 465384","Value: 42.0<br />incomeE: 36217<br />NAME: Cowlitz County, Washington<br />popE: 105112","Value: 39.3<br />incomeE: 54346<br />NAME: King County, Washington<br />popE: 2163257","Value: 43.5<br />incomeE: 43035<br />NAME: Kitsap County, Washington<br />popE: 262475","Value: 39.1<br />incomeE: 42955<br />NAME: Pierce County, Washington<br />popE: 859840","Value: 36.7<br />incomeE: 38704<br />NAME: Skagit County, Washington<br />popE: 123907","Value: 38.0<br />incomeE: 49108<br />NAME: Snohomish County, Washington<br />popE: 786620","Value: 34.0<br />incomeE: 36896<br />NAME: Spokane County, Washington<br />popE: 497875","Value: 42.2<br />incomeE: 44021<br />NAME: Thurston County, Washington<br />popE: 274684","Value: 34.6<br />incomeE: 38282<br />NAME: Whatcom County, Washington<br />popE: 216812","Value: 34.3<br />incomeE: 30790<br />NAME: Yakima County, Washington<br />popE: 249325","Value: 30.0<br />incomeE: 40062<br />NAME: Berkeley County, West Virginia<br />popE: 113495","Value: 29.5<br />incomeE: 34722<br />NAME: Kanawha County, West Virginia<br />popE: 185710","Value: 26.0<br />incomeE: 38805<br />NAME: Monongalia County, West Virginia<br />popE: 105252","Value: 19.5<br />incomeE: 40155<br />NAME: Brown County, Wisconsin<br />popE: 259786","Value: 19.3<br />incomeE: 46181<br />NAME: Dane County, Wisconsin<br />popE: 529843","Value: 14.0<br />incomeE: 38448<br />NAME: Eau Claire County, Wisconsin<br />popE: 102991","Value: 18.7<br />incomeE: 39457<br />NAME: Fond du Lac County, Wisconsin<br />popE: 102315","Value: 22.4<br />incomeE: 40031<br />NAME: Kenosha County, Wisconsin<br />popE: 168330","Value: 16.7<br />incomeE: 39583<br />NAME: La Crosse County, Wisconsin<br />popE: 117850","Value: 14.3<br />incomeE: 39282<br />NAME: Marathon County, Wisconsin<br />popE: 135264","Value: 22.7<br />incomeE: 37331<br />NAME: Milwaukee County, Wisconsin<br />popE: 954209","Value: 18.2<br />incomeE: 41618<br />NAME: Outagamie County, Wisconsin<br />popE: 184754","Value: 21.8<br />incomeE: 40753<br />NAME: Racine County, Wisconsin<br />popE: 195398","Value: 19.1<br />incomeE: 36655<br />NAME: Rock County, Wisconsin<br />popE: 161769","Value: 20.2<br />incomeE: 40266<br />NAME: Sheboygan County, Wisconsin<br />popE: 115205","Value: 20.2<br />incomeE: 38168<br />NAME: Walworth County, Wisconsin<br />popE: 103013","Value: 18.7<br />incomeE: 47597<br />NAME: Washington County, Wisconsin<br />popE: 134535","Value: 20.5<br />incomeE: 51945<br />NAME: Waukesha County, Wisconsin<br />popE: 398879","Value: 18.7<br />incomeE: 40245<br />NAME: Winnebago County, Wisconsin<br />popE: 169926"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,139,1)","opacity":1,"size":[6.05691268027156,9.4094588612281,6.66111719835148,7.14750350432278,6.17126847395331,9.54207786767412,15.007981743224,6.08930988991828,5.50416936908688,6.50894878042139,8.06528664237379,11.3573917994403,7.61556456798157,4.464091557501,6.174384863927,4.12224203784309,13.219642043906,5.65698624361098,7.82637215976815,10.3442917166381,7.3965269808708,8.14530045493234,7.93690002231996,5.77569792467373,17.280860603589,6.42393533957218,13.0041977346578,7.85432583208447,13.4652630404163,9.12662566258299,11.5105900116463,10.073199955082,6.84812047795007,7.56129415176151,5.98886554568938,8.44097086560009,8.75168334648957,4.97733453219562,9.23656924445723,4.25211127594925,5.7029443812711,4.82251313247786,7.3863662402037,6.92004718734399,5.07794554945898,7.30443136188122,10.4828708635869,5.58720804369978,5.45140595684402,10.4731411412477,5.4787824028187,4.65330141045871,6.6652265398237,11.7940356326205,11.2558449900921,6.36022138254404,6.68241024482348,5.66989930078173,4.77322945570904,6.36977881659454,4.43058604173369,5.74506550704779,6.43348657610217,4.26870835768286,8.68795059045963,4.69338622410932,6.57130370439051,5.70502707001467,6.53635440500711,22.6771653543307,4.29310751285122,11.3918722112848,9.25700042807613,4.64092848230507,5.07858960604145,10.2638446828512,4.61379738194724,7.58149685517766,6.03224715998857,4.4313885299992,7.17350139667006,6.19996358356223,5.54783304401609,7.15076162048172,6.38307886489436,5.30617817859557,10.1831381025603,7.37790125376368,8.11456091940492,4.81176457228862,4.80885676137115,6.46145545449497,7.6568902817192,5.83350803598992,5.6677224938227,8.9695543929692,4.62008191082802,5.20348462780745,11.4501613787632,5.55035407514713,5.9506591125136,7.20996570492742,6.26855472488305,6.15417263959224,4.49173857622422,5.28681009878416,5.58153072612928,6.69216689425121,8.88441110377824,6.01779699899458,4.15122051016564,4.92741120158627,9.59442246957173,9.13620511478144,6.10929198793145,5.89049461435785,5.19341390998165,7.68053943172139,4.51114632037721,10.5967914261032,5.89615005312359,5.12604202826248,4.9824736759942,5.11835857341874,6.99084062336213,6.41661044350885,8.67402793492935,8.61100214258511,6.89979514833593,5.40049530689746,8.26962401260229,5.74922807951523,5.25259306631311,7.03109199744663,5.22772961677163,4.70060390891918,4.47944751538907,7.42380895801526,4.99311750979667,5.67111574447954,6.45492383629096,9.48670133744075,10.8992345796073,5.94231169955934,4.1622161600263,5.77726868192579,6.9920450875715,7.01962418938183,7.64998077688324,11.8729282437358,11.2740222931348,4.65973945466835,5.63508325642702,4.12938793284319,9.76686874005481,6.58947125885553,5.14916458224877,9.43276153387612,10.6673354368643,8.84907356738842,5.83722074128296,13.9870550475431,10.2349169191961,9.136667047924,10.7214775958835,10.8730213327081,4.79638866755174,4.33144385654769,5.72666237278625,5.3202900409589,4.56001041838281,8.42011633720163,7.41058715346311,5.7988203602622,7.13116541580445,9.93019170978255,6.25715861168878,11.0975632789999,5.6329783857138,6.02952255688211,12.7344542102752,7.35711392136266,6.31687047039402,5.8100597292001,8.08183621429233,14.5395424233187,7.92901221827564,3.77952755905512,8.48603984777643,12.6744525935169,5.69522784200587,9.32437633318598,6.41526203202204,5.50991923344159,5.76234898013517,7.04418534003669,5.2806932691941,6.07687315016628,6.44871574624149,6.9185375355197,5.48234749195886,4.24302657582964,5.66173255217283,6.0826762398139,4.17660827871317,6.88942355968591,4.18554816270505,7.39967650744028,10.2011062816012,4.9249492010278,6.70626459959505,8.27223907939014,11.6924236780149,7.61330159336529,4.32783258790551,4.82120908652866,5.7797967519078,9.40858592062913,7.60256835781165,6.11029407257545,15.7076149346831,8.71933417324924,8.43306119854474,5.62832792401674,7.5570339816147,5.17210343712881,7.20283627248384,11.383883237562,8.69018675963538,9.10555696617493,5.70131287655257,10.7304536028012,7.42292899713866,10.0729784424458,5.08994234064382,8.10446732167489,10.8946952566237,9.81722440822544,9.01990324203814,9.63287660120802,9.08374756251548,7.78145961781642,5.48815039414752,9.39664834088853,4.41957231755449,10.1229590106101,6.60983809302018,5.45667179417078,5.15239249490378,5.61821473275591,7.57816778305705,13.4349716114265,6.33908030284288,5.20717570007084,7.45191331911905,11.3372985785072,4.76851844194187,16.9812699119413,10.4786633223212,13.1368782399086,14.1135869677766,6.56472936959898,6.79402326932892,8.81545386160723,4.57404000896927,8.18008018327177,4.92086460170243,16.1576828477094,5.8077412302056,8.88322984372221,7.72453372380719,4.57780362522349,6.75439533398478,5.72802225390997,13.6138999270942,4.20079869102246,6.12448637826965,11.5597525700707,5.82732225511347,5.13720335063519,7.05651387430645,6.43328958429267,5.76076639434461,4.21061222267536,7.79823272165773,5.89575482905254,7.56926676383237,8.12706078921738,6.62515228264908,9.21062860776652,5.22428406464711,4.73907725046867,6.02148434084452,6.2947139426655,11.9337671728865,6.71730661963614,6.3323994152591,5.50115565546755,6.09560855454147,5.50156048724976,5.29678923517755,5.43230581573695,6.74638273687947,11.9005490692872,5.06173899829077,6.04740449222641,4.25373097874585,8.18061079446323,5.33660343227934,6.4564085107969,4.27956000815865,12.7458893927606,6.37432271959289,5.69240582818667,12.8292673883911,5.91456144402902,10.8225144144467,6.78557140638453,6.01787485374028,7.57162035382277,8.58988491016286,6.79728189723791,6.09387737767178,4.33232722605832,9.26459881755296,5.86222134640328,4.98675401902037,8.14228178357323,9.32636850389433,6.43782981348943,6.74485519253656,4.82871013052028,5.21399493845576,5.3700870500139,7.28526667123617,5.02195301870286,10.6725301394069,9.92815710867644,8.39320371046668,6.14427441191321,4.52192825343759,6.59661887457921,8.10543423521783,5.03059107493798,7.828016772339,10.7559386420466,9.57231774031275,4.26663781738755,4.11421578799993,12.6355100106506,5.93220027014243,8.47448097325662,5.05738253809906,9.834419281378,6.23005822084821,5.32203082448035,5.84202543805811,9.16923378196562,6.98075313652393,7.26314646075743,9.46118503524333,7.27769294782213,5.27006871282943,5.70766793821425,6.56159923904159,9.30456651443397,5.41255555976343,8.05462835912523,7.67293791951181,4.78289777583356,4.70222955030323,5.94334279363323,10.8682095630639,7.52598892183407,13.9196713797763,5.51360120027391,6.51221574608772,7.99004591104669,8.67345824059458,5.8824884729975,9.88122544439627,5.12124502523718,5.93268592671062,6.36068051586041,6.17383178245309,6.53150815089776,8.30872995350904,5.7385649074055,5.41014209557757,9.04656490305056,7.69997659069884,7.37927635322437,5.02713185509921,8.41186259978313,7.52986618367415,4.45672053249236,7.10053655632819,6.232659551177,4.56619299781691,5.17724957774156,4.31678831061371,10.1576156574032,8.01311832184614,8.75938088601086,6.3659681660769,7.57543264352438,11.4159259062304,5.76085434894031,6.12701168955874,5.14219995676644,6.65030826059357,5.27878826528149,7.88514621781829,15.0597419010951,7.98381661946626,6.65691720155941,8.51224787379212,11.4493752890548,5.33434106962668,16.9437417871282,10.7977776998988,5.78894084757554,5.96341566152407,10.94816070795,10.4530908054259,7.75448420517505,5.18016396675911,5.04785557175008,5.73256024936972,21.4944969501871,6.46854155306395,11.0049888876445,7.06433231985379,5.87608149572641,4.9149250408423,7.52297360077,6.99157854692107,5.88800009330298,9.40519812434757,8.03725276754238,5.21073549977655,4.97442128979204,5.27441153214237,6.726592991522,15.3468664363512,5.36213497158593,4.86969872635332,12.5469318423828,7.23842717021389,5.25901456316167,9.23288286310996,5.01562519241353,7.87141352022487,12.2131738782769,9.62394429275914,5.82665838426302,6.98399589856893,5.85229091996561,4.42293956820266,6.8058047055433,7.86140174230498,12.3065651779941,4.30973596774337,7.74177653600977,8.23451850905344,8.7633265994174,5.24941922026447,5.52276209764811,5.75682201462924,6.87432470656716,5.34519730903529,6.1369676151778,6.96064654097268,6.71203445804854,8.71685708729615,6.33589201626801,8.82335121086777,4.35165996099162,15.7708029572004,7.14053193088874,11.0552254745988,5.05915413880979,10.6955934567532,9.04307652887236,7.26483684608841,6.62793117186332,7.00128598921576,4.73434373926854,6.21785339814788,4.36012570696388,7.11253118661566,9.25065931400775,4.203191124402,4.14335460680044,5.95529340513907,4.88190678593796,5.33808003372375,11.4940455276103,6.2041501593039,6.35260676480094,5.84752692723674,4.79484513560724,4.20499710012162,5.3216918649172,8.34071321634175,5.98071052979907],"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,139,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[6.3,7.05949367088608,7.81898734177215,8.57848101265823,9.3379746835443,10.0974683544304,10.8569620253165,11.6164556962025,12.3759493670886,13.1354430379747,13.8949367088608,14.6544303797468,15.4139240506329,16.173417721519,16.9329113924051,17.6924050632911,18.4518987341772,19.2113924050633,19.9708860759494,20.7303797468354,21.4898734177215,22.2493670886076,23.0088607594937,23.7683544303797,24.5278481012658,25.2873417721519,26.046835443038,26.8063291139241,27.5658227848101,28.3253164556962,29.0848101265823,29.8443037974684,30.6037974683544,31.3632911392405,32.1227848101266,32.8822784810127,33.6417721518987,34.4012658227848,35.1607594936709,35.920253164557,36.679746835443,37.4392405063291,38.1987341772152,38.9582278481013,39.7177215189873,40.4772151898734,41.2367088607595,41.9962025316456,42.7556962025316,43.5151898734177,44.2746835443038,45.0341772151899,45.793670886076,46.553164556962,47.3126582278481,48.0721518987342,48.8316455696202,49.5911392405063,50.3506329113924,51.1101265822785,51.8696202531646,52.6291139240506,53.3886075949367,54.1481012658228,54.9075949367089,55.6670886075949,56.426582278481,57.1860759493671,57.9455696202532,58.7050632911392,59.4645569620253,60.2240506329114,60.9835443037975,61.7430379746835,62.5025316455696,63.2620253164557,64.0215189873418,64.7810126582279,65.5405063291139,66.3],"y":[45562.4677036128,45409.4283884305,45256.3890732482,45103.3497580659,44950.3104428836,44797.2711277013,44644.231812519,44491.1924973366,44338.1531821543,44185.113866972,44032.0745517897,43879.0352366074,43725.9959214251,43572.9566062428,43419.9172910605,43266.8779758782,43113.8386606958,42960.7993455135,42807.7600303312,42654.7207151489,42501.6813999666,42348.6420847843,42195.602769602,42042.5634544197,41889.5241392374,41736.484824055,41583.4455088727,41430.4061936904,41277.3668785081,41124.3275633258,40971.2882481435,40818.2489329612,40665.2096177789,40512.1703025965,40359.1309874142,40206.0916722319,40053.0523570496,39900.0130418673,39746.973726685,39593.9344115027,39440.8950963204,39287.8557811381,39134.8164659557,38981.7771507734,38828.7378355911,38675.6985204088,38522.6592052265,38369.6198900442,38216.5805748619,38063.5412596796,37910.5019444972,37757.4626293149,37604.4233141326,37451.3839989503,37298.344683768,37145.3053685857,36992.2660534034,36839.2267382211,36686.1874230388,36533.1481078564,36380.1087926741,36227.0694774918,36074.0301623095,35920.9908471272,35767.9515319449,35614.9122167626,35461.8729015803,35308.833586398,35155.7942712156,35002.7549560333,34849.715640851,34696.6763256687,34543.6370104864,34390.5976953041,34237.5583801218,34084.5190649395,33931.4797497571,33778.4404345748,33625.4011193925,33472.3618042102],"text":["Value: 6.300000<br />incomeE: 45562.47<br />popE: 1","Value: 7.059494<br />incomeE: 45409.43<br />popE: 1","Value: 7.818987<br />incomeE: 45256.39<br />popE: 1","Value: 8.578481<br />incomeE: 45103.35<br />popE: 1","Value: 9.337975<br />incomeE: 44950.31<br />popE: 1","Value: 10.097468<br />incomeE: 44797.27<br />popE: 1","Value: 10.856962<br />incomeE: 44644.23<br />popE: 1","Value: 11.616456<br />incomeE: 44491.19<br />popE: 1","Value: 12.375949<br />incomeE: 44338.15<br />popE: 1","Value: 13.135443<br />incomeE: 44185.11<br />popE: 1","Value: 13.894937<br />incomeE: 44032.07<br />popE: 1","Value: 14.654430<br />incomeE: 43879.04<br />popE: 1","Value: 15.413924<br />incomeE: 43726.00<br />popE: 1","Value: 16.173418<br />incomeE: 43572.96<br />popE: 1","Value: 16.932911<br />incomeE: 43419.92<br />popE: 1","Value: 17.692405<br />incomeE: 43266.88<br />popE: 1","Value: 18.451899<br />incomeE: 43113.84<br />popE: 1","Value: 19.211392<br />incomeE: 42960.80<br />popE: 1","Value: 19.970886<br />incomeE: 42807.76<br />popE: 1","Value: 20.730380<br />incomeE: 42654.72<br />popE: 1","Value: 21.489873<br />incomeE: 42501.68<br />popE: 1","Value: 22.249367<br />incomeE: 42348.64<br />popE: 1","Value: 23.008861<br />incomeE: 42195.60<br />popE: 1","Value: 23.768354<br />incomeE: 42042.56<br />popE: 1","Value: 24.527848<br />incomeE: 41889.52<br />popE: 1","Value: 25.287342<br />incomeE: 41736.48<br />popE: 1","Value: 26.046835<br />incomeE: 41583.45<br />popE: 1","Value: 26.806329<br />incomeE: 41430.41<br />popE: 1","Value: 27.565823<br />incomeE: 41277.37<br />popE: 1","Value: 28.325316<br />incomeE: 41124.33<br />popE: 1","Value: 29.084810<br />incomeE: 40971.29<br />popE: 1","Value: 29.844304<br />incomeE: 40818.25<br />popE: 1","Value: 30.603797<br />incomeE: 40665.21<br />popE: 1","Value: 31.363291<br />incomeE: 40512.17<br />popE: 1","Value: 32.122785<br />incomeE: 40359.13<br />popE: 1","Value: 32.882278<br />incomeE: 40206.09<br />popE: 1","Value: 33.641772<br />incomeE: 40053.05<br />popE: 1","Value: 34.401266<br />incomeE: 39900.01<br />popE: 1","Value: 35.160759<br />incomeE: 39746.97<br />popE: 1","Value: 35.920253<br />incomeE: 39593.93<br />popE: 1","Value: 36.679747<br />incomeE: 39440.90<br />popE: 1","Value: 37.439241<br />incomeE: 39287.86<br />popE: 1","Value: 38.198734<br />incomeE: 39134.82<br />popE: 1","Value: 38.958228<br />incomeE: 38981.78<br />popE: 1","Value: 39.717722<br />incomeE: 38828.74<br />popE: 1","Value: 40.477215<br />incomeE: 38675.70<br />popE: 1","Value: 41.236709<br />incomeE: 38522.66<br />popE: 1","Value: 41.996203<br />incomeE: 38369.62<br />popE: 1","Value: 42.755696<br />incomeE: 38216.58<br />popE: 1","Value: 43.515190<br />incomeE: 38063.54<br />popE: 1","Value: 44.274684<br />incomeE: 37910.50<br />popE: 1","Value: 45.034177<br />incomeE: 37757.46<br />popE: 1","Value: 45.793671<br />incomeE: 37604.42<br />popE: 1","Value: 46.553165<br />incomeE: 37451.38<br />popE: 1","Value: 47.312658<br />incomeE: 37298.34<br />popE: 1","Value: 48.072152<br />incomeE: 37145.31<br />popE: 1","Value: 48.831646<br />incomeE: 36992.27<br />popE: 1","Value: 49.591139<br />incomeE: 36839.23<br />popE: 1","Value: 50.350633<br />incomeE: 36686.19<br />popE: 1","Value: 51.110127<br />incomeE: 36533.15<br />popE: 1","Value: 51.869620<br />incomeE: 36380.11<br />popE: 1","Value: 52.629114<br />incomeE: 36227.07<br />popE: 1","Value: 53.388608<br />incomeE: 36074.03<br />popE: 1","Value: 54.148101<br />incomeE: 35920.99<br />popE: 1","Value: 54.907595<br />incomeE: 35767.95<br />popE: 1","Value: 55.667089<br />incomeE: 35614.91<br />popE: 1","Value: 56.426582<br />incomeE: 35461.87<br />popE: 1","Value: 57.186076<br />incomeE: 35308.83<br />popE: 1","Value: 57.945570<br />incomeE: 35155.79<br />popE: 1","Value: 58.705063<br />incomeE: 35002.75<br />popE: 1","Value: 59.464557<br />incomeE: 34849.72<br />popE: 1","Value: 60.224051<br />incomeE: 34696.68<br />popE: 1","Value: 60.983544<br />incomeE: 34543.64<br />popE: 1","Value: 61.743038<br />incomeE: 34390.60<br />popE: 1","Value: 62.502532<br />incomeE: 34237.56<br />popE: 1","Value: 63.262025<br />incomeE: 34084.52<br />popE: 1","Value: 64.021519<br />incomeE: 33931.48<br />popE: 1","Value: 64.781013<br />incomeE: 33778.44<br />popE: 1","Value: 65.540506<br />incomeE: 33625.40<br />popE: 1","Value: 66.300000<br />incomeE: 33472.36<br />popE: 1"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(255,140,0,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":57.7833125778331},"plot_bgcolor":"rgba(255,255,255,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[3.3,69.3],"tickmode":"array","ticktext":["20","40","60"],"tickvals":[20,40,60],"categoryorder":"array","categoryarray":["20","40","60"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":"<b> Average Temperature in January <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[21846.65,79516.35],"tickmode":"array","ticktext":["30000","40000","50000","60000","70000"],"tickvals":[30000,40000,50000,60000,70000],"categoryorder":"array","categoryarray":["30000","40000","50000","60000","70000"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(201,201,201,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":"<b> Median Household Earnings <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":1100,"height":500,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"37185e4498b":{"x":{},"y":{},"label":{},"size":{},"type":"scatter"},"371851333d0":{"x":{},"y":{},"label":{},"size":{}}},"cur_data":"37185e4498b","visdat":{"37185e4498b":["function (y) ","x"],"371851333d0":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> --- # Amenities and Income II <div id="htmlwidget-a68faa3351ccc6e4c80e" style="width:1100px;height:500px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-a68faa3351ccc6e4c80e">{"x":{"data":[{"x":[37540,36647,33007,33678,24968,36903,38774,49889,31563,33780,37237,35392,35355,32028,44347,42331,36404,57516,38422,35804,30076,40638,29453,37212,40052,41736,41623,38829,34781,31265,39589,35415,35275,39640,36173,36286,36213,29386,31997,39843,39198,27948,26939,36019,40648,33631,36824,35344,35824,36864,33644,39830,34694,41200,34027,40481,31978,32319,39306,40882,34985,35886,32980,37615,33516,36655,35856,31602,33474,32516,16048,39125,32083,35117,45941,35192,32366,41406,37714,34870,32617,36217,38779,38604,35083,34935,33481,28687,44739,47710,37165,39478,32764,33784,37179,41863,48822,47332,31346,42145,17075,33249,33014,41097,36696,36990,34395,43861,32123,50770,34410,41270,41073,34015,38282,35912,36881,36768,39071,44655,37968,33253,38610,30950,44947,34185,36684,36035,52929,48376,33018,43035,52380,25296,31917,33816,32192,35384,40987,41580,37968,32392,36294,37386,33107,35013,36534,35324,39282,32426,34294,32355,38638,40248,35281,46823,30790,40860,33174,33031,29665,39573,34394,40235,40110,41762,35936,41158,43721,40827,34264,43531,57265,35512,32119,33638,41585,35737,33487,40084,33038,36256,40246,38115,36717,33190,38342,41453,35438,40131,35486,33256,41918,31474,33981,35923,37838,38360,32885,36729,31462,46039,44472,41132,31798,37882,38338,38361,40694,38567,37159,28667,37043,29674,32517,35100,31855,36535,47278,36393,35636,42043,33071,32386,37295,35416,33774,31363,34062,39457,41291,31195,31287,31404,36344,33993,39267,36561,36358,30997,40003,35193,35653,37684,27145,34320,41674,40046,34462,35598,35704,33493,40333,35547,33242,41427,35016,50814,33151,31454,32587,33128,18194,43074,28318,29984,38162,31589,36068,30746,16322,25670,32946,34252,40275,49342,42023,47670,31705,35099,35970,32807,41735,35990,36174,31585,38704,34130,32965,29877,44039,31915,40087,31956,47534,37297,48009,33999,34278,45278,33892,40245,36287,28959,40032,40711,40745,37176,44021,41974,41777,35363,32423,32424,35194,39638,46260,41143,42148,32166,39482,32015,41387,38137,31949,16743,30501,43640,39824,34246,28959,40753,43914,34146,40310,34258,37970,42022,36251,37620,45214,40108,36298,31282,32021,42519,32882,36153,40119,33926,35957,42233,55525,16568,60983,20044,39458,31913,33893,41340,33305,31806,41730,41844,36281,37204,41245,36871,36173,50957,30186,24468,40266,35035,32444,30634,37064,39641,35921,32802,41683,41485,33665,33574,39859,36399,37171,30817,36779,41210],"y":[23.2,27.4,21.9,18.7,24.8,20.8,20.3,28,17.8,24.7,21.7,23.9,23.8,20.6,32.6,29.1,20.6,34.8,17,20.7,24,24.4,22.7,21.1,24.4,23.1,29.9,21.8,21.6,23.1,28.4,23.9,19.5,18.5,25.8,19.2,20.9,20.8,26.8,23.1,21.4,21.5,20.9,24.8,20.6,17.2,22.6,16.2,23.9,21.5,19.1,19.3,23.7,22.3,20.1,25,19.5,18.8,21.6,18.9,23.1,24.4,20.2,26.7,21.2,22.8,21.1,21.4,24.6,17.9,25.2,23.6,20.8,22.7,23.2,23.6,23.6,27.9,23,17.9,22.8,25.1,30.4,24,17.3,23.8,23.4,27.1,21.7,28.2,16.3,18,22.4,20.2,18.9,17.9,22,24,25,19.9,27.1,21.2,21.6,31.9,24.3,22.2,24,27.1,23.3,31,22.4,23.3,26.8,20.2,21.3,19,19.1,20.5,26.3,18.3,21.6,22.3,22.4,26.7,18.3,20.6,21.5,22,31.4,22.8,21.7,30.4,30.7,20.2,21.9,21.1,20.8,19.2,16.8,19.5,24.8,19.9,16.5,21.9,16.5,20.4,21.7,17.8,19.3,24.6,18.7,22.8,19.7,30.9,23.5,28.9,19,27.1,22.1,28.3,20,18.4,22.6,26.1,26.9,24.1,23.5,15.8,31.9,21.7,23.8,22.3,30.9,22.3,27.3,21,24.9,23.3,22,24.6,22,18.4,23.7,18,24,22.2,19.4,23.8,20.2,18.9,24.7,23.1,28.3,22.6,19.7,27.4,19.8,21.4,24.5,18.1,25.9,27.7,20.4,27,22.7,25.8,16.2,20.6,24.2,39.1,19.9,22,19.6,23.5,16.9,19.7,20.2,21,18.6,24.3,19.5,16.9,23.7,21.8,21.1,18.4,26.2,22.8,23.5,20.1,23.2,21.5,22.6,24,22.6,26.7,28.2,21.7,24.5,22,15.4,17.5,20.2,21.8,19.7,15.6,27.3,20,22.5,20.9,23.3,24.2,30.1,32,22.9,23.1,19.8,24.1,23.6,22.8,23.8,23.2,24.8,19.3,25.5,21.7,26.3,18.9,24.1,27.4,22.3,22.1,29.5,22.9,21.6,19.4,23,25.4,18.3,25,29,21.6,25,23.1,22.8,23.8,26.2,20.7,21.7,22.8,24.9,24.7,27.6,21.9,25.3,25.9,36.7,19.7,24.9,23.5,28.6,18.4,20,25.5,22.7,23.1,22.7,22.7,26.3,20.3,26.8,24.8,23.3,21.2,24.8,20.4,29.9,24.9,26.9,26.8,26.4,22,26.8,19.9,17.5,24.6,23.4,26,21.8,22,24.9,24.3,26.2,18.6,24.9,20.4,21.6,25.2,32.4,24.1,19.9,21.4,23.3,22.3,22.9,27.2,21.9,24.6,22.5,17.7,26.3,26,33.6,25.5,28.9,31.2,21.2,17.5,18.8,25.8,23.9,22.7,22.2,27,22.3,19.8,25.4,24.3,22.1,30.7,22.4,19.9,18,25.1,22,20.6,18,18.4,21.6,23,20.2,22.8,21.9,22.5,20.3,23.3,33.2,22.4,22.2,21.2],"text":["incomeE: 37540<br />commuteE: 23.2<br />NAME: Tallahassee, FL Metro Area<br />popE: 380101","incomeE: 36647<br />commuteE: 27.4<br />NAME: Tampa-St. Petersburg-Clearwater, FL Metro Area<br />popE: 3030047","incomeE: 33007<br />commuteE: 21.9<br />NAME: Terre Haute, IN Metro Area<br />popE: 170313","incomeE: 33678<br />commuteE: 18.7<br />NAME: Texarkana, TX-AR Metro Area<br />popE: 150034","incomeE: 24968<br />commuteE: 24.8<br />NAME: The Villages, FL Metro Area<br />popE: 120999","incomeE: 36903<br />commuteE: 20.8<br />NAME: Toledo, OH Metro Area<br />popE: 604620","incomeE: 38774<br />commuteE: 20.3<br />NAME: Topeka, KS Metro Area<br />popE: 233260","incomeE: 49889<br />commuteE: 28.0<br />NAME: Trenton, NJ Metro Area<br />popE: 368762","incomeE: 31563<br />commuteE: 17.8<br />NAME: Twin Falls, ID Metro Area<br />popE: 107097","incomeE: 33780<br />commuteE: 24.7<br />NAME: Tucson, AZ Metro Area<br />popE: 1019722","incomeE: 37237<br />commuteE: 21.7<br />NAME: Tulsa, OK Metro Area<br />popE: 985233","incomeE: 35392<br />commuteE: 23.9<br />NAME: Tuscaloosa, AL Metro Area<br />popE: 241398","incomeE: 35355<br />commuteE: 23.8<br />NAME: Tyler, TX Metro Area<br />popE: 225015","incomeE: 32028<br />commuteE: 20.6<br />NAME: Valdosta, GA Metro Area<br />popE: 144564","incomeE: 44347<br />commuteE: 32.6<br />NAME: Vallejo-Fairfield, CA Metro Area<br />popE: 438530","incomeE: 42331<br />commuteE: 29.1<br />NAME: Urban Honolulu, HI Metro Area<br />popE: 987638","incomeE: 36404<br />commuteE: 20.6<br />NAME: Utica-Rome, NY Metro Area<br />popE: 293287","incomeE: 57516<br />commuteE: 34.8<br />NAME: Washington-Arlington-Alexandria, DC-VA-MD-WV Metro Area<br />popE: 6138382","incomeE: 38422<br />commuteE: 17.0<br />NAME: Waterloo-Cedar Falls, IA Metro Area<br />popE: 170132","incomeE: 35804<br />commuteE: 20.7<br />NAME: Victoria, TX Metro Area<br />popE: 99501","incomeE: 30076<br />commuteE: 24.0<br />NAME: Vineland-Bridgeton, NJ Metro Area<br />popE: 153400","incomeE: 40638<br />commuteE: 24.4<br />NAME: Virginia Beach-Norfolk-Newport News, VA-NC Metro Area<br />popE: 1722001","incomeE: 29453<br />commuteE: 22.7<br />NAME: Visalia-Porterville, CA Metro Area<br />popE: 460477","incomeE: 37212<br />commuteE: 21.1<br />NAME: Kalamazoo-Portage, MI Metro Area<br />popE: 336845","incomeE: 40052<br />commuteE: 24.4<br />NAME: Kankakee, IL Metro Area<br />popE: 111061","incomeE: 41736<br />commuteE: 23.1<br />NAME: Kansas City, MO-KS Metro Area<br />popE: 2106632","incomeE: 41623<br />commuteE: 29.9<br />NAME: Houston-The Woodlands-Sugar Land, TX Metro Area<br />popE: 6779104","incomeE: 38829<br />commuteE: 21.8<br />NAME: Kennewick-Richland, WA Metro Area<br />popE: 284828","incomeE: 34781<br />commuteE: 21.6<br />NAME: Killeen-Temple, TX Metro Area<br />popE: 438265","incomeE: 31265<br />commuteE: 23.1<br />NAME: Kingsport-Bristol-Bristol, TN-VA Metro Area<br />popE: 306394","incomeE: 39589<br />commuteE: 28.4<br />NAME: Kingston, NY Metro Area<br />popE: 179303","incomeE: 35415<br />commuteE: 23.9<br />NAME: Knoxville, TN Metro Area<br />popE: 868499","incomeE: 35275<br />commuteE: 19.5<br />NAME: Kokomo, IN Metro Area<br />popE: 82387","incomeE: 39640<br />commuteE: 18.5<br />NAME: La Crosse-Onalaska, WI-MN Metro Area<br />popE: 136513","incomeE: 36173<br />commuteE: 25.8<br />NAME: Lafayette, LA Metro Area<br />popE: 488969","incomeE: 36286<br />commuteE: 19.2<br />NAME: Lafayette-West Lafayette, IN Metro Area<br />popE: 217955","incomeE: 36213<br />commuteE: 20.9<br />NAME: Lake Charles, LA Metro Area<br />popE: 207050","incomeE: 29386<br />commuteE: 20.8<br />NAME: Lake Havasu City-Kingman, AZ Metro Area<br />popE: 206064","incomeE: 31997<br />commuteE: 26.8<br />NAME: Lakeland-Winter Haven, FL Metro Area<br />popE: 668671","incomeE: 39843<br />commuteE: 23.1<br />NAME: Lancaster, PA Metro Area<br />popE: 538347","incomeE: 39198<br />commuteE: 21.4<br />NAME: Lansing-East Lansing, MI Metro Area<br />popE: 476615","incomeE: 27948<br />commuteE: 21.5<br />NAME: Laredo, TX Metro Area<br />popE: 272053","incomeE: 26939<br />commuteE: 20.9<br />NAME: Las Cruces, NM Metro Area<br />popE: 215338","incomeE: 36019<br />commuteE: 24.8<br />NAME: Las Vegas-Henderson-Paradise, NV Metro Area<br />popE: 2141574","incomeE: 40648<br />commuteE: 20.6<br />NAME: Lawrence, KS Metro Area<br />popE: 119319","incomeE: 33631<br />commuteE: 17.2<br />NAME: Lawton, OK Metro Area<br />popE: 128490","incomeE: 36824<br />commuteE: 22.6<br />NAME: Lebanon, PA Metro Area<br />popE: 138674","incomeE: 35344<br />commuteE: 16.2<br />NAME: Lewiston, ID-WA Metro Area<br />popE: 62492","incomeE: 35824<br />commuteE: 23.9<br />NAME: Lewiston-Auburn, ME Metro Area<br />popE: 107444","incomeE: 36864<br />commuteE: 21.5<br />NAME: Lexington-Fayette, KY Metro Area<br />popE: 506786","incomeE: 33644<br />commuteE: 19.1<br />NAME: Lima, OH Metro Area<br />popE: 103642","incomeE: 39830<br />commuteE: 19.3<br />NAME: Lincoln, NE Metro Area<br />popE: 327221","incomeE: 34694<br />commuteE: 23.7<br />NAME: Huntington-Ashland, WV-KY-OH Metro Area<br />popE: 358234","incomeE: 41200<br />commuteE: 22.3<br />NAME: Huntsville, AL Metro Area<br />popE: 450612","incomeE: 34027<br />commuteE: 20.1<br />NAME: Idaho Falls, ID Metro Area<br />popE: 142968","incomeE: 40481<br />commuteE: 25.0<br />NAME: Indianapolis-Carmel-Anderson, IN Metro Area<br />popE: 2007497","incomeE: 31978<br />commuteE: 19.5<br />NAME: Jonesboro, AR Metro Area<br />popE: 129755","incomeE: 32319<br />commuteE: 18.8<br />NAME: Joplin, MO Metro Area<br />popE: 177440","incomeE: 39306<br />commuteE: 21.6<br />NAME: Kahului-Wailuku-Lahaina, HI Metro Area<br />popE: 165356","incomeE: 40882<br />commuteE: 18.9<br />NAME: Ithaca, NY Metro Area<br />popE: 102962","incomeE: 34985<br />commuteE: 23.1<br />NAME: Jackson, MI Metro Area<br />popE: 158913","incomeE: 35886<br />commuteE: 24.4<br />NAME: Jackson, MS Metro Area<br />popE: 580280","incomeE: 32980<br />commuteE: 20.2<br />NAME: Jackson, TN Metro Area<br />popE: 129331","incomeE: 37615<br />commuteE: 26.7<br />NAME: Jacksonville, FL Metro Area<br />popE: 1475386","incomeE: 33516<br />commuteE: 21.2<br />NAME: Jacksonville, NC Metro Area<br />popE: 193912","incomeE: 36655<br />commuteE: 22.8<br />NAME: Janesville-Beloit, WI Metro Area<br />popE: 161769","incomeE: 35856<br />commuteE: 21.1<br />NAME: Jefferson City, MO Metro Area<br />popE: 151157","incomeE: 31602<br />commuteE: 21.4<br />NAME: Johnson City, TN Metro Area<br />popE: 201226","incomeE: 33474<br />commuteE: 24.6<br />NAME: Johnstown, PA Metro Area<br />popE: 134550","incomeE: 32516<br />commuteE: 17.9<br />NAME: Abilene, TX Metro Area<br />popE: 170009","incomeE: 16048<br />commuteE: 25.2<br />NAME: Aguadilla-Isabela, PR Metro Area<br />popE: 307555","incomeE: 39125<br />commuteE: 23.6<br />NAME: Akron, OH Metro Area<br />popE: 704454","incomeE: 32083<br />commuteE: 20.8<br />NAME: Albany, GA Metro Area<br />popE: 153101","incomeE: 35117<br />commuteE: 22.7<br />NAME: Albany, OR Metro Area<br />popE: 122870","incomeE: 45941<br />commuteE: 23.2<br />NAME: Albany-Schenectady-Troy, NY Metro Area<br />popE: 880481","incomeE: 35192<br />commuteE: 23.6<br />NAME: Albuquerque, NM Metro Area<br />popE: 910012","incomeE: 32366<br />commuteE: 23.6<br />NAME: Alexandria, LA Metro Area<br />popE: 153894","incomeE: 41406<br />commuteE: 27.9<br />NAME: Allentown-Bethlehem-Easton, PA-NJ Metro Area<br />popE: 834615","incomeE: 37714<br />commuteE: 23.0<br />NAME: Little Rock-North Little Rock-Conway, AR Metro Area<br />popE: 734502","incomeE: 34870<br />commuteE: 17.9<br />NAME: Logan, UT-ID Metro Area<br />popE: 135615","incomeE: 32617<br />commuteE: 22.8<br />NAME: Longview, TX Metro Area<br />popE: 217858","incomeE: 36217<br />commuteE: 25.1<br />NAME: Longview, WA Metro Area<br />popE: 105112","incomeE: 38779<br />commuteE: 30.4<br />NAME: Los Angeles-Long Beach-Anaheim, CA Metro Area<br />popE: 13262234","incomeE: 38604<br />commuteE: 24.0<br />NAME: Louisville/Jefferson County, KY-IN Metro Area<br />popE: 1285270","incomeE: 35083<br />commuteE: 17.3<br />NAME: Lubbock, TX Metro Area<br />popE: 313123","incomeE: 34935<br />commuteE: 23.8<br />NAME: Lynchburg, VA Metro Area<br />popE: 260668","incomeE: 33481<br />commuteE: 23.4<br />NAME: Macon-Bibb County, GA Metro Area<br />popE: 229676","incomeE: 28687<br />commuteE: 27.1<br />NAME: Madera, CA Metro Area<br />popE: 155013","incomeE: 44739<br />commuteE: 21.7<br />NAME: Madison, WI Metro Area<br />popE: 647281","incomeE: 47710<br />commuteE: 28.2<br />NAME: Manchester-Nashua, NH Metro Area<br />popE: 411087","incomeE: 37165<br />commuteE: 16.3<br />NAME: Manhattan, KS Metro Area<br />popE: 98841","incomeE: 39478<br />commuteE: 18.0<br />NAME: Mankato-North Mankato, MN Metro Area<br />popE: 100105","incomeE: 32764<br />commuteE: 22.4<br />NAME: Mansfield, OH Metro Area<br />popE: 121324","incomeE: 33784<br />commuteE: 20.2<br />NAME: Altoona, PA Metro Area<br />popE: 123842","incomeE: 37179<br />commuteE: 18.9<br />NAME: Amarillo, TX Metro Area<br />popE: 263412","incomeE: 41863<br />commuteE: 17.9<br />NAME: Ames, IA Metro Area<br />popE: 96922","incomeE: 48822<br />commuteE: 22.0<br />NAME: Anchorage, AK Metro Area<br />popE: 399576","incomeE: 47332<br />commuteE: 24.0<br />NAME: Ann Arbor, MI Metro Area<br />popE: 365961","incomeE: 31346<br />commuteE: 25.0<br />NAME: Anniston-Oxford-Jacksonville, AL Metro Area<br />popE: 115098","incomeE: 42145<br />commuteE: 19.9<br />NAME: Appleton, WI Metro Area<br />popE: 234561","incomeE: 17075<br />commuteE: 27.1<br />NAME: Arecibo, PR Metro Area<br />popE: 183890","incomeE: 33249<br />commuteE: 21.2<br />NAME: Asheville, NC Metro Area<br />popE: 449937","incomeE: 33014<br />commuteE: 21.6<br />NAME: Athens-Clarke County, GA Metro Area<br />popE: 205303","incomeE: 41097<br />commuteE: 31.9<br />NAME: Atlanta-Sandy Springs-Roswell, GA Metro Area<br />popE: 5779463","incomeE: 36696<br />commuteE: 24.3<br />NAME: Atlantic City-Hammonton, NJ Metro Area<br />popE: 268539","incomeE: 36990<br />commuteE: 22.2<br />NAME: Auburn-Opelika, AL Metro Area<br />popE: 159287","incomeE: 34395<br />commuteE: 24.0<br />NAME: Augusta-Richmond County, GA-SC Metro Area<br />popE: 594300","incomeE: 43861<br />commuteE: 27.1<br />NAME: Austin-Round Rock, TX Metro Area<br />popE: 2058351","incomeE: 32123<br />commuteE: 23.3<br />NAME: Bakersfield, CA Metro Area<br />popE: 883053","incomeE: 50770<br />commuteE: 31.0<br />NAME: Baltimore-Columbia-Towson, MD Metro Area<br />popE: 2793250","incomeE: 34410<br />commuteE: 22.4<br />NAME: Bangor, ME Metro Area<br />popE: 151748","incomeE: 41270<br />commuteE: 23.3<br />NAME: Barnstable Town, MA Metro Area<br />popE: 213690","incomeE: 41073<br />commuteE: 26.8<br />NAME: Baton Rouge, LA Metro Area<br />popE: 829642","incomeE: 34015<br />commuteE: 20.2<br />NAME: Battle Creek, MI Metro Area<br />popE: 134473","incomeE: 38282<br />commuteE: 21.3<br />NAME: Bellingham, WA Metro Area<br />popE: 216812","incomeE: 35912<br />commuteE: 19.0<br />NAME: Bend-Redmond, OR Metro Area<br />popE: 180640","incomeE: 36881<br />commuteE: 19.1<br />NAME: Billings, MT Metro Area<br />popE: 169086","incomeE: 36768<br />commuteE: 20.5<br />NAME: Binghamton, NY Metro Area<br />popE: 243447","incomeE: 39071<br />commuteE: 26.3<br />NAME: Birmingham-Hoover, AL Metro Area<br />popE: 1147054","incomeE: 44655<br />commuteE: 18.3<br />NAME: Bismarck, ND Metro Area<br />popE: 130531","incomeE: 37968<br />commuteE: 21.6<br />NAME: Blacksburg-Christiansburg-Radford, VA Metro Area<br />popE: 182341","incomeE: 33253<br />commuteE: 22.3<br />NAME: Bay City, MI Metro Area<br />popE: 104786","incomeE: 38610<br />commuteE: 22.4<br />NAME: Beaumont-Port Arthur, TX Metro Area<br />popE: 409693","incomeE: 30950<br />commuteE: 26.7<br />NAME: Beckley, WV Metro Area<br />popE: 120358","incomeE: 44947<br />commuteE: 18.3<br />NAME: Bloomington, IL Metro Area<br />popE: 189261","incomeE: 34185<br />commuteE: 20.6<br />NAME: Bloomington, IN Metro Area<br />popE: 166281","incomeE: 36684<br />commuteE: 21.5<br />NAME: Bloomsburg-Berwick, PA Metro Area<br />popE: 84514","incomeE: 36035<br />commuteE: 22.0<br />NAME: Boise City, ID Metro Area<br />popE: 693952","incomeE: 52929<br />commuteE: 31.4<br />NAME: Boston-Cambridge-Newton, MA-NH Metro Area<br />popE: 4811732","incomeE: 48376<br />commuteE: 22.8<br />NAME: Boulder, CO Metro Area<br />popE: 321030","incomeE: 33018<br />commuteE: 21.7<br />NAME: Bowling Green, KY Metro Area<br />popE: 172088","incomeE: 43035<br />commuteE: 30.4<br />NAME: Bremerton-Silverdale, WA Metro Area<br />popE: 262475","incomeE: 52380<br />commuteE: 30.7<br />NAME: Bridgeport-Stamford-Norwalk, CT Metro Area<br />popE: 944348","incomeE: 25296<br />commuteE: 20.2<br />NAME: Brownsville-Harlingen, TX Metro Area<br />popE: 421750","incomeE: 31917<br />commuteE: 21.9<br />NAME: Brunswick, GA Metro Area<br />popE: 116655","incomeE: 33816<br />commuteE: 21.1<br />NAME: Cape Girardeau, MO-IL Metro Area<br />popE: 97137","incomeE: 32192<br />commuteE: 20.8<br />NAME: Carbondale-Marion, IL Metro Area<br />popE: 125850","incomeE: 35384<br />commuteE: 19.2<br />NAME: Carson City, NV Metro Area<br />popE: 54467","incomeE: 40987<br />commuteE: 16.8<br />NAME: Casper, WY Metro Area<br />popE: 80610","incomeE: 41580<br />commuteE: 19.5<br />NAME: Cedar Rapids, IA Metro Area<br />popE: 268315","incomeE: 37968<br />commuteE: 24.8<br />NAME: Chambersburg-Waynesboro, PA Metro Area<br />popE: 153751","incomeE: 32392<br />commuteE: 19.9<br />NAME: Waco, TX Metro Area<br />popE: 265728","incomeE: 36294<br />commuteE: 16.5<br />NAME: Walla Walla, WA Metro Area<br />popE: 64237","incomeE: 37386<br />commuteE: 21.9<br />NAME: Warner Robins, GA Metro Area<br />popE: 189943","incomeE: 33107<br />commuteE: 16.5<br />NAME: Wichita Falls, TX Metro Area<br />popE: 150994","incomeE: 35013<br />commuteE: 20.4<br />NAME: Williamsport, PA Metro Area<br />popE: 114859","incomeE: 36534<br />commuteE: 21.7<br />NAME: Wilmington, NC Metro Area<br />popE: 283251","incomeE: 35324<br />commuteE: 17.8<br />NAME: Watertown-Fort Drum, NY Metro Area<br />popE: 114448","incomeE: 39282<br />commuteE: 19.3<br />NAME: Wausau, WI Metro Area<br />popE: 135264","incomeE: 32426<br />commuteE: 24.6<br />NAME: Weirton-Steubenville, WV-OH Metro Area<br />popE: 119338","incomeE: 34294<br />commuteE: 18.7<br />NAME: Wenatchee, WA Metro Area<br />popE: 117128","incomeE: 32355<br />commuteE: 22.8<br />NAME: Wheeling, WV-OH Metro Area<br />popE: 142664","incomeE: 38638<br />commuteE: 19.7<br />NAME: Wichita, KS Metro Area<br />popE: 643765","incomeE: 40248<br />commuteE: 30.9<br />NAME: Winchester, VA-WV Metro Area<br />popE: 136305","incomeE: 35281<br />commuteE: 23.5<br />NAME: Winston-Salem, NC Metro Area<br />popE: 661798","incomeE: 46823<br />commuteE: 28.9<br />NAME: Worcester, MA-CT Metro Area<br />popE: 938818","incomeE: 30790<br />commuteE: 19.0<br />NAME: Yakima, WA Metro Area<br />popE: 249325","incomeE: 40860<br />commuteE: 27.1<br />NAME: York-Hanover, PA Metro Area<br />popE: 444014","incomeE: 33174<br />commuteE: 22.1<br />NAME: Youngstown-Warren-Boardman, OH-PA Metro Area<br />popE: 545488","incomeE: 33031<br />commuteE: 28.3<br />NAME: Yuba City, CA Metro Area<br />popE: 171365","incomeE: 29665<br />commuteE: 20.0<br />NAME: Yuma, AZ Metro Area<br />popE: 207829","incomeE: 39573<br />commuteE: 18.4<br />NAME: Champaign-Urbana, IL Metro Area<br />popE: 239273","incomeE: 34394<br />commuteE: 22.6<br />NAME: Charleston, WV Metro Area<br />popE: 217312","incomeE: 40235<br />commuteE: 26.1<br />NAME: Charleston-North Charleston, SC Metro Area<br />popE: 759247","incomeE: 40110<br />commuteE: 26.9<br />NAME: Charlotte-Concord-Gastonia, NC-SC Metro Area<br />popE: 2473125","incomeE: 41762<br />commuteE: 24.1<br />NAME: Charlottesville, VA Metro Area<br />popE: 230905","incomeE: 35936<br />commuteE: 23.5<br />NAME: Chattanooga, TN-GA Metro Area<br />popE: 552043","incomeE: 41158<br />commuteE: 15.8<br />NAME: Cheyenne, WY Metro Area<br />popE: 97692","incomeE: 43721<br />commuteE: 31.9<br />NAME: Chicago-Naperville-Elgin, IL-IN-WI Metro Area<br />popE: 9536428","incomeE: 40827<br />commuteE: 21.7<br />NAME: Buffalo-Cheektowaga-Niagara Falls, NY Metro Area<br />popE: 1131570","incomeE: 34264<br />commuteE: 23.8<br />NAME: Burlington, NC Metro Area<br />popE: 160576","incomeE: 43531<br />commuteE: 22.3<br />NAME: Burlington-South Burlington, VT Metro Area<br />popE: 218042","incomeE: 57265<br />commuteE: 30.9<br />NAME: California-Lexington Park, MD Metro Area<br />popE: 111531","incomeE: 35512<br />commuteE: 22.3<br />NAME: Canton-Massillon, OH Metro Area<br />popE: 401053","incomeE: 32119<br />commuteE: 27.3<br />NAME: Cape Coral-Fort Myers, FL Metro Area<br />popE: 718679","incomeE: 33638<br />commuteE: 21.0<br />NAME: Chico, CA Metro Area<br />popE: 227075","incomeE: 41585<br />commuteE: 24.9<br />NAME: Cincinnati, OH-KY-IN Metro Area<br />popE: 2168825","incomeE: 35737<br />commuteE: 23.3<br />NAME: Clarksville, TN-KY Metro Area<br />popE: 282994","incomeE: 33487<br />commuteE: 22.0<br />NAME: Cleveland, TN Metro Area<br />popE: 121339","incomeE: 40084<br />commuteE: 24.6<br />NAME: Cleveland-Elyria, OH Metro Area<br />popE: 2061766","incomeE: 33038<br />commuteE: 22.0<br />NAME: Coeur d'Alene, ID Metro Area<br />popE: 153605","incomeE: 36256<br />commuteE: 18.4<br />NAME: College Station-Bryan, TX Metro Area<br />popE: 253946","incomeE: 40246<br />commuteE: 23.7<br />NAME: Colorado Springs, CO Metro Area<br />popE: 712266","incomeE: 38115<br />commuteE: 18.0<br />NAME: Columbia, MO Metro Area<br />popE: 176515","incomeE: 36717<br />commuteE: 24.0<br />NAME: Columbia, SC Metro Area<br />popE: 816664","incomeE: 33190<br />commuteE: 22.2<br />NAME: Columbus, GA-AL Metro Area<br />popE: 307724","incomeE: 38342<br />commuteE: 19.4<br />NAME: Columbus, IN Metro Area<br />popE: 81893","incomeE: 41453<br />commuteE: 23.8<br />NAME: Columbus, OH Metro Area<br />popE: 2054062","incomeE: 35438<br />commuteE: 20.2<br />NAME: Corpus Christi, TX Metro Area<br />popE: 452295","incomeE: 40131<br />commuteE: 18.9<br />NAME: Corvallis, OR Metro Area<br />popE: 89780","incomeE: 35486<br />commuteE: 24.7<br />NAME: Crestview-Fort Walton Beach-Destin, FL Metro Area<br />popE: 266595","incomeE: 33256<br />commuteE: 23.1<br />NAME: Cumberland, MD-WV Metro Area<br />popE: 99255","incomeE: 41918<br />commuteE: 28.3<br />NAME: Dallas-Fort Worth-Arlington, TX Metro Area<br />popE: 7255028","incomeE: 31474<br />commuteE: 22.6<br />NAME: Dalton, GA Metro Area<br />popE: 143406","incomeE: 33981<br />commuteE: 19.7<br />NAME: Danville, IL Metro Area<br />popE: 78407","incomeE: 35923<br />commuteE: 27.4<br />NAME: Daphne-Fairhope-Foley, AL Metro Area<br />popE: 208107","incomeE: 37838<br />commuteE: 19.8<br />NAME: Davenport-Moline-Rock Island, IA-IL Metro Area<br />popE: 382720","incomeE: 38360<br />commuteE: 21.4<br />NAME: Dayton, OH Metro Area<br />popE: 802645","incomeE: 32885<br />commuteE: 24.5<br />NAME: Decatur, AL Metro Area<br />popE: 152293","incomeE: 36729<br />commuteE: 18.1<br />NAME: Decatur, IL Metro Area<br />popE: 106512","incomeE: 31462<br />commuteE: 25.9<br />NAME: Deltona-Daytona Beach-Ormond Beach, FL Metro Area<br />popE: 634773","incomeE: 46039<br />commuteE: 27.7<br />NAME: Denver-Aurora-Lakewood, CO Metro Area<br />popE: 2850221","incomeE: 44472<br />commuteE: 20.4<br />NAME: Des Moines-West Des Moines, IA Metro Area<br />popE: 634201","incomeE: 41132<br />commuteE: 27.0<br />NAME: Detroit-Warren-Dearborn, MI Metro Area<br />popE: 4317179","incomeE: 31798<br />commuteE: 22.7<br />NAME: Dothan, AL Metro Area<br />popE: 147967","incomeE: 37882<br />commuteE: 25.8<br />NAME: Dover, DE Metro Area<br />popE: 174822","incomeE: 38338<br />commuteE: 16.2<br />NAME: Dubuque, IA Metro Area<br />popE: 96802","incomeE: 38361<br />commuteE: 20.6<br />NAME: Duluth, MN-WI Metro Area<br />popE: 279022","incomeE: 40694<br />commuteE: 24.2<br />NAME: Durham-Chapel Hill, NC Metro Area<br />popE: 558491","incomeE: 38567<br />commuteE: 39.1<br />NAME: East Stroudsburg, PA Metro Area<br />popE: 167586","incomeE: 37159<br />commuteE: 19.9<br />NAME: Eau Claire, WI Metro Area<br />popE: 166626","incomeE: 28667<br />commuteE: 22.0<br />NAME: El Centro, CA Metro Area<br />popE: 180216","incomeE: 37043<br />commuteE: 19.6<br />NAME: Elmira, NY Metro Area<br />popE: 85740","incomeE: 29674<br />commuteE: 23.5<br />NAME: El Paso, TX Metro Area<br />popE: 841752","incomeE: 32517<br />commuteE: 16.9<br />NAME: Enid, OK Metro Area<br />popE: 62190","incomeE: 35100<br />commuteE: 19.7<br />NAME: Erie, PA Metro Area<br />popE: 275972","incomeE: 31855<br />commuteE: 20.2<br />NAME: Eugene, OR Metro Area<br />popE: 368882","incomeE: 36535<br />commuteE: 21.0<br />NAME: Evansville, IN-KY Metro Area<br />popE: 314967","incomeE: 47278<br />commuteE: 18.6<br />NAME: Fairbanks, AK Metro Area<br />popE: 99653","incomeE: 36393<br />commuteE: 24.3<br />NAME: Elizabethtown-Fort Knox, KY Metro Area<br />popE: 150577","incomeE: 35636<br />commuteE: 19.5<br />NAME: Elkhart-Goshen, IN Metro Area<br />popE: 203604","incomeE: 42043<br />commuteE: 16.9<br />NAME: Fargo, ND-MN Metro Area<br />popE: 237003","incomeE: 33071<br />commuteE: 23.7<br />NAME: Farmington, NM Metro Area<br />popE: 127455","incomeE: 32386<br />commuteE: 21.8<br />NAME: Fayetteville, NC Metro Area<br />popE: 385345","incomeE: 37295<br />commuteE: 21.1<br />NAME: Fayetteville-Springdale-Rogers, AR-MO Metro Area<br />popE: 526412","incomeE: 35416<br />commuteE: 18.4<br />NAME: Flagstaff, AZ Metro Area<br />popE: 140217","incomeE: 33774<br />commuteE: 26.2<br />NAME: Flint, MI Metro Area<br />popE: 409361","incomeE: 31363<br />commuteE: 22.8<br />NAME: Florence, SC Metro Area<br />popE: 205814","incomeE: 34062<br />commuteE: 23.5<br />NAME: Florence-Muscle Shoals, AL Metro Area<br />popE: 147080","incomeE: 39457<br />commuteE: 20.1<br />NAME: Fond du Lac, WI Metro Area<br />popE: 102315","incomeE: 41291<br />commuteE: 23.2<br />NAME: Fort Collins, CO Metro Area<br />popE: 338161","incomeE: 31195<br />commuteE: 21.5<br />NAME: Fort Smith, AR-OK Metro Area<br />popE: 281201","incomeE: 31287<br />commuteE: 22.6<br />NAME: Fresno, CA Metro Area<br />popE: 978130","incomeE: 31404<br />commuteE: 24.0<br />NAME: Gadsden, AL Metro Area<br />popE: 102939","incomeE: 36344<br />commuteE: 22.6<br />NAME: Gainesville, FL Metro Area<br />popE: 280763","incomeE: 33993<br />commuteE: 26.7<br />NAME: Gainesville, GA Metro Area<br />popE: 195961","incomeE: 39267<br />commuteE: 28.2<br />NAME: Gettysburg, PA Metro Area<br />popE: 102023","incomeE: 36561<br />commuteE: 21.7<br />NAME: Fort Wayne, IN Metro Area<br />popE: 431612","incomeE: 36358<br />commuteE: 24.5<br />NAME: Glens Falls, NY Metro Area<br />popE: 126308","incomeE: 30997<br />commuteE: 22.0<br />NAME: Goldsboro, NC Metro Area<br />popE: 124002","incomeE: 40003<br />commuteE: 15.4<br />NAME: Grand Forks, ND-MN Metro Area<br />popE: 101991","incomeE: 35193<br />commuteE: 17.5<br />NAME: Grand Island, NE Metro Area<br />popE: 84729","incomeE: 35653<br />commuteE: 20.2<br />NAME: Grand Junction, CO Metro Area<br />popE: 149998","incomeE: 37684<br />commuteE: 21.8<br />NAME: Grand Rapids-Wyoming, MI Metro Area<br />popE: 1050440","incomeE: 27145<br />commuteE: 19.7<br />NAME: Grants Pass, OR Metro Area<br />popE: 85481","incomeE: 34320<br />commuteE: 15.6<br />NAME: Great Falls, MT Metro Area<br />popE: 81746","incomeE: 41674<br />commuteE: 27.3<br />NAME: Greeley, CO Metro Area<br />popE: 295123","incomeE: 40046<br />commuteE: 20.0<br />NAME: Green Bay, WI Metro Area<br />popE: 317702","incomeE: 34462<br />commuteE: 22.5<br />NAME: Greensboro-High Point, NC Metro Area<br />popE: 757810","incomeE: 35598<br />commuteE: 20.9<br />NAME: Greenville, NC Metro Area<br />popE: 177372","incomeE: 35704<br />commuteE: 23.3<br />NAME: Greenville-Anderson-Mauldin, SC Metro Area<br />popE: 883853","incomeE: 33493<br />commuteE: 24.2<br />NAME: Gulfport-Biloxi-Pascagoula, MS Metro Area<br />popE: 391293","incomeE: 40333<br />commuteE: 30.1<br />NAME: Hagerstown-Martinsburg, MD-WV Metro Area<br />popE: 263306","incomeE: 35547<br />commuteE: 32.0<br />NAME: Hammond, LA Metro Area<br />popE: 130504","incomeE: 33242<br />commuteE: 22.9<br />NAME: Hanford-Corcoran, CA Metro Area<br />popE: 150075","incomeE: 41427<br />commuteE: 23.1<br />NAME: Harrisburg-Carlisle, PA Metro Area<br />popE: 567872","incomeE: 35016<br />commuteE: 19.8<br />NAME: Harrisonburg, VA Metro Area<br />popE: 132835","incomeE: 50814<br />commuteE: 24.1<br />NAME: Hartford-West Hartford-East Hartford, CT Metro Area<br />popE: 1209367","incomeE: 33151<br />commuteE: 23.6<br />NAME: Hattiesburg, MS Metro Area<br />popE: 148768","incomeE: 31454<br />commuteE: 22.8<br />NAME: Hickory-Lenoir-Morganton, NC Metro Area<br />popE: 365339","incomeE: 32587<br />commuteE: 23.8<br />NAME: Hilton Head Island-Bluffton-Beaufort, SC Metro Area<br />popE: 210558","incomeE: 33128<br />commuteE: 23.2<br />NAME: Hinesville, GA Metro Area<br />popE: 80264","incomeE: 18194<br />commuteE: 24.8<br />NAME: Guayama, PR Metro Area<br />popE: 77151","incomeE: 43074<br />commuteE: 19.3<br />NAME: Iowa City, IA Metro Area<br />popE: 169144","incomeE: 28318<br />commuteE: 25.5<br />NAME: Homosassa Springs, FL Metro Area<br />popE: 143087","incomeE: 29984<br />commuteE: 21.7<br />NAME: Hot Springs, AR Metro Area<br />popE: 98296","incomeE: 38162<br />commuteE: 26.3<br />NAME: Houma-Thibodaux, LA Metro Area<br />popE: 210801","incomeE: 31589<br />commuteE: 18.9<br />NAME: Medford, OR Metro Area<br />popE: 214267","incomeE: 36068<br />commuteE: 24.1<br />NAME: Memphis, TN-MS-AR Metro Area<br />popE: 1345991","incomeE: 30746<br />commuteE: 27.4<br />NAME: Merced, CA Metro Area<br />popE: 269075","incomeE: 16322<br />commuteE: 22.3<br />NAME: Mayagüez, PR Metro Area<br />popE: 93435","incomeE: 25670<br />commuteE: 22.1<br />NAME: McAllen-Edinburg-Mission, TX Metro Area<br />popE: 849389","incomeE: 32946<br />commuteE: 29.5<br />NAME: Miami-Fort Lauderdale-West Palm Beach, FL Metro Area<br />popE: 6070944","incomeE: 34252<br />commuteE: 22.9<br />NAME: Michigan City-La Porte, IN Metro Area<br />popE: 110552","incomeE: 40275<br />commuteE: 21.6<br />NAME: Midland, MI Metro Area<br />popE: 83389","incomeE: 49342<br />commuteE: 19.4<br />NAME: Midland, TX Metro Area<br />popE: 169808","incomeE: 42023<br />commuteE: 23.0<br />NAME: Milwaukee-Waukesha-West Allis, WI Metro Area<br />popE: 1575907","incomeE: 47670<br />commuteE: 25.4<br />NAME: Minneapolis-St. Paul-Bloomington, MN-WI Metro Area<br />popE: 3557528","incomeE: 31705<br />commuteE: 18.3<br />NAME: Missoula, MT Metro Area<br />popE: 115983","incomeE: 35099<br />commuteE: 25.0<br />NAME: Mobile, AL Metro Area<br />popE: 414659","incomeE: 35970<br />commuteE: 29.0<br />NAME: Modesto, CA Metro Area<br />popE: 539301","incomeE: 32807<br />commuteE: 21.6<br />NAME: Monroe, LA Metro Area<br />popE: 178550","incomeE: 41735<br />commuteE: 25.0<br />NAME: Monroe, MI Metro Area<br />popE: 149699","incomeE: 35990<br />commuteE: 23.1<br />NAME: Montgomery, AL Metro Area<br />popE: 373589","incomeE: 36174<br />commuteE: 22.8<br />NAME: Morgantown, WV Metro Area<br />popE: 139089","incomeE: 31585<br />commuteE: 23.8<br />NAME: Morristown, TN Metro Area<br />popE: 116987","incomeE: 38704<br />commuteE: 26.2<br />NAME: Mount Vernon-Anacortes, WA Metro Area<br />popE: 123907","incomeE: 34130<br />commuteE: 20.7<br />NAME: Muncie, IN Metro Area<br />popE: 115616","incomeE: 32965<br />commuteE: 21.7<br />NAME: Muskegon, MI Metro Area<br />popE: 173043","incomeE: 29877<br />commuteE: 22.8<br />NAME: Myrtle Beach-Conway-North Myrtle Beach, SC-NC Metro Area<br />popE: 447775","incomeE: 44039<br />commuteE: 24.9<br />NAME: Napa, CA Metro Area<br />popE: 140530","incomeE: 31915<br />commuteE: 24.7<br />NAME: Naples-Immokalee-Marco Island, FL Metro Area<br />popE: 363922","incomeE: 40087<br />commuteE: 27.6<br />NAME: Nashville-Davidson--Murfreesboro--Franklin, TN Metro Area<br />popE: 1864138","incomeE: 31956<br />commuteE: 21.9<br />NAME: New Bern, NC Metro Area<br />popE: 125519","incomeE: 47534<br />commuteE: 25.3<br />NAME: New Haven-Milford, CT Metro Area<br />popE: 859339","incomeE: 37297<br />commuteE: 25.9<br />NAME: New Orleans-Metairie, LA Metro Area<br />popE: 1263635","incomeE: 48009<br />commuteE: 36.7<br />NAME: New York-Newark-Jersey City, NY-NJ-PA Metro Area<br />popE: 19990592","incomeE: 33999<br />commuteE: 19.7<br />NAME: Niles-Benton Harbor, MI Metro Area<br />popE: 154807","incomeE: 34278<br />commuteE: 24.9<br />NAME: North Port-Sarasota-Bradenton, FL Metro Area<br />popE: 785997","incomeE: 45278<br />commuteE: 23.5<br />NAME: Norwich-New London, CT Metro Area<br />popE: 268881","incomeE: 33892<br />commuteE: 28.6<br />NAME: Orlando-Kissimmee-Sanford, FL Metro Area<br />popE: 2450261","incomeE: 40245<br />commuteE: 18.4<br />NAME: Oshkosh-Neenah, WI Metro Area<br />popE: 169926","incomeE: 36287<br />commuteE: 20.0<br />NAME: Owensboro, KY Metro Area<br />popE: 117987","incomeE: 28959<br />commuteE: 25.5<br />NAME: Ocala, FL Metro Area<br />popE: 348371","incomeE: 40032<br />commuteE: 22.7<br />NAME: Ocean City, NJ Metro Area<br />popE: 93705","incomeE: 40711<br />commuteE: 23.1<br />NAME: Odessa, TX Metro Area<br />popE: 158342","incomeE: 40745<br />commuteE: 22.7<br />NAME: Ogden-Clearfield, UT Metro Area<br />popE: 652744","incomeE: 37176<br />commuteE: 22.7<br />NAME: Oklahoma City, OK Metro Area<br />popE: 1369759","incomeE: 44021<br />commuteE: 26.3<br />NAME: Olympia-Tumwater, WA Metro Area<br />popE: 274684","incomeE: 41974<br />commuteE: 20.3<br />NAME: Omaha-Council Bluffs, NE-IA Metro Area<br />popE: 922891","incomeE: 41777<br />commuteE: 26.8<br />NAME: Oxnard-Thousand Oaks-Ventura, CA Metro Area<br />popE: 848112","incomeE: 35363<br />commuteE: 24.8<br />NAME: Palm Bay-Melbourne-Titusville, FL Metro Area<br />popE: 576808","incomeE: 32423<br />commuteE: 23.3<br />NAME: Panama City, FL Metro Area<br />popE: 198537","incomeE: 32424<br />commuteE: 21.2<br />NAME: Parkersburg-Vienna, WV Metro Area<br />popE: 91353","incomeE: 35194<br />commuteE: 24.8<br />NAME: Pensacola-Ferry Pass-Brent, FL Metro Area<br />popE: 481964","incomeE: 39638<br />commuteE: 20.4<br />NAME: Peoria, IL Metro Area<br />popE: 374426","incomeE: 46260<br />commuteE: 29.9<br />NAME: Philadelphia-Camden-Wilmington, PA-NJ-DE-MD Metro Area<br />popE: 6069448","incomeE: 41143<br />commuteE: 24.9<br />NAME: Portland-South Portland, ME Metro Area<br />popE: 529323","incomeE: 42148<br />commuteE: 26.9<br />NAME: Portland-Vancouver-Hillsboro, OR-WA Metro Area<br />popE: 2417931","incomeE: 32166<br />commuteE: 26.8<br />NAME: Port St. Lucie, FL Metro Area<br />popE: 463172","incomeE: 39482<br />commuteE: 26.4<br />NAME: Phoenix-Mesa-Scottsdale, AZ Metro Area<br />popE: 4673634","incomeE: 32015<br />commuteE: 22.0<br />NAME: Pine Bluff, AR Metro Area<br />popE: 92345","incomeE: 41387<br />commuteE: 26.8<br />NAME: Pittsburgh, PA Metro Area<br />popE: 2339941","incomeE: 38137<br />commuteE: 19.9<br />NAME: Pittsfield, MA Metro Area<br />popE: 127328","incomeE: 31949<br />commuteE: 17.5<br />NAME: Pocatello, ID Metro Area<br />popE: 85065","incomeE: 16743<br />commuteE: 24.6<br />NAME: Ponce, PR Metro Area<br />popE: 307093","incomeE: 30501<br />commuteE: 23.4<br />NAME: Prescott, AZ Metro Area<br />popE: 224645","incomeE: 43640<br />commuteE: 26.0<br />NAME: Providence-Warwick, RI-MA Metro Area<br />popE: 1615516","incomeE: 39824<br />commuteE: 21.8<br />NAME: Provo-Orem, UT Metro Area<br />popE: 601388","incomeE: 34246<br />commuteE: 22.0<br />NAME: Pueblo, CO Metro Area<br />popE: 164685","incomeE: 28959<br />commuteE: 24.9<br />NAME: Punta Gorda, FL Metro Area<br />popE: 176954","incomeE: 40753<br />commuteE: 24.3<br />NAME: Racine, WI Metro Area<br />popE: 195398","incomeE: 43914<br />commuteE: 26.2<br />NAME: Raleigh, NC Metro Area<br />popE: 1302632","incomeE: 34146<br />commuteE: 18.6<br />NAME: Rapid City, SD Metro Area<br />popE: 145291","incomeE: 40310<br />commuteE: 24.9<br />NAME: Reading, PA Metro Area<br />popE: 416642","incomeE: 34258<br />commuteE: 20.4<br />NAME: Redding, CA Metro Area<br />popE: 179085","incomeE: 37970<br />commuteE: 21.6<br />NAME: Reno, NV Metro Area<br />popE: 454427","incomeE: 42022<br />commuteE: 25.2<br />NAME: Richmond, VA Metro Area<br />popE: 1281530","incomeE: 36251<br />commuteE: 32.4<br />NAME: Riverside-San Bernardino-Ontario, CA Metro Area<br />popE: 4518699","incomeE: 37620<br />commuteE: 24.1<br />NAME: Roanoke, VA Metro Area<br />popE: 313291","incomeE: 45214<br />commuteE: 19.9<br />NAME: Rochester, MN Metro Area<br />popE: 216035","incomeE: 40108<br />commuteE: 21.4<br />NAME: Rochester, NY Metro Area<br />popE: 1074667","incomeE: 36298<br />commuteE: 23.3<br />NAME: Rockford, IL Metro Area<br />popE: 339780","incomeE: 31282<br />commuteE: 22.3<br />NAME: Rocky Mount, NC Metro Area<br />popE: 147335","incomeE: 32021<br />commuteE: 22.9<br />NAME: Rome, GA Metro Area<br />popE: 96824","incomeE: 42519<br />commuteE: 27.2<br />NAME: Sacramento--Roseville--Arden-Arcade, CA Metro Area<br />popE: 2291738","incomeE: 32882<br />commuteE: 21.9<br />NAME: Saginaw, MI Metro Area<br />popE: 192778","incomeE: 36153<br />commuteE: 24.6<br />NAME: Salisbury, MD-DE Metro Area<br />popE: 399013","incomeE: 40119<br />commuteE: 22.5<br />NAME: Salt Lake City, UT Metro Area<br />popE: 1185990","incomeE: 33926<br />commuteE: 17.7<br />NAME: San Angelo, TX Metro Area<br />popE: 118990","incomeE: 35957<br />commuteE: 26.3<br />NAME: San Antonio-New Braunfels, TX Metro Area<br />popE: 2426204","incomeE: 42233<br />commuteE: 26.0<br />NAME: San Diego-Carlsbad, CA Metro Area<br />popE: 3302833","incomeE: 55525<br />commuteE: 33.6<br />NAME: San Francisco-Oakland-Hayward, CA Metro Area<br />popE: 4673221","incomeE: 16568<br />commuteE: 25.5<br />NAME: San Germán, PR Metro Area<br />popE: 127488","incomeE: 60983<br />commuteE: 28.9<br />NAME: San Jose-Sunnyvale-Santa Clara, CA Metro Area<br />popE: 1981616","incomeE: 20044<br />commuteE: 31.2<br />NAME: San Juan-Carolina-Caguas, PR Metro Area<br />popE: 2142392","incomeE: 39458<br />commuteE: 21.2<br />NAME: St. Cloud, MN Metro Area<br />popE: 196598","incomeE: 31913<br />commuteE: 17.5<br />NAME: St. George, UT Metro Area<br />popE: 160537","incomeE: 33893<br />commuteE: 18.8<br />NAME: St. Joseph, MO-KS Metro Area<br />popE: 126779","incomeE: 41340<br />commuteE: 25.8<br />NAME: St. Louis, MO-IL Metro Area<br />popE: 2805551","incomeE: 33305<br />commuteE: 23.9<br />NAME: Salem, OR Metro Area<br />popE: 416980","incomeE: 31806<br />commuteE: 22.7<br />NAME: Salinas, CA Metro Area<br />popE: 433212","incomeE: 41730<br />commuteE: 22.2<br />NAME: San Luis Obispo-Paso Robles-Arroyo Grande, CA Metro Area<br />popE: 281455","incomeE: 41844<br />commuteE: 27.0<br />NAME: Santa Cruz-Watsonville, CA Metro Area<br />popE: 273765","incomeE: 36281<br />commuteE: 22.3<br />NAME: Santa Fe, NM Metro Area<br />popE: 148917","incomeE: 37204<br />commuteE: 19.8<br />NAME: Santa Maria-Santa Barbara, CA Metro Area<br />popE: 443738","incomeE: 41245<br />commuteE: 25.4<br />NAME: Santa Rosa, CA Metro Area<br />popE: 501317","incomeE: 36871<br />commuteE: 24.3<br />NAME: Savannah, GA Metro Area<br />popE: 381623","incomeE: 36173<br />commuteE: 22.1<br />NAME: Scranton--Wilkes-Barre--Hazleton, PA Metro Area<br />popE: 556926","incomeE: 50957<br />commuteE: 30.7<br />NAME: Seattle-Tacoma-Bellevue, WA Metro Area<br />popE: 3809717","incomeE: 30186<br />commuteE: 22.4<br />NAME: Sebastian-Vero Beach, FL Metro Area<br />popE: 150984","incomeE: 24468<br />commuteE: 19.9<br />NAME: Sebring, FL Metro Area<br />popE: 102101","incomeE: 40266<br />commuteE: 18.0<br />NAME: Sheboygan, WI Metro Area<br />popE: 115205","incomeE: 35035<br />commuteE: 25.1<br />NAME: Sherman-Denison, TX Metro Area<br />popE: 128560","incomeE: 32444<br />commuteE: 22.0<br />NAME: Shreveport-Bossier City, LA Metro Area<br />popE: 441339","incomeE: 30634<br />commuteE: 20.6<br />NAME: Sierra Vista-Douglas, AZ Metro Area<br />popE: 126279","incomeE: 37064<br />commuteE: 18.0<br />NAME: Sioux City, IA-NE-SD Metro Area<br />popE: 168677","incomeE: 39641<br />commuteE: 18.4<br />NAME: Sioux Falls, SD Metro Area<br />popE: 255438","incomeE: 35921<br />commuteE: 21.6<br />NAME: South Bend-Mishawaka, IN-MI Metro Area<br />popE: 320700","incomeE: 32802<br />commuteE: 23.0<br />NAME: Spartanburg, SC Metro Area<br />popE: 329839","incomeE: 41683<br />commuteE: 20.2<br />NAME: Springfield, IL Metro Area<br />popE: 210028","incomeE: 41485<br />commuteE: 22.8<br />NAME: Springfield, MA Metro Area<br />popE: 630275","incomeE: 33665<br />commuteE: 21.9<br />NAME: Springfield, MO Metro Area<br />popE: 458834","incomeE: 33574<br />commuteE: 22.5<br />NAME: Springfield, OH Metro Area<br />popE: 135198","incomeE: 39859<br />commuteE: 20.3<br />NAME: State College, PA Metro Area<br />popE: 161443","incomeE: 36399<br />commuteE: 23.3<br />NAME: Staunton-Waynesboro, VA Metro Area<br />popE: 121079","incomeE: 37171<br />commuteE: 33.2<br />NAME: Stockton-Lodi, CA Metro Area<br />popE: 732212","incomeE: 30817<br />commuteE: 22.4<br />NAME: Sumter, SC Metro Area<br />popE: 106995","incomeE: 36779<br />commuteE: 22.2<br />NAME: Spokane-Spokane Valley, WA Metro Area<br />popE: 555308","incomeE: 41210<br />commuteE: 21.2<br />NAME: Syracuse, NY Metro Area<br />popE: 654705"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,139,1)","opacity":1,"size":[6.19472154591903,11.0803697676654,5.22007534117096,5.08792932993688,4.87122536170719,6.91879914729421,5.56915406127713,6.15229887045033,4.75049313231205,7.9377543932641,7.86279101596631,5.60942947297249,5.52740292732801,5.04993290289232,6.40246771334969,7.86806297109666,5.84787023946798,14.2190039301009,5.21894953158686,4.67769520863731,5.11077178178823,9.2449595632108,6.47636961340089,6.02859550357524,4.78639510354982,9.84260736793679,14.7549582019128,5.81090967340554,6.40156265469805,5.90386989512052,5.2749265009348,7.59816024411576,4.48673179566777,4.99184360405386,6.56939158354879,5.49084307211898,5.43278399290778,5.42743361686887,7.09651224900508,6.72365078051861,6.52944410912105,5.75377971494594,5.47709105421504,9.89400721112366,4.8573540009264,4.9310449141847,5.00770536290687,4.15867634289735,4.75368875765698,6.62601690238225,4.71808170188853,5.98993691892445,6.11221978924706,6.44340497607297,5.03863049241982,9.69434852951464,4.94084253593872,5.26372620405263,5.18891819029731,4.71156987121334,5.14736048252961,6.84856937917267,4.93756782569959,8.82465112491109,5.36000616006889,5.16593555727287,5.09559433907197,5.40092513230622,4.97725310807908,5.21818397590096,5.908759260766,7.19176687071826,5.10875858486058,4.8864691906902,7.62616142500677,7.69431850756101,5.11409127958494,7.51784043402159,7.26974737163602,4.98519090258262,5.49033532159808,4.73200661439356,19.161139348993,8.47502296329467,5.93205365508483,5.70143527476719,5.55112625607504,5.1215801834284,7.03824250491743,6.3070207517537,4.67108932601371,4.68369829925065,4.87388851290513,4.89430621470695,5.71418081354985,4.65159800629889,6.26589488163596,6.14170212790828,4.82168782831882,5.57565343178399,5.30215228479286,6.44113448941729,5.42329226091036,13.906386030941,5.7377728011269,5.14980726064814,6.8892158721406,9.77086024318223,7.63214549596026,10.7838472268282,5.09961032082947,5.46837355276138,7.50590657602001,4.97667716158265,5.48485038623852,5.282913073641,5.2124261456769,5.61943115867747,8.20352799559226,4.94681208072938,5.29301308497008,4.72893612896385,6.30207602717536,4.86595367321953,5.33342527140825,5.19478432166555,4.51317550379891,7.16408841817359,13.0108903461751,5.96470687236861,5.23106947180197,5.70983802721616,7.77210284200637,6.34452868629642,4.83498430903344,4.65380338102234,4.91032429116479,3.77952755905512,4.46385642289813,5.73674800166269,5.11313122205102,5.72487336204023,4.19787241059118,5.33735134059303,5.09448455848239,4.81963176585551,5.80394453817206,4.81608648976747,4.98258057057627,4.85751187734255,4.83899059120864,5.03646612954313,7.02856435862377,4.99030591935227,7.07790135421977,7.7596779505439,5.64782606751826,6.42112769814756,6.74529559345366,5.2266013814637,5.43699890264444,5.59899873676222,5.48747444581236,7.33268075247565,10.3617776368906,5.55732881982392,6.76502607058055,4.65947077568062,16.8122824981019,8.17206795832512,5.15820686726092,5.49129834910482,4.79056735938125,6.27120978746015,7.22890330640831,5.53792728325536,9.93379561351733,5.80280717420437,4.87401127113293,9.77596325598913,5.11215030988124,5.66984933778685,7.21221096987531,5.25813361380099,7.47458134346018,5.9094700414167,4.48044744655209,9.7644450538237,6.44905764619679,4.5748705423084,5.72886105479074,4.67523871127166,15.1367024521803,5.04174235797714,4.43438869902143,5.43850047542453,6.20441452257101,7.44044229064643,5.10330292409299,4.74508174989949,7.0036808146624,10.8563227061754,7.00209142015234,12.5178917817337,5.07370239819824,5.24784249101381,4.65036467093019,5.78514691162497,6.78430807906715,5.20301921351952,5.19696601416826,5.28038491040549,4.5279932874601,7.53490104099471,4.15147379166701,5.77147976397114,6.15275179745258,5.939712879803,4.67920969190515,5.09164115425242,5.41400845214322,5.58778979052617,4.92296623664466,6.21409098130394,6.68711538239882,5.01890678135599,6.30089694419024,5.42607426772869,5.06754909029721,4.70533153474296,6.03383021198146,5.79485431934636,7.84718077328076,4.7113488224914,5.79290679529846,5.37157556386128,4.70250227892884,6.37873728822299,4.91394613968703,4.895590984887,4.70219169602449,4.51579561808478,5.08768286985938,8.00340131423811,4.52488748274705,4.47856650039237,5.85580551817669,5.95102320679951,7.32905658150423,5.26331579093822,7.63400489906851,6.2358758741367,5.71369001630529,4.94660489020952,5.08820996404815,6.81214196505884,4.96435888614406,8.32793474941564,5.07923407378482,6.13934252100368,5.45168081265992,4.45931282715348,4.4169787928634,5.21278864058177,5.0394767140207,4.66559734476896,5.4529818973487,5.47143084632705,8.5894534743078,5.74022282554322,4.6150174606452,7.55307144373978,14.1609837867866,4.78185705072467,4.49931009907475,5.21693206832075,9.0000571500247,11.7010926786019,4.82926621684924,6.31964723229035,6.72655161392471,5.27040962046373,5.08563408479832,6.17045017079045,5.01072807685188,4.83779791619167,4.89482833108754,4.82613020014357,5.2369503098472,6.43384913218695,5.02116667841047,6.13395818764734,9.47312765556047,4.90769951619504,7.57661463321517,8.43357139328723,22.6771653543307,5.12020467077217,7.39948293864357,5.73933641664234,10.3305921769151,5.217667151133,4.84622779573638,6.07403724395512,4.61790691955807,5.14361642822521,7.05322320191195,8.63351039220574,5.76567995140546,7.72367421803799,7.55003922649732,6.83841998982571,5.38600238664156,4.59239162960535,6.54681124273118,6.1735835989857,14.1596930294162,6.69606873139878,10.2862404295918,6.48530531497678,12.8759156027631,4.60324956153186,10.1779850538735,4.9219710049848,4.51987173945434,5.90681496790542,5.52550590999267,9.06757587356823,6.90956437883767,5.18464754086167,5.26079045948416,5.36840505339801,8.50802487540744,5.05504810675135,6.32662981877225,5.27362022944606,6.45620122742211,8.46788351297585,12.7220600108113,5.93275258664531,5.48076456566546,8.05446541989057,6.04025354786812,5.06932108621729,4.65059091314254,10.1101504438286,5.35356662691128,6.26386596298078,8.28166594145334,4.85461656970318,10.2976184348361,11.407684591858,12.8755089393712,4.92322469839333,9.65502706030505,9.89520531797148,5.3751552059075,5.15795347954388,4.91765877074196,10.7995592433957,6.32781808382895,6.38424489689199,5.79598284377285,5.76153135633568,5.08026046711348,6.42019172530535,6.60875608261497,6.20035922499383,6.7796395141714,11.9812784437449,5.09441644328882,4.70325888726968,4.82260701152697,4.9315892528869,6.41204220505873,4.91371715164747,5.20986732354139,5.67690548408515,5.9633538479587,6.00051977349387,5.44883953801109,6.99116116743833,6.47090742869016,4.98208910603919,5.16382789470482,4.8718815090213,7.26386580418392,4.7495517821257,6.77480519409565,7.05858398396521],"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,139,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[16048,16616.7974683544,17185.5949367089,17754.3924050633,18323.1898734177,18891.9873417722,19460.7848101266,20029.582278481,20598.3797468354,21167.1772151899,21735.9746835443,22304.7721518987,22873.5696202532,23442.3670886076,24011.164556962,24579.9620253165,25148.7594936709,25717.5569620253,26286.3544303797,26855.1518987342,27423.9493670886,27992.746835443,28561.5443037975,29130.3417721519,29699.1392405063,30267.9367088608,30836.7341772152,31405.5316455696,31974.3291139241,32543.1265822785,33111.9240506329,33680.7215189873,34249.5189873418,34818.3164556962,35387.1139240506,35955.9113924051,36524.7088607595,37093.5063291139,37662.3037974684,38231.1012658228,38799.8987341772,39368.6962025316,39937.4936708861,40506.2911392405,41075.0886075949,41643.8860759494,42212.6835443038,42781.4810126582,43350.2784810127,43919.0759493671,44487.8734177215,45056.670886076,45625.4683544304,46194.2658227848,46763.0632911392,47331.8607594937,47900.6582278481,48469.4556962025,49038.253164557,49607.0506329114,50175.8481012658,50744.6455696203,51313.4430379747,51882.2405063291,52451.0379746835,53019.835443038,53588.6329113924,54157.4303797468,54726.2278481013,55295.0253164557,55863.8227848101,56432.6202531646,57001.417721519,57570.2151898734,58139.0126582279,58707.8101265823,59276.6075949367,59845.4050632911,60414.2025316456,60983],"y":[19.6887962997068,19.7791760533396,19.8695558069724,19.9599355606052,20.050315314238,20.1406950678708,20.2310748215036,20.3214545751364,20.4118343287692,20.502214082402,20.5925938360348,20.6829735896676,20.7733533433004,20.8637330969332,20.954112850566,21.0444926041988,21.1348723578316,21.2252521114644,21.3156318650972,21.40601161873,21.4963913723628,21.5867711259956,21.6771508796284,21.7675306332612,21.857910386894,21.9482901405268,22.0386698941596,22.1290496477924,22.2194294014252,22.309809155058,22.4001889086908,22.4905686623235,22.5809484159563,22.6713281695891,22.7617079232219,22.8520876768547,22.9424674304875,23.0328471841203,23.1232269377531,23.2136066913859,23.3039864450187,23.3943661986515,23.4847459522843,23.5751257059171,23.6655054595499,23.7558852131827,23.8462649668155,23.9366447204483,24.0270244740811,24.1174042277139,24.2077839813467,24.2981637349795,24.3885434886123,24.4789232422451,24.5693029958779,24.6596827495107,24.7500625031435,24.8404422567763,24.9308220104091,25.0212017640419,25.1115815176747,25.2019612713075,25.2923410249403,25.3827207785731,25.4731005322059,25.5634802858387,25.6538600394715,25.7442397931043,25.8346195467371,25.9249993003699,26.0153790540027,26.1057588076355,26.1961385612683,26.2865183149011,26.3768980685339,26.4672778221667,26.5576575757995,26.6480373294323,26.7384170830651,26.8287968366979],"text":["incomeE: 16048.00<br />commuteE: 19.68880<br />popE: 1","incomeE: 16616.80<br />commuteE: 19.77918<br />popE: 1","incomeE: 17185.59<br />commuteE: 19.86956<br />popE: 1","incomeE: 17754.39<br />commuteE: 19.95994<br />popE: 1","incomeE: 18323.19<br />commuteE: 20.05032<br />popE: 1","incomeE: 18891.99<br />commuteE: 20.14070<br />popE: 1","incomeE: 19460.78<br />commuteE: 20.23107<br />popE: 1","incomeE: 20029.58<br />commuteE: 20.32145<br />popE: 1","incomeE: 20598.38<br />commuteE: 20.41183<br />popE: 1","incomeE: 21167.18<br />commuteE: 20.50221<br />popE: 1","incomeE: 21735.97<br />commuteE: 20.59259<br />popE: 1","incomeE: 22304.77<br />commuteE: 20.68297<br />popE: 1","incomeE: 22873.57<br />commuteE: 20.77335<br />popE: 1","incomeE: 23442.37<br />commuteE: 20.86373<br />popE: 1","incomeE: 24011.16<br />commuteE: 20.95411<br />popE: 1","incomeE: 24579.96<br />commuteE: 21.04449<br />popE: 1","incomeE: 25148.76<br />commuteE: 21.13487<br />popE: 1","incomeE: 25717.56<br />commuteE: 21.22525<br />popE: 1","incomeE: 26286.35<br />commuteE: 21.31563<br />popE: 1","incomeE: 26855.15<br />commuteE: 21.40601<br />popE: 1","incomeE: 27423.95<br />commuteE: 21.49639<br />popE: 1","incomeE: 27992.75<br />commuteE: 21.58677<br />popE: 1","incomeE: 28561.54<br />commuteE: 21.67715<br />popE: 1","incomeE: 29130.34<br />commuteE: 21.76753<br />popE: 1","incomeE: 29699.14<br />commuteE: 21.85791<br />popE: 1","incomeE: 30267.94<br />commuteE: 21.94829<br />popE: 1","incomeE: 30836.73<br />commuteE: 22.03867<br />popE: 1","incomeE: 31405.53<br />commuteE: 22.12905<br />popE: 1","incomeE: 31974.33<br />commuteE: 22.21943<br />popE: 1","incomeE: 32543.13<br />commuteE: 22.30981<br />popE: 1","incomeE: 33111.92<br />commuteE: 22.40019<br />popE: 1","incomeE: 33680.72<br />commuteE: 22.49057<br />popE: 1","incomeE: 34249.52<br />commuteE: 22.58095<br />popE: 1","incomeE: 34818.32<br />commuteE: 22.67133<br />popE: 1","incomeE: 35387.11<br />commuteE: 22.76171<br />popE: 1","incomeE: 35955.91<br />commuteE: 22.85209<br />popE: 1","incomeE: 36524.71<br />commuteE: 22.94247<br />popE: 1","incomeE: 37093.51<br />commuteE: 23.03285<br />popE: 1","incomeE: 37662.30<br />commuteE: 23.12323<br />popE: 1","incomeE: 38231.10<br />commuteE: 23.21361<br />popE: 1","incomeE: 38799.90<br />commuteE: 23.30399<br />popE: 1","incomeE: 39368.70<br />commuteE: 23.39437<br />popE: 1","incomeE: 39937.49<br />commuteE: 23.48475<br />popE: 1","incomeE: 40506.29<br />commuteE: 23.57513<br />popE: 1","incomeE: 41075.09<br />commuteE: 23.66551<br />popE: 1","incomeE: 41643.89<br />commuteE: 23.75589<br />popE: 1","incomeE: 42212.68<br />commuteE: 23.84626<br />popE: 1","incomeE: 42781.48<br />commuteE: 23.93664<br />popE: 1","incomeE: 43350.28<br />commuteE: 24.02702<br />popE: 1","incomeE: 43919.08<br />commuteE: 24.11740<br />popE: 1","incomeE: 44487.87<br />commuteE: 24.20778<br />popE: 1","incomeE: 45056.67<br />commuteE: 24.29816<br />popE: 1","incomeE: 45625.47<br />commuteE: 24.38854<br />popE: 1","incomeE: 46194.27<br />commuteE: 24.47892<br />popE: 1","incomeE: 46763.06<br />commuteE: 24.56930<br />popE: 1","incomeE: 47331.86<br />commuteE: 24.65968<br />popE: 1","incomeE: 47900.66<br />commuteE: 24.75006<br />popE: 1","incomeE: 48469.46<br />commuteE: 24.84044<br />popE: 1","incomeE: 49038.25<br />commuteE: 24.93082<br />popE: 1","incomeE: 49607.05<br />commuteE: 25.02120<br />popE: 1","incomeE: 50175.85<br />commuteE: 25.11158<br />popE: 1","incomeE: 50744.65<br />commuteE: 25.20196<br />popE: 1","incomeE: 51313.44<br />commuteE: 25.29234<br />popE: 1","incomeE: 51882.24<br />commuteE: 25.38272<br />popE: 1","incomeE: 52451.04<br />commuteE: 25.47310<br />popE: 1","incomeE: 53019.84<br />commuteE: 25.56348<br />popE: 1","incomeE: 53588.63<br />commuteE: 25.65386<br />popE: 1","incomeE: 54157.43<br />commuteE: 25.74424<br />popE: 1","incomeE: 54726.23<br />commuteE: 25.83462<br />popE: 1","incomeE: 55295.03<br />commuteE: 25.92500<br />popE: 1","incomeE: 55863.82<br />commuteE: 26.01538<br />popE: 1","incomeE: 56432.62<br />commuteE: 26.10576<br />popE: 1","incomeE: 57001.42<br />commuteE: 26.19614<br />popE: 1","incomeE: 57570.22<br />commuteE: 26.28652<br />popE: 1","incomeE: 58139.01<br />commuteE: 26.37690<br />popE: 1","incomeE: 58707.81<br />commuteE: 26.46728<br />popE: 1","incomeE: 59276.61<br />commuteE: 26.55766<br />popE: 1","incomeE: 59845.41<br />commuteE: 26.64804<br />popE: 1","incomeE: 60414.20<br />commuteE: 26.73842<br />popE: 1","incomeE: 60983.00<br />commuteE: 26.82880<br />popE: 1"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(255,140,0,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":33.8729763387298},"plot_bgcolor":"rgba(255,255,255,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[13801.25,63229.75],"tickmode":"array","ticktext":["20000","30000","40000","50000","60000"],"tickvals":[20000,30000,40000,50000,60000],"categoryorder":"array","categoryarray":["20000","30000","40000","50000","60000"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":"<b> Median Household Earnings <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[14.215,40.285],"tickmode":"array","ticktext":["15","20","25","30","35","40"],"tickvals":[15,20,25,30,35,40],"categoryorder":"array","categoryarray":["15","20","25","30","35","40"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(201,201,201,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":"<b> Mean Travel Time to Work <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":1100,"height":500,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"371854c22985":{"x":{},"y":{},"label":{},"size":{},"type":"scatter"},"3718149c71cd":{"x":{},"y":{},"label":{},"size":{}}},"cur_data":"371854c22985","visdat":{"371854c22985":["function (y) ","x"],"3718149c71cd":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> --- class: inverse,center, middle # The Rosen-Roback Model --- # Consumer Analysis * We extend the consumer's utility function to include amenities `\(a\)`. The same way we simplified housing as "quantity of floor space" `\((q)\)`, we treat `\(a\)` as a single index that represents lower crime rates, nice weather, proximity to the ocean, etc. Consumers get utility from amenities. * All consumers have the same preferences that can be represented by `\(U(.)\)`. Including amenities, the new consumer's utility function is `\(U(c,q,a)\)`. * We assume that there are no costs of changing residences across cities, and we ignore intracity commuting costs * Cities vary according to the quantity of an endowed amenity `\(a\)`. Consumers in a given location (with amenities `\(a\)`) will choose `\(c\)` and `\(q\)` to maximize utility given their budget constraint `\(y=pq+c\)` * Associated with this maximization problem is the indirect utility function `\(V(.)\)`. It is easier to see how incomes and prices vary with amenities **considering the utility level that consumers achieve earning `\(y\)` and paying `\(p\)` for housing: `\(V(y,p,a)\)`** * `\(V(.) \downarrow\)` when `\(p \uparrow\)`, `\(y \downarrow\)` or `\(a \downarrow\)` * `\(V(.) \uparrow\)` when `\(p \downarrow\)`, `\(y \uparrow\)` or `\(a \uparrow\)` --- # Consumer Analysis .pull-left[ * Consumers have the same preferences and are free to move without costs. Hence, also for the analysis across cities, we rely on the idea of spatial equilibrium * Spatial equilibrium implies consumers equally well off across regions: `\(V(y,p,a)=\bar{u}\)`. If some location offers higher utility levels compared to others, workers will move there and push incomes down or housing prices up until utility levels are equalized * The analysis is done with indifference curves that show different combinations of `\(p\)` and `\(y\)` that yield the same utility `\(\bar{u}\)`, conditional on a given amenity level ] .pull-right[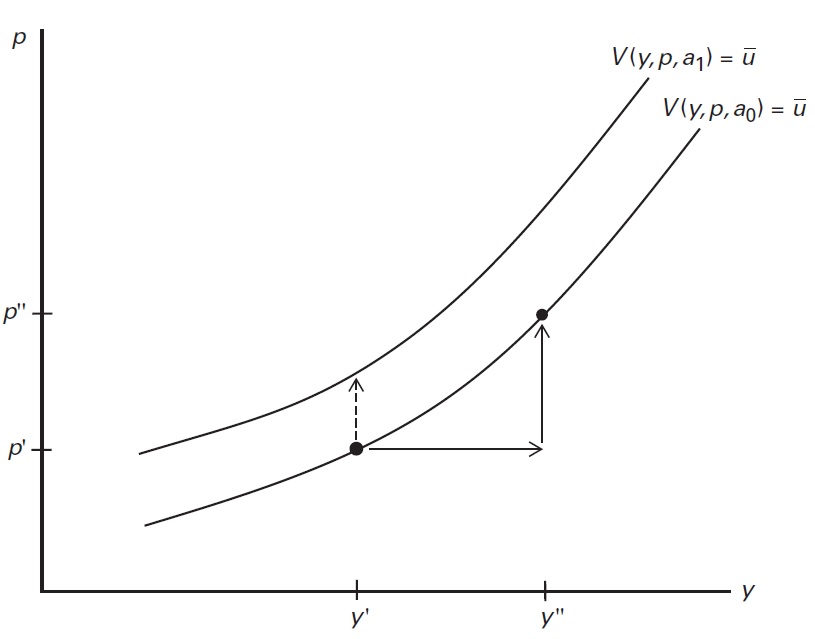] --- # Firm Analysis .pull-left[ * Firms use labor `\(y\)` and "real estate" (floor space) `\(p\)` to produce the commodity `\(c\)` (bread). The price of floor space is common across residential and business uses, and we assume constant returns to scale - the cost per unit of bread is the same, no matter how much output a firm produces * Costs may also depend on amenities. Thus, `\(C(y,p,a)\)`. `\(C\)` is increasing in `\(y\)` and `\(p\)`, and may increase or decrease with amenities. It is also possible that `\(C\)` is independent of `\(a\)`. * Spatial equilibrium implies firm profits equal across regions. The zero-profit condition holds when `\(C(y,p,a)\)` is equal to `\(1\)` - the cost of a unit of c. This condition generates iso-profit curves: given the amenity level, which combinations of `\(y\)` and `\(p\)` lead to zero profit ] .pull-right[] --- # High-amenity x Low-amenity areas <br/ > * Putting indifference curves and iso-profit curves together, one can answer the main question of interest: How do real-estate prices and incomes differ between high-amenity and low-amenity regions? * There are three possible cases: 1. Amenities **do not affect** firms' costs - Only one iso-profit curve 2. Amenities **decrease** firms' costs - Iso-profit curve moves upward - Example: Lack of snow storms 3. Amenities **increase** firms' costs - Iso-profit curve moves downward - Example: Clean air --- # Case 1 .pull-left[ * In the low-amenity area `\(a_{0}\)`, the intersection point occurs at `\(p_{0}\)` and `\(y_{0}\)`. Those values satisfy two requirements. First, paying `\(p_{0}\)` for housing and earning `\(y_{0}\)`, consumers are enjoying the common utility level across regions `\(\underline{u}\)`. * Second, firms earn zero profit since the point `\(p_{0}\)`, `\(y_{0}\)` also lies on the iso-profit curve. The same reasoning can be applied to high-amenity area `\(a_{1}\)` * As one can see, the high-amenity region has a higher real-estate price and lower-income level compared to the low-amenity region ] .pull-right[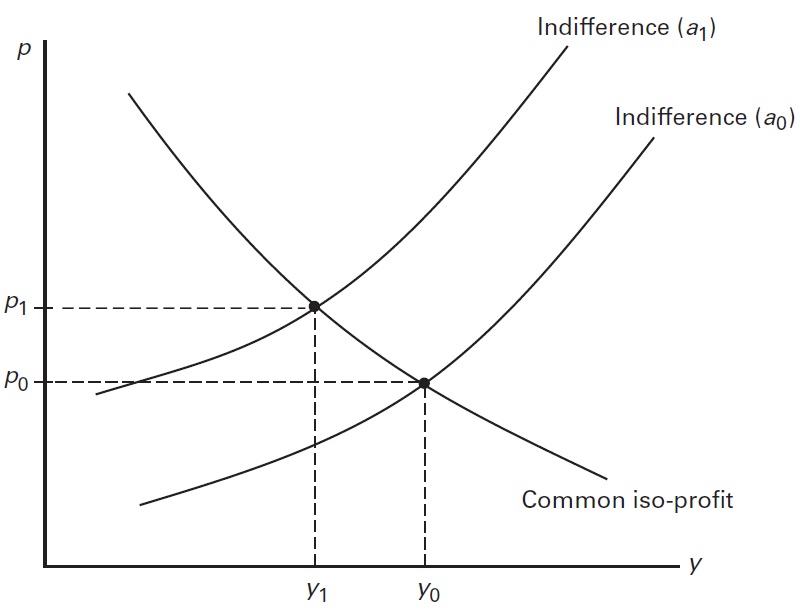] --- # Case 2 .pull-left[ * With firm costs decreasing in consumer amenity (no winter storm), there will be two iso-profit curves - in the high amenity area `\(a_{1}\)`, the iso-profit curve shifts upward * Depending on the shift in the iso-profit curve (i.e., depending on how much amenities decrease the firm's costs), the high-amenity region can have both higher incomes and higher housing prices (as you see in the figure), or lower incomes and higher housing prices ] .pull-right[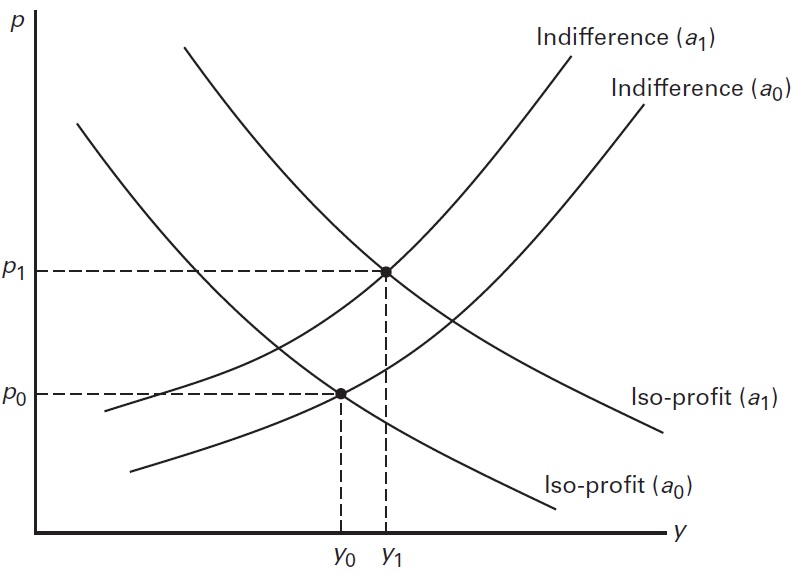] --- # Case 3 .pull-left[ * In case the amenity is "unproductive", the iso-profit curve shifts downward. For instance, clean air is a valuable amenity to consumers but demands firms to adopt new nonpolluting technologies, and that might increase firm's cost * Again, depending on how much the amenity increases costs - i.e., the shift in the iso-profit curve -, the high-amenity region can have both lower incomes and housing prices (as you see in the figure), or lower incomes and higher housing prices * To summarize, when amenities have only a small role on firm costs, the pattern we saw on case 1 will prevail: the higher amenity region will offer higher housing prices and lower wages ] .pull-right[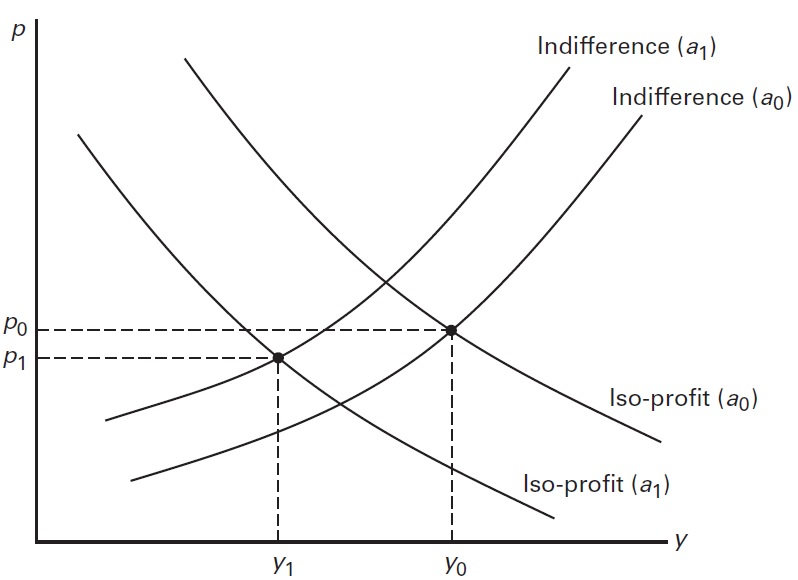] --- # Quality of Life in the US <iframe src="maps/qol.html" style="width: 1200px; height: 500px; border: 5px" alt=""> --- # Housing Supply and Productivity Shocks <style type="text/css"> .pull-left2 { float: left; width: 39%; } .pull-right2 { float: right; width: 59%; } .pull-right2 ~ p { clear: both; } </style> .pull-left2[ * In reality, cities differ in terms of housing supply. For instance, different regulatory environment (or natural boundaries) might impact developers, who would respond differently to increase in demand for housing * For instance, consider a productivity shock in both cities A and B. City B has an inelastic supply curve, and when demand shows up, that is translated to higher housing prices. * When the supply curve is very elastic (Sun belt metros), you might see fast-growing areas without increasing housing prices ] .pull-right2[ <div id="htmlwidget-d9aff056d637fa90c56c" style="width:650px;height:500px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-d9aff056d637fa90c56c">{"x":{"data":[{"visible":false,"showlegend":false,"xaxis":null,"yaxis":null,"hoverinfo":"text","frame":null},{"x":[60,120],"y":[30,60],"text":"x: 60<br />y: 30<br />xend: 120<br />yend: 60<br />colour: Supply in city A","type":"scatter","mode":"lines","line":{"width":4.53543307086614,"color":"rgba(0,191,196,1)","dash":"solid"},"hoveron":"points","name":"Supply in city A","legendgroup":"Supply in city A","showlegend":true,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[60,100],"y":[30,90],"text":"x: 60<br />y: 30<br />xend: 100<br />yend: 90<br />colour: Supply in city B","type":"scatter","mode":"lines","line":{"width":4.53543307086614,"color":"rgba(199,124,255,1)","dash":"solid"},"hoveron":"points","name":"Supply in city B","legendgroup":"Supply in city B","showlegend":true,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[60,60],"y":[0,30],"text":"x: 60<br />y: 0<br />xend: 60<br />yend: 30","type":"scatter","mode":"lines","line":{"width":4.91338582677165,"color":"rgba(0,0,0,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[20,120],"y":[66.6666666666667,0],"text":"intercept: 80<br />-2/3: -0.6666667<br />colour: Old Demand","type":"scatter","mode":"lines","line":{"width":4.53543307086614,"color":"rgba(124,174,0,1)","dash":"solid"},"hoveron":"points","name":"Old Demand","legendgroup":"Old Demand","showlegend":true,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[20,120],"y":[106.666666666667,40],"text":"intercept: 120<br />-2/3: -0.6666667<br />colour: New Demand","type":"scatter","mode":"lines","line":{"width":4.53543307086614,"color":"rgba(248,118,109,1)","dash":"solid"},"hoveron":"points","name":"New Demand","legendgroup":"New Demand","showlegend":true,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":48.4848484848485,"l":55.7907845579079},"plot_bgcolor":"rgba(255,255,255,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":19.9252801992528},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[20,120],"tickmode":"array","ticktext":["20","40","60","80","100","120"],"tickvals":[20,40,60,80,100,120],"categoryorder":"array","categoryarray":["20","40","60","80","100","120"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-7.30593607305936,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":19.9252801992528},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":"Housing Quantity","font":{"color":"rgba(0,0,0,1)","family":"","size":19.9252801992528}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[0,110],"tickmode":"array","ticktext":["0","20","40","60","80","100"],"tickvals":[0,20,40,60,80,100],"categoryorder":"array","categoryarray":["0","20","40","60","80","100"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-7.30593607305936,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":19.9252801992528},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(201,201,201,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":"Housing Price","font":{"color":"rgba(0,0,0,1)","family":"","size":19.9252801992528}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":true,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":24.906600249066},"y":0.91496062992126},"hovermode":"closest","width":650,"height":500,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"37183f7a50f5":{"type":"scatter"},"371820462bd2":{"x":{},"y":{},"xend":{},"yend":{},"colour":{}},"371815c732e5":{"x":{},"y":{},"xend":{},"yend":{},"colour":{}},"371838cd1cd1":{"x":{},"y":{},"xend":{},"yend":{}},"37185ab50ff":{"intercept":{},"slope":{},"colour":{}},"371810f6ad1":{"intercept":{},"slope":{},"colour":{}}},"cur_data":"37183f7a50f5","visdat":{"37183f7a50f5":["function (y) ","x"],"371820462bd2":["function (y) ","x"],"371815c732e5":["function (y) ","x"],"371838cd1cd1":["function (y) ","x"],"37185ab50ff":["function (y) ","x"],"371810f6ad1":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> ] --- # People and Prices Across Space The (more sophisticated) Rosen-Roback model serves as the basis for empirical work on cities. The spatial equilibrium model shows how **productivity, housing supply, and amenities** determine changes in **population, wages, and prices** across cities. When you solve the model, three intuitive (and estimable) equations come out, representing the primary relationships to understand urban change: `\begin{equation} Population=f(\underbrace{\text{Productivity}}_\text{+}, \underbrace{\text{Amenities}}_\text{+}, \underbrace{\text{Land Supply}}_\text{+}) \end{equation}` `\begin{equation} Income=f(\underbrace{\text{Productivity}}_\text{+}, \underbrace{\text{Amenities}}_\text{-}, \underbrace{\text{Land Supply}}_\text{-}) \end{equation}` `\begin{equation} Prices=f(\underbrace{\text{Productivity}}_\text{+}, \underbrace{\text{Amenities}}_\text{+}, \underbrace{\text{Land Supply}}_\text{-}) \end{equation}` The population rises with productivity, amenities, and land supply. Income is rising in productivity and falling in both amenities and land supply. Prices increase in productivity and amenities, and decline in land. Also, changes in population, income, and prices can identify amenities, productivity, and land supply changes. --- # The Rise of Sunbelt .pull-left[ * Over the past years, America's fastest-growing metro areas are Atlanta, Dallas, Phoenix, and Houston * Some areas added almost 1 million people between 2000 and 2010 * The figure relates the population growth between 2013 and 2015 * Different theories explain the rise of Sunbelt. Based on the Rosen-Roback model, one can raise three possibilities: 1. Increase in productivity (e.g., capital accumulation, improvements in political institutions) 2. Consumption of amenities (higher desire for mild winters, improvements in public service) 3. Local policies that support new construction of housing ] .pull-right[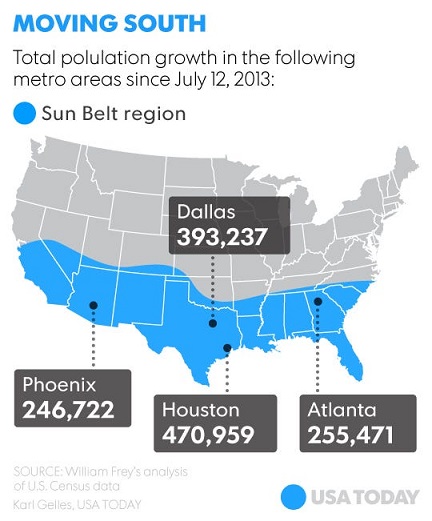] --- # The Rise of Sunbelt .pull-left[ * The rise of Sunbelt cities seems to be more related to a **very elastic housing supply** * The plentiful housing supply reflects the combination of abundant land, freeways, and pro-growth permitting. There is a high tolerance for new constructions there * One can emphasize the Sunbelt's rising productivity, but the combination of a growing population, stagnant wages, and declining housing prices suggest that amenity values were not increasing ] .pull-right[] --- # House Values and City Growth <div id="htmlwidget-ca8edad72733b359b2cd" style="width:1100px;height:500px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-ca8edad72733b359b2cd">{"x":{"data":[{"x":[0.0662555899056326,-0.0897005013548719,0.00602560705044098,-0.0670353850477893,0.0326916994550364,0.0906198301365905,0.0129560651701815,0.0384788498111047,-0.0171483551795168,0.085364434632757,0.133846865386656,0.0974126146121385,0.0560677642797276,0.0186704945901828,0.073156401080152,0.110260345031746,0.0976870543448367,0.0981812766251099,-0.00548506170426881,0.198040198449435,0.117074679835356,0.258552994468483,0.12287025268125,0.0451321889588629,0.0216295580542775,-0.040980342224067,0.0790252161193543,-0.0177046651749674,-0.0281533808377144,0.0831602587700337,0.116931277773816,0.173421949204804,0.118592862785919,-0.00870721193450338,0.0308451921281966,0.237862821825636,0.147889053255632,-0.0954845681676509,0.178637031412004,0.0638880453534726,0.0827845248847804,0.390672796498298,0.0944247732449329,0.0560839887310879,0.0959313566900027,0.141954133879692,0.00243941081416643,0.103627982110324,0.0550654884064381,-0.0177126566168964,0.225350027601769,0.0444695445497346,-0.0144904976945656,0.115501494464412,0.0629389464228186,0.072219735936769,-0.334959770661883,0.184254547681178,0.410020121489889,0.181832297751845,0.0700067639184273,0.117153704185157,0.00785466105213774,0.0411661030417128,0.0130078237580109,0.0869541978425278,0.0897880759745033,-0.0192412147364208,0.140575071937946,0.219756839189626,0.158276555182002,0.0876940139524639,0.127584774513634,0.0626381904969704,0.0921878080709192,0.155340494618369,0.0918705632107353,0.1015929627636,-0.00304809277657313,0.166180664678389,0.0766322386643866,-0.0316219477718346,-0.0281498794726657,0.0187070215876805,-0.0447259812530946,0.0199088755122059,-0.0209962935013672,0.249823443401643,0.150884926832078,0.154260798194101,-0.0308743368906375,0.0591325815833572,0.144292214663798,0.0503792031354259,0.015796712974855,0.152402851420814,0.0576351143190024,0.118769838806793,0.298729498160501,0.028662708696051,-0.0278452271831461,0.143268639640613,-0.0134932665373889,0.0704923449757219,-0.104865102978467,0.0286030410500919,0.206912277131182,0.0398972590904183,0.0912865735329668,0.175561934450198,0.0965504559639757,-0.0554934602317187,0.0340500060663585,0.0274609227421267,0.0295482466602514,0.164116555664988,-0.0255144451340902,0.0541297794117169,0.0935787810505935,-0.00204765973657344,0.0932674824284492,0.0979033401721163,-0.0150943593520598,0.0903467916218263,0.0474350807096998,0.0842454717351618,0.306133113647301,-0.00202862135585643,0.20167869285348,0.0554764166549576,0.0858146236423155,0.028820570415464,0.360943151397873,-0.0879765498725935,0.498152820104387,0.0144869362852196,0.0227727508910433,0.0703293266867484,0.122218460819597,0.0187193579790059,0.0748155705901153,0.0152662509264448,0.103280661825357,0.0206707911334189,0.0469680672449185,0.191924771634855,0.228988494378382,0.149284359106596,0.182405495183226,0.168729938717137,0.140576373162955,0.0233767308162502,-0.0168972054823298,0.0853589958297434,0.139848545625618,0.130653000540023,0.160362605538622,0.0183412399191695,0.0386172844377699,0.0397146082698624,-0.0763070706516341,0.109139713999277,0.0401905250181448,0.0417260085337083,-0.00164638709283641,0.0450684688817151,0.210186651836142,0.172889266385625,0.0107595839724166,-0.0122336364002499,0.243749063648732,-0.191139142639362,0.0415737316882645,0.645591569470622,0.0723188504245408,0.0655587893442501,0.165537977983933,0.076061580072536,0.0459018579916069,0.163427686059758,0.0848564155079657,0.161876892248929,0.0480261185106972,0.129986545084288,0.0810178910786705,0.0425456996910303,0.00633962414398873,0.106488956655736,-0.0125032790767612,0.117288461733186,0.0975307449516248,0.108926781531133,0.0707360223840162,0.0511170568188523,0.0395124920832913,0.150781224830252,0.072208743862719,-0.000487524603530823,0.068196941741002,0.154095321580211,0.0209209720173831,-0.186014274697128,0.0890394866754344,-0.0361571466437379,-0.174253205533414,0.189591478535594,0.0787740685384461,0.0446371450341465,0.105081821801222,0.101537675359982,0.00407878963326747,0.296111292493487,0.018958238612646,0.105161645767796,0.0934349399507468,0.0227524784516293,0.0653887480138476,0.0330984674804971,-0.0211509613147106,0.0279300759891456,0.164073522663505,-0.138482275055307,0.0646316060329462,0.000588326919082614,-0.00641133074980723,0.588441672516655,0.0613093185601324,0.150209350768519,0.203661530442687,0.0185656506354017,0.0909420458304519,0.0554310697838179,-0.0338005606173955,0.0100848603774595,0.0884343317130743,-0.0358678508827478,0.205037873931704,0.233405231846224,0.139695436536765,0.138120675204841,0.106444534177716,0.191313975218266,0.0515640371071081,0.049703393464885,0.0680561867795258,0.0795566732806106,0.194462229511758,-0.567747199240083,0.0673027101343094,0.00886872619323937,0.0265214970977995,0.118434935841627,-0.100333009083752,-0.00864564340207863,-0.0220594895924997,-0.0352498067357213,0.153807194686939,0.0292899666335785,0.111214517256363,0.159782493028875,0.0704422381798033,0.00803271581598383,0.155941754311095,0.0682904781178035,0.125758201498529,-0.01900474135033,0.222431401143217,0.182708441543612,0.0370496948559832,-0.00168492976549276,0.105909097911778,0.0578608542407222,0.116211390515319,0.0546671275950352,0.177385486984977,0.0395184869196772,-0.0244872936812863,0.0132203404633814,0.016505375662768,0.0985886535209214,-0.0507500350830676,0.0574163636788137,0.209007346504408,0.0119420747701743,0.000632874517476114,0.0814092140072102,0.0675327596085879,null,0.084018594029945,0.0939404149402457,0.203389649750232,0.10032927457408,-0.0296869758301049,0.102360881231629,-0.135351475353937,0.104981771985735,-0.193195713778077,0.0710595324957131,0.0852327334750742,0.0370470999407731,0.0768843660456694,0.149762439177948,0.0145142791435828,0.141563067169703,0.135804792562449,0.00944509849411724,0.0864486570297521,0.130262613763116,0.170540177982741,0.116339500505618,0.0119734861240268,0.1762347163116,0.199385948252128,0.0168968601762414,-0.0979814872537552,0.0940806435569895,-0.0378904394710405,0.112216094230866,0.0968230442560816,0.0241597857374953,0.0144663282329371,0.0770530209200049,0.114441564302024,0.00341130648474301,0.106980719790308,-0.107954647242786,0.0194759208317426,0.013607658029196,0.0293652486084558,0.0849387978426582,0.159250697526554,0.12976541104889,-0.000616952580689252,0.0993803203919405,0.0759402410975187,-0.132480600034214,-0.012090886151479,0.0308945247377912,0.100859156652665,0.151510487448216,0.372213962959476,0.140779087326243,0.0425790368667508,0.0412105079007395,-0.0284180434555303,0.0921877119262692,-0.0227170673553849,0.0760148081018038,0.0166416747605973,-0.0188360994986799,-0.175477975651671,0.123270165460188,0.340985896856643,0.165366731724757,0.0681008599419041,0.0566424000508248,-0.0466169216621611,0.0584427043361578,0.095058562270307],"y":[11.2411167416747,11.4360444206343,11.8684998034649,11.5119249646366,12.1001564199386,12.0552497557956,11.4957793061353,12.2505678854167,11.45741275504,11.5268283701392,11.9322934782474,12.4008167223227,12.314478519374,11.45741275504,11.9170563500653,12.0598901353521,12.0033442789586,12.1463226411244,12.4825673723414,11.7829526021833,11.645706576204,12.0668105781967,12.3318238508357,12.5991277335617,11.7472067606949,12.8989697948349,11.8451027773086,11.6199845372636,11.6082356447746,11.3277999808435,12.5724503649303,12.6388286138742,11.987916635727,11.4658338574364,11.8122890421958,11.792827350103,11.8747869355963,11.6885580336134,12.1264881661873,12.8703058159255,12.7674012514693,11.7472067606949,12.5375323403278,13.0902533234861,11.1704351560235,11.8899910985567,11.6000201718212,11.80335376309,12.3579349948394,11.7424486232485,12.3135808532455,11.6724900346416,12.5584885325485,11.9904011090547,11.7752897294377,11.8041014266763,11.4741846366538,12.1232343672212,12.0106658491876,12.5102430354868,11.7852400602909,11.9984332807519,12.428816116823,12.5194224647305,11.9381932003746,11.6342577501378,11.7304532774988,11.9063179918441,12.2690474446916,11.7035458245789,12.2666972673466,11.8858673813728,11.7920712063997,11.7142323216753,11.744830521953,11.9891596439666,11.4772982873271,12.4411447677097,11.588032937457,11.8768738928755,11.681824001432,11.2185544043677,11.460578984598,11.6699292137799,11.7464153083386,11.5655179150894,11.3850920934603,12.1399328430256,12.4086052429403,11.9090134112658,12.0002777325506,11.4845259904485,12.1965272326866,11.7860013850326,11.8422292121128,12.0968156595932,11.8851784388723,12.2346601023821,11.7093142789756,11.7288429711927,11.3385720778255,11.4637352207795,11.5833839286188,12.3050125933851,11.6091443227108,12.197031900878,11.8692003288876,11.8262752841706,11.6091443227108,11.906992528126,12.4478416609675,11.7158663089669,11.4467856624657,11.4876076569859,11.8371805176529,12.4020505287716,11.3805362769245,11.60276616897,12.5017228876311,11.4647850896423,12.0827744291857,12.0500034598803,11.9276806199855,11.5405406320032,11.7134143257196,12.2520015774186,11.879649744762,11.8189384941067,12.197031900878,11.9492430365612,11.818201845823,11.6483301019764,11.7920712063997,11.3169105810443,11.805595078933,12.2520015774186,12.3072745260391,11.9518253491646,12.1420673155543,12.4316133214441,11.5917366453945,11.6604830293278,11.5502212497139,11.7142323216753,11.6091443227108,11.8108053623985,11.4008759611616,11.8656927840779,11.8817265887068,11.8600549960654,12.0100577616042,11.9511803959014,11.8100626961928,11.6935789646635,11.5935833679877,12.1547793511426,11.7519423654407,11.8130300574206,11.7256145583806,11.6421978006744,11.3181263866652,11.4284563083438,11.4435753868354,11.8536742583587,11.8393473657379,11.9511803959014,11.9640010843304,11.5721373246021,11.5395673959167,12.3863086958331,11.8649897963513,11.610052175701,11.8810347865346,11.7798944958245,11.5258416902368,12.0968156595932,11.8479681087818,12.0878520141427,11.9243726447559,11.5028751291167,11.7636841833174,12.5371733383495,12.056992422516,11.4478534682265,11.9150516718129,11.9042916486989,11.9362304912067,11.9434083360537,11.5297825820367,11.8684998034649,11.7142323216753,12.04296530766,11.4626842485335,12.1199699464768,11.8593480324446,11.4762614805986,11.8670972786908,11.645706576204,12.6014874177848,12.2954562066649,12.5120856746667,11.8152498141589,12.0082312770782,11.6226763289293,11.3828167796232,11.1533892887505,12.5317727851695,11.7737500832521,12.5528487572897,12.5131896306206,11.6767435501996,11.6045926534961,12.2035695153121,12.3900594816432,12.3278477024561,11.6369114447512,12.6813747132271,11.5079129231467,12.0161220615717,11.689396608086,11.65355659471,11.6190856607986,12.4916274569658,11.4262776582446,11.6448305358502,12.0167264737993,13.3076804431781,12.8325456928221,12.0124878964575,12.5117174183561,12.0476629087825,13.0123252721954,11.814510442591,12.4829465192654,11.9143825516809,12.7510097989249,11.1228414589004,12.1547793511426,11.659619844121,12.4240026297915,11.8407893270548,12.3140297870353,11.8436670268825,11.5038847203181,13.2932868892459,12.1848490090785,12.0901004692778,11.5189075366478,11.9678154564059,11.6868787720937,12.3745487955021,12.3783438664706,11.1732480974001,11.6369114447512,12.2194823324401,11.7360690162844,11.4489201349943,12.372857463175,12.53789121347,12.2718603860682,12.3575053492904,12.5923549342216,12.3260754379249,11.8357333393974,12.173032791452,12.0535040468856,12.1558314290934,11.8649897963513,12.0057907633592,12.5054362227558,12.6710637329524,12.281180118017,12.758519943987,11.9569700550459,12.0376539939052,11.7084922485142,11.7775947631129,11.5069073926447,11.6868787720937,12.8431784352065,11.6036798282387,12.0598901353521,12.3917219924168,11.57307938779,11.9524698867313,12.2115575757607,13.3192450855296,12.112860263808,12.330941627576,11.3277999808435,11.6526874073454,13.1546369379546,11.8299235917561,13.4073919323905,11.3884953865921,13.4595496447592,11.6944133410156,13.1887127579459,13.4229123155629,12.5696735495396,13.2436956625719,12.0179342034147,11.671637156125,12.7693958382539,12.2145367239423,11.9049675527463,11.4647850896423,11.6009363422929,11.4446466242169,11.8451027773086,11.659619844121,11.6226763289293,12.0951410848229,11.6430761494353,12.2685778508816,11.7312574592872,11.6109592052416,12.0269459796327,12.7798730684576,11.4489201349943,11.6145791186967,12.0511716843122,12.1313490993342,11.3456895455943,11.3337987990728,11.7667921889273,11.6217798698823,12.6497964657554,12.1904512646272,11.6673618182746,11.7965995160245,11.6395581159036,11.4552963521336,11.65355659471,12.9731670710422,11.4064532204597,12.0340973807904,12.3613655299362,12.2899541295109,11.4845259904485,11.762905670238,12.9553638367082,11.6613454700885,11.8189384941067,11.3385720778255,12.2567657598457,11.3290026268093,11.6217798698823,11.3456895455943,11.6448305358502,12.1822921168648,12.3484398868171,11.8515382660906,12.5602444592508,11.8719975335087,12.021548665181,11.4998402254216,12.4904994252613,11.792827350103],"text":["pop_growth: 0.0662555899<br />loghome_value: 11.24112<br />Metro Area: Abilene, TX Metro Area<br />pop09E: 159110","pop_growth: -0.0897005014<br />loghome_value: 11.43604<br />Metro Area: Aguadilla-Isabela-San Sebasti?n, PR Metro Area<br />pop09E: 336418","pop_growth: 0.0060256071<br />loghome_value: 11.86850<br />Metro Area: Akron, OH Metro Area<br />pop09E: 700222","pop_growth: -0.0670353850<br />loghome_value: 11.51192<br />Metro Area: Albany, GA Metro Area<br />pop09E: 163716","pop_growth: 0.0326916995<br />loghome_value: 12.10016<br />Metro Area: Albany-Schenectady-Troy, NY Metro Area<br />pop09E: 852162","pop_growth: 0.0906198301<br />loghome_value: 12.05525<br />Metro Area: Albuquerque, NM Metro Area<br />pop09E: 831173","pop_growth: 0.0129560652<br />loghome_value: 11.49578<br />Metro Area: Alexandria, LA Metro Area<br />pop09E: 151913","pop_growth: 0.0384788498<br />loghome_value: 12.25057<br />Metro Area: Allentown-Bethlehem-Easton, PA-NJ Metro Area<br />pop09E: 803110","pop_growth: -0.0171483552<br />loghome_value: 11.45741<br />Metro Area: Altoona, PA Metro Area<br />pop09E: 125984","pop_growth: 0.0853644346<br />loghome_value: 11.52683<br />Metro Area: Amarillo, TX Metro Area<br />pop09E: 241859","pop_growth: 0.1338468654<br />loghome_value: 11.93229<br />Metro Area: Ames, IA Metro Area<br />pop09E: 84780","pop_growth: 0.0974126146<br />loghome_value: 12.40082<br />Metro Area: Anchorage, AK Metro Area<br />pop09E: 362488","pop_growth: 0.0560677643<br />loghome_value: 12.31448<br />Metro Area: Ann Arbor, MI Metro Area<br />pop09E: 346007","pop_growth: 0.0186704946<br />loghome_value: 11.45741<br />Metro Area: Anniston-Oxford, AL Metro Area<br />pop09E: 112969","pop_growth: 0.0731564011<br />loghome_value: 11.91706<br />Metro Area: Appleton, WI Metro Area<br />pop09E: 218014","pop_growth: 0.1102603450<br />loghome_value: 12.05989<br />Metro Area: Asheville, NC Metro Area<br />pop09E: 402964","pop_growth: 0.0976870543<br />loghome_value: 12.00334<br />Metro Area: Athens-Clarke County, GA Metro Area<br />pop09E: 186196","pop_growth: 0.0981812766<br />loghome_value: 12.14632<br />Metro Area: Atlanta-Sandy Springs-Marietta, GA Metro Area<br />pop09E: 5238994","pop_growth: -0.0054850617<br />loghome_value: 12.48257<br />Metro Area: Atlantic City-Hammonton, NJ Metro Area<br />pop09E: 270016","pop_growth: 0.1980401984<br />loghome_value: 11.78295<br />Metro Area: Auburn-Opelika, AL Metro Area<br />pop09E: 130669","pop_growth: 0.1170746798<br />loghome_value: 11.64571<br />Metro Area: Augusta-Richmond County, GA-SC Metro Area<br />pop09E: 528641","pop_growth: 0.2585529945<br />loghome_value: 12.06681<br />Metro Area: Austin-Round Rock, TX Metro Area<br />pop09E: 1589393","pop_growth: 0.1228702527<br />loghome_value: 12.33182<br />Metro Area: Bakersfield, CA Metro Area<br />pop09E: 780953","pop_growth: 0.0451321890<br />loghome_value: 12.59913<br />Metro Area: Baltimore-Towson, MD Metro Area<br />pop09E: 2669987","pop_growth: 0.0216295581<br />loghome_value: 11.74721<br />Metro Area: Bangor, ME Metro Area<br />pop09E: 148501","pop_growth: -0.0409803422<br />loghome_value: 12.89897<br />Metro Area: Barnstable Town, MA Metro Area<br />pop09E: 222629","pop_growth: 0.0790252161<br />loghome_value: 11.84510<br />Metro Area: Baton Rouge, LA Metro Area<br />pop09E: 766603","pop_growth: -0.0177046652<br />loghome_value: 11.61998<br />Metro Area: Battle Creek, MI Metro Area<br />pop09E: 136875","pop_growth: -0.0281533808<br />loghome_value: 11.60824<br />Metro Area: Bay City, MI Metro Area<br />pop09E: 107778","pop_growth: 0.0831602588<br />loghome_value: 11.32780<br />Metro Area: Beaumont-Port Arthur, TX Metro Area<br />pop09E: 377001","pop_growth: 0.1169312778<br />loghome_value: 12.57245<br />Metro Area: Bellingham, WA Metro Area<br />pop09E: 192886","pop_growth: 0.1734219492<br />loghome_value: 12.63883<br />Metro Area: Bend, OR Metro Area<br />pop09E: 151879","pop_growth: 0.1185928628<br />loghome_value: 11.98792<br />Metro Area: Billings, MT Metro Area<br />pop09E: 150177","pop_growth: -0.0087072119<br />loghome_value: 11.46583<br />Metro Area: Binghamton, NY Metro Area<br />pop09E: 245576","pop_growth: 0.0308451921<br />loghome_value: 11.81229<br />Metro Area: Birmingham-Hoover, AL Metro Area<br />pop09E: 1112213","pop_growth: 0.2378628218<br />loghome_value: 11.79283<br />Metro Area: Bismarck, ND Metro Area<br />pop09E: 102899","pop_growth: 0.1478890533<br />loghome_value: 11.87479<br />Metro Area: Blacksburg-Christiansburg-Radford, VA Metro Area<br />pop09E: 157274","pop_growth: -0.0954845682<br />loghome_value: 11.68856<br />Metro Area: Bloomington, IN Metro Area<br />pop09E: 182941","pop_growth: 0.1786370314<br />loghome_value: 12.12649<br />Metro Area: Boise City-Nampa, ID Metro Area<br />pop09E: 580428","pop_growth: 0.0638880454<br />loghome_value: 12.87031<br />Metro Area: Boston-Cambridge-Quincy, MA-NH Metro Area<br />pop09E: 4513934","pop_growth: 0.0827845249<br />loghome_value: 12.76740<br />Metro Area: Boulder, CO Metro Area<br />pop09E: 295524","pop_growth: 0.3906727965<br />loghome_value: 11.74721<br />Metro Area: Bowling Green, KY Metro Area<br />pop09E: 116435","pop_growth: 0.0944247732<br />loghome_value: 12.53753<br />Metro Area: Bremerton-Silverdale, WA Metro Area<br />pop09E: 238825","pop_growth: 0.0560839887<br />loghome_value: 13.09025<br />Metro Area: Bridgeport-Stamford-Norwalk, CT Metro Area<br />pop09E: 892843","pop_growth: 0.0959313567<br />loghome_value: 11.17044<br />Metro Area: Brownsville-Harlingen, TX Metro Area<br />pop09E: 383171","pop_growth: 0.1419541339<br />loghome_value: 11.88999<br />Metro Area: Brunswick, GA Metro Area<br />pop09E: 101217","pop_growth: 0.0024394108<br />loghome_value: 11.60002<br />Metro Area: Buffalo-Niagara Falls, NY Metro Area<br />pop09E: 1128813","pop_growth: 0.1036279821<br />loghome_value: 11.80335<br />Metro Area: Burlington, NC Metro Area<br />pop09E: 144769","pop_growth: 0.0550654884<br />loghome_value: 12.35793<br />Metro Area: Burlington-South Burlington, VT Metro Area<br />pop09E: 206360","pop_growth: -0.0177126566<br />loghome_value: 11.74245<br />Metro Area: Canton-Massillon, OH Metro Area<br />pop09E: 408220","pop_growth: 0.2253500276<br />loghome_value: 12.31358<br />Metro Area: Cape Coral-Fort Myers, FL Metro Area<br />pop09E: 573676","pop_growth: 0.0444695445<br />loghome_value: 11.67249<br />Metro Area: Cape Girardeau-Jackson, MO-IL Metro Area<br />pop09E: 92912","pop_growth: -0.0144904977<br />loghome_value: 12.55849<br />Metro Area: Carson City, NV Metro Area<br />pop09E: 55262","pop_growth: 0.1155014945<br />loghome_value: 11.99040<br />Metro Area: Casper, WY Metro Area<br />pop09E: 71817","pop_growth: 0.0629389464<br />loghome_value: 11.77529<br />Metro Area: Cedar Rapids, IA Metro Area<br />pop09E: 251948","pop_growth: 0.0722197359<br />loghome_value: 11.80410<br />Metro Area: Champaign-Urbana, IL Metro Area<br />pop09E: 222602","pop_growth: -0.3349597707<br />loghome_value: 11.47418<br />Metro Area: Charleston, WV Metro Area<br />pop09E: 303777","pop_growth: 0.1842545477<br />loghome_value: 12.12323<br />Metro Area: Charleston-North Charleston-Summerville, SC Metro Area<br />pop09E: 631484","pop_growth: 0.4100201215<br />loghome_value: 12.01067<br />Metro Area: Charlotte-Gastonia-Concord, NC-SC Metro Area<br />pop09E: 1641257","pop_growth: 0.1818322978<br />loghome_value: 12.51024<br />Metro Area: Charlottesville, VA Metro Area<br />pop09E: 192515","pop_growth: 0.0700067639<br />loghome_value: 11.78524<br />Metro Area: Chattanooga, TN-GA Metro Area<br />pop09E: 514718","pop_growth: 0.1171537042<br />loghome_value: 11.99843<br />Metro Area: Cheyenne, WY Metro Area<br />pop09E: 86892","pop_growth: 0.0078546611<br />loghome_value: 12.42882<br />Metro Area: Chicago-Naperville-Joliet, IL-IN-WI Metro Area<br />pop09E: 9461816","pop_growth: 0.0411661030<br />loghome_value: 12.51942<br />Metro Area: Chico, CA Metro Area<br />pop09E: 217917","pop_growth: 0.0130078238<br />loghome_value: 11.93819<br />Metro Area: Cincinnati-Middletown, OH-KY-IN Metro Area<br />pop09E: 2140796","pop_growth: 0.0869541978<br />loghome_value: 11.63426<br />Metro Area: Clarksville, TN-KY Metro Area<br />pop09E: 259426","pop_growth: 0.0897880760<br />loghome_value: 11.73045<br />Metro Area: Cleveland, TN Metro Area<br />pop09E: 110919","pop_growth: -0.0192412147<br />loghome_value: 11.90632<br />Metro Area: Cleveland-Elyria-Mentor, OH Metro Area<br />pop09E: 2101821","pop_growth: 0.1405750719<br />loghome_value: 12.26905<br />Metro Area: Coeur d'Alene, ID Metro Area<br />pop09E: 133461","pop_growth: 0.2197568392<br />loghome_value: 11.70355<br />Metro Area: College Station-Bryan, TX Metro Area<br />pop09E: 203846","pop_growth: 0.1582765552<br />loghome_value: 12.26670<br />Metro Area: Colorado Springs, CO Metro Area<br />pop09E: 608000","pop_growth: 0.0876940140<br />loghome_value: 11.88587<br />Metro Area: Columbia, MO Metro Area<br />pop09E: 161695","pop_growth: 0.1275847745<br />loghome_value: 11.79207<br />Metro Area: Columbia, SC Metro Area<br />pop09E: 718843","pop_growth: 0.0626381905<br />loghome_value: 11.71423<br />Metro Area: Columbus, GA-AL Metro Area<br />pop09E: 289040","pop_growth: 0.0921878081<br />loghome_value: 11.74483<br />Metro Area: Columbus, IN Metro Area<br />pop09E: 74681","pop_growth: 0.1553404946<br />loghome_value: 11.98916<br />Metro Area: Columbus, OH Metro Area<br />pop09E: 1758531","pop_growth: 0.0918705632<br />loghome_value: 11.47730<br />Metro Area: Corpus Christi, TX Metro Area<br />pop09E: 412594","pop_growth: 0.1015929628<br />loghome_value: 12.44114<br />Metro Area: Corvallis, OR Metro Area<br />pop09E: 81107","pop_growth: -0.0030480928<br />loghome_value: 11.58803<br />Metro Area: Cumberland, MD-WV Metro Area<br />pop09E: 99558","pop_growth: 0.1661806647<br />loghome_value: 11.87687<br />Metro Area: Dallas-Fort Worth-Arlington, TX Metro Area<br />pop09E: 6144234","pop_growth: 0.0766322387<br />loghome_value: 11.68182<br />Metro Area: Dalton, GA Metro Area<br />pop09E: 132827","pop_growth: -0.0316219478<br />loghome_value: 11.21855<br />Metro Area: Danville, IL Metro Area<br />pop09E: 80926","pop_growth: -0.0281498795<br />loghome_value: 11.46058<br />Metro Area: Danville, VA Metro Area<br />pop09E: 106134","pop_growth: 0.0187070216<br />loghome_value: 11.66993<br />Metro Area: Davenport-Moline-Rock Island, IA-IL Metro Area<br />pop09E: 375627","pop_growth: -0.0447259813<br />loghome_value: 11.74642<br />Metro Area: Dayton, OH Metro Area<br />pop09E: 839359","pop_growth: 0.0199088755<br />loghome_value: 11.56552<br />Metro Area: Decatur, AL Metro Area<br />pop09E: 149291","pop_growth: -0.0209962935<br />loghome_value: 11.38509<br />Metro Area: Decatur, IL Metro Area<br />pop09E: 108772","pop_growth: 0.2498234434<br />loghome_value: 12.13993<br />Metro Area: Deltona-Daytona Beach-Ormond Beach, FL Metro Area<br />pop09E: 494449","pop_growth: 0.1508849268<br />loghome_value: 12.40861<br />Metro Area: Denver-Aurora-Broomfield, CO Metro Area<br />pop09E: 2451038","pop_growth: 0.1542607982<br />loghome_value: 11.90901<br />Metro Area: Des Moines-West Des Moines, IA Metro Area<br />pop09E: 543541","pop_growth: -0.0308743369<br />loghome_value: 12.00028<br />Metro Area: Detroit-Warren-Livonia, MI Metro Area<br />pop09E: 4452548","pop_growth: 0.0591325816<br />loghome_value: 11.48453<br />Metro Area: Dothan, AL Metro Area<br />pop09E: 139471","pop_growth: 0.1442922147<br />loghome_value: 12.19653<br />Metro Area: Dover, DE Metro Area<br />pop09E: 151332","pop_growth: 0.0503792031<br />loghome_value: 11.78600<br />Metro Area: Dubuque, IA Metro Area<br />pop09E: 92046","pop_growth: 0.0157967130<br />loghome_value: 11.84223<br />Metro Area: Duluth, MN-WI Metro Area<br />pop09E: 274649","pop_growth: 0.1524028514<br />loghome_value: 12.09682<br />Metro Area: Durham-Chapel Hill, NC Metro Area<br />pop09E: 479544","pop_growth: 0.0576351143<br />loghome_value: 11.88518<br />Metro Area: Eau Claire, WI Metro Area<br />pop09E: 157294","pop_growth: 0.1187698388<br />loghome_value: 12.23466<br />Metro Area: El Centro, CA Metro Area<br />pop09E: 160034","pop_growth: 0.2987294982<br />loghome_value: 11.70931<br />Metro Area: Elizabethtown, KY Metro Area<br />pop09E: 111692","pop_growth: 0.0286627087<br />loghome_value: 11.72884<br />Metro Area: Elkhart-Goshen, IN Metro Area<br />pop09E: 197851","pop_growth: -0.0278452272<br />loghome_value: 11.33857<br />Metro Area: Elmira, NY Metro Area<br />pop09E: 88161","pop_growth: 0.1432686396<br />loghome_value: 11.46374<br />Metro Area: El Paso, TX Metro Area<br />pop09E: 729396","pop_growth: -0.0134932665<br />loghome_value: 11.58338<br />Metro Area: Erie, PA Metro Area<br />pop09E: 279721","pop_growth: 0.0704923450<br />loghome_value: 12.30501<br />Metro Area: Eugene-Springfield, OR Metro Area<br />pop09E: 343774","pop_growth: -0.1048651030<br />loghome_value: 11.60914<br />Metro Area: Evansville, IN-KY Metro Area<br />pop09E: 349790","pop_growth: 0.0286030411<br />loghome_value: 12.19703<br />Metro Area: Fairbanks, AK Metro Area<br />pop09E: 96843","pop_growth: 0.2069122771<br />loghome_value: 11.86920<br />Metro Area: Fargo, ND-MN Metro Area<br />pop09E: 192705","pop_growth: 0.0398972591<br />loghome_value: 11.82628<br />Metro Area: Farmington, NM Metro Area<br />pop09E: 122470","pop_growth: 0.0912865735<br />loghome_value: 11.60914<br />Metro Area: Fayetteville, NC Metro Area<br />pop09E: 351726","pop_growth: 0.1755619345<br />loghome_value: 11.90699<br />Metro Area: Fayetteville-Springdale-Rogers, AR-MO Metro Area<br />pop09E: 441652","pop_growth: 0.0965504560<br />loghome_value: 12.44784<br />Metro Area: Flagstaff, AZ Metro Area<br />pop09E: 127312","pop_growth: -0.0554934602<br />loghome_value: 11.71587<br />Metro Area: Flint, MI Metro Area<br />pop09E: 432720","pop_growth: 0.0340500061<br />loghome_value: 11.44679<br />Metro Area: Florence, SC Metro Area<br />pop09E: 198924","pop_growth: 0.0274609227<br />loghome_value: 11.48761<br />Metro Area: Florence-Muscle Shoals, AL Metro Area<br />pop09E: 143096","pop_growth: 0.0295482467<br />loghome_value: 11.83718<br />Metro Area: Fond du Lac, WI Metro Area<br />pop09E: 99336","pop_growth: 0.1641165557<br />loghome_value: 12.40205<br />Metro Area: Fort Collins-Loveland, CO Metro Area<br />pop09E: 286978","pop_growth: -0.0255144451<br />loghome_value: 11.38054<br />Metro Area: Fort Smith, AR-OK Metro Area<br />pop09E: 288468","pop_growth: 0.0541297794<br />loghome_value: 11.60277<br />Metro Area: Fort Wayne, IN Metro Area<br />pop09E: 408870","pop_growth: 0.0935787811<br />loghome_value: 12.50172<br />Metro Area: Fresno, CA Metro Area<br />pop09E: 890750","pop_growth: -0.0020476597<br />loghome_value: 11.46479<br />Metro Area: Gadsden, AL Metro Area<br />pop09E: 103150","pop_growth: 0.0932674824<br />loghome_value: 12.08277<br />Metro Area: Gainesville, FL Metro Area<br />pop09E: 255761","pop_growth: 0.0979033402<br />loghome_value: 12.05000<br />Metro Area: Gainesville, GA Metro Area<br />pop09E: 177685","pop_growth: -0.0150943594<br />loghome_value: 11.92768<br />Metro Area: Glens Falls, NY Metro Area<br />pop09E: 128229","pop_growth: 0.0903467916<br />loghome_value: 11.54054<br />Metro Area: Goldsboro, NC Metro Area<br />pop09E: 113290","pop_growth: 0.0474350807<br />loghome_value: 11.71341<br />Metro Area: Grand Forks, ND-MN Metro Area<br />pop09E: 97266","pop_growth: 0.0842454717<br />loghome_value: 12.25200<br />Metro Area: Grand Junction, CO Metro Area<br />pop09E: 137879","pop_growth: 0.3061331136<br />loghome_value: 11.87965<br />Metro Area: Grand Rapids-Wyoming, MI Metro Area<br />pop09E: 773427","pop_growth: -0.0020286214<br />loghome_value: 11.81894<br />Metro Area: Great Falls, MT Metro Area<br />pop09E: 81912","pop_growth: 0.2016786929<br />loghome_value: 12.19703<br />Metro Area: Greeley, CO Metro Area<br />pop09E: 241221","pop_growth: 0.0554764167<br />loghome_value: 11.94924<br />Metro Area: Green Bay, WI Metro Area<br />pop09E: 300557","pop_growth: 0.0858146236<br />loghome_value: 11.81820<br />Metro Area: Greensboro-High Point, NC Metro Area<br />pop09E: 695491","pop_growth: 0.0288205704<br />loghome_value: 11.64833<br />Metro Area: Greenville, NC Metro Area<br />pop09E: 172333","pop_growth: 0.3609431514<br />loghome_value: 11.79207<br />Metro Area: Greenville-Mauldin-Easley, SC Metro Area<br />pop09E: 616062","pop_growth: -0.0879765499<br />loghome_value: 11.31691<br />Metro Area: Guayama, PR Metro Area<br />pop09E: 84246","pop_growth: 0.4981528201<br />loghome_value: 11.80560<br />Metro Area: Gulfport-Biloxi, MS Metro Area<br />pop09E: 237770","pop_growth: 0.0144869363<br />loghome_value: 12.25200<br />Metro Area: Hagerstown-Martinsburg, MD-WV Metro Area<br />pop09E: 259519","pop_growth: 0.0227727509<br />loghome_value: 12.30727<br />Metro Area: Hanford-Corcoran, CA Metro Area<br />pop09E: 146696","pop_growth: 0.0703293267<br />loghome_value: 11.95183<br />Metro Area: Harrisburg-Carlisle, PA Metro Area<br />pop09E: 529306","pop_growth: 0.1222184608<br />loghome_value: 12.14207<br />Metro Area: Harrisonburg, VA Metro Area<br />pop09E: 117553","pop_growth: 0.0187193580<br />loghome_value: 12.43161<br />Metro Area: Hartford-West Hartford-East Hartford, CT Metro Area<br />pop09E: 1186939","pop_growth: 0.0748155706<br />loghome_value: 11.59174<br />Metro Area: Hattiesburg, MS Metro Area<br />pop09E: 138044","pop_growth: 0.0152662509<br />loghome_value: 11.66048<br />Metro Area: Hickory-Lenoir-Morganton, NC Metro Area<br />pop09E: 359804","pop_growth: 0.1032806618<br />loghome_value: 11.55022<br />Metro Area: Hinesville-Fort Stewart, GA Metro Area<br />pop09E: 72388","pop_growth: 0.0206707911<br />loghome_value: 11.71423<br />Metro Area: Hot Springs, AR Metro Area<br />pop09E: 96285","pop_growth: 0.0469680672<br />loghome_value: 11.60914<br />Metro Area: Houma-Bayou Cane-Thibodaux, LA Metro Area<br />pop09E: 201129","pop_growth: 0.1919247716<br />loghome_value: 11.81081<br />Metro Area: Houston-Sugar Land-Baytown, TX Metro Area<br />pop09E: 5595262","pop_growth: 0.2289884944<br />loghome_value: 11.40088<br />Metro Area: Huntington-Ashland, WV-KY-OH Metro Area<br />pop09E: 284917","pop_growth: 0.1492843591<br />loghome_value: 11.86569<br />Metro Area: Huntsville, AL Metro Area<br />pop09E: 388123","pop_growth: 0.1824054952<br />loghome_value: 11.88173<br />Metro Area: Idaho Falls, ID Metro Area<br />pop09E: 119130","pop_growth: 0.1687299387<br />loghome_value: 11.86005<br />Metro Area: Indianapolis-Carmel, IN Metro Area<br />pop09E: 1695807","pop_growth: 0.1405763732<br />loghome_value: 12.01006<br />Metro Area: Iowa City, IA Metro Area<br />pop09E: 146962","pop_growth: 0.0233767308<br />loghome_value: 11.95118<br />Metro Area: Ithaca, NY Metro Area<br />pop09E: 100583","pop_growth: -0.0168972055<br />loghome_value: 11.81006<br />Metro Area: Jackson, MI Metro Area<br />pop09E: 161621","pop_growth: 0.0853589958<br />loghome_value: 11.69358<br />Metro Area: Jackson, MS Metro Area<br />pop09E: 532803","pop_growth: 0.1398485456<br />loghome_value: 11.59358<br />Metro Area: Jackson, TN Metro Area<br />pop09E: 112452","pop_growth: 0.1306530005<br />loghome_value: 12.15478<br />Metro Area: Jacksonville, FL Metro Area<br />pop09E: 1294684","pop_growth: 0.1603626055<br />loghome_value: 11.75194<br />Metro Area: Jacksonville, NC Metro Area<br />pop09E: 165181","pop_growth: 0.0183412399<br />loghome_value: 11.81303<br />Metro Area: Janesville, WI Metro Area<br />pop09E: 158829","pop_growth: 0.0386172844<br />loghome_value: 11.72561<br />Metro Area: Jefferson City, MO Metro Area<br />pop09E: 145431","pop_growth: 0.0397146083<br />loghome_value: 11.64220<br />Metro Area: Johnson City, TN Metro Area<br />pop09E: 193391","pop_growth: -0.0763070707<br />loghome_value: 11.31813<br />Metro Area: Johnstown, PA Metro Area<br />pop09E: 145219","pop_growth: 0.1091397140<br />loghome_value: 11.42846<br />Metro Area: Jonesboro, AR Metro Area<br />pop09E: 116339","pop_growth: 0.0401905250<br />loghome_value: 11.44358<br />Metro Area: Joplin, MO Metro Area<br />pop09E: 170450","pop_growth: 0.0417260085<br />loghome_value: 11.85367<br />Metro Area: Kalamazoo-Portage, MI Metro Area<br />pop09E: 323079","pop_growth: -0.0016463871<br />loghome_value: 11.83935<br />Metro Area: Kankakee-Bradley, IL Metro Area<br />pop09E: 111244","pop_growth: 0.0450684689<br />loghome_value: 11.95118<br />Metro Area: Kansas City, MO-KS Metro Area<br />pop09E: 2013797","pop_growth: 0.2101866518<br />loghome_value: 11.96400<br />Metro Area: Kennewick-Pasco-Richland, WA Metro Area<br />pop09E: 230834","pop_growth: 0.1728892664<br />loghome_value: 11.57214<br />Metro Area: Killeen-Temple-Fort Hood, TX Metro Area<br />pop09E: 368682","pop_growth: 0.0107595840<br />loghome_value: 11.53957<br />Metro Area: Kingsport-Bristol-Bristol, TN-VA Metro Area<br />pop09E: 303115","pop_growth: -0.0122336364<br />loghome_value: 12.38631<br />Metro Area: Kingston, NY Metro Area<br />pop09E: 181510","pop_growth: 0.2437490636<br />loghome_value: 11.86499<br />Metro Area: Knoxville, TN Metro Area<br />pop09E: 680629","pop_growth: -0.1911391426<br />loghome_value: 11.61005<br />Metro Area: Kokomo, IN Metro Area<br />pop09E: 99740","pop_growth: 0.0415737317<br />loghome_value: 11.88103<br />Metro Area: La Crosse, WI-MN Metro Area<br />pop09E: 130954","pop_growth: 0.6455915695<br />loghome_value: 11.77989<br />Metro Area: Lafayette, LA Metro Area<br />pop09E: 256392","pop_growth: 0.0723188504<br />loghome_value: 11.52584<br />Metro Area: Lake Charles, LA Metro Area<br />pop09E: 192605","pop_growth: 0.0655587893<br />loghome_value: 12.09682<br />Metro Area: Lake Havasu City-Kingman, AZ Metro Area<br />pop09E: 192988","pop_growth: 0.1655379780<br />loghome_value: 11.84797<br />Metro Area: Lakeland-Winter Haven, FL Metro Area<br />pop09E: 566657","pop_growth: 0.0760615801<br />loghome_value: 12.08785<br />Metro Area: Lancaster, PA Metro Area<br />pop09E: 498918","pop_growth: 0.0459018580<br />loghome_value: 11.92437<br />Metro Area: Lansing-East Lansing, MI Metro Area<br />pop09E: 455232","pop_growth: 0.1634276861<br />loghome_value: 11.50288<br />Metro Area: Laredo, TX Metro Area<br />pop09E: 231035","pop_growth: 0.0848564155<br />loghome_value: 11.76368<br />Metro Area: Las Cruces, NM Metro Area<br />pop09E: 197819","pop_growth: 0.1618768922<br />loghome_value: 12.53717<br />Metro Area: Las Vegas-Paradise, NV Metro Area<br />pop09E: 1821507","pop_growth: 0.0480261185<br />loghome_value: 12.05699<br />Metro Area: Lawrence, KS Metro Area<br />pop09E: 113724","pop_growth: 0.1299865451<br />loghome_value: 11.44785<br />Metro Area: Lawton, OK Metro Area<br />pop09E: 112828","pop_growth: 0.0810178911<br />loghome_value: 11.91505<br />Metro Area: Lebanon, PA Metro Area<br />pop09E: 127882","pop_growth: 0.0425456997<br />loghome_value: 11.90429<br />Metro Area: Lewiston, ID-WA Metro Area<br />pop09E: 59889","pop_growth: 0.0063396241<br />loghome_value: 11.93623<br />Metro Area: Lewiston-Auburn, ME Metro Area<br />pop09E: 106765","pop_growth: 0.1064889567<br />loghome_value: 11.94341<br />Metro Area: Lexington-Fayette, KY Metro Area<br />pop09E: 455593","pop_growth: -0.0125032791<br />loghome_value: 11.52978<br />Metro Area: Lima, OH Metro Area<br />pop09E: 104946","pop_growth: 0.1172884617<br />loghome_value: 11.86850<br />Metro Area: Lincoln, NE Metro Area<br />pop09E: 291007","pop_growth: 0.0975307450<br />loghome_value: 11.71423<br />Metro Area: Little Rock-North Little Rock-Conway, AR Metro Area<br />pop09E: 666248","pop_growth: 0.1089267815<br />loghome_value: 12.04297<br />Metro Area: Logan, UT-ID Metro Area<br />pop09E: 121619","pop_growth: 0.0707360224<br />loghome_value: 11.46268<br />Metro Area: Longview, TX Metro Area<br />pop09E: 202980","pop_growth: 0.0511170568<br />loghome_value: 12.11997<br />Metro Area: Longview, WA Metro Area<br />pop09E: 99874","pop_growth: 0.0395124921<br />loghome_value: 11.85935<br />Metro Area: Louisville-Jefferson County, KY-IN Metro Area<br />pop09E: 1235476","pop_growth: 0.1507812248<br />loghome_value: 11.47626<br />Metro Area: Lubbock, TX Metro Area<br />pop09E: 269297","pop_growth: 0.0722087439<br />loghome_value: 11.86710<br />Metro Area: Lynchburg, VA Metro Area<br />pop09E: 242509","pop_growth: -0.0004875246<br />loghome_value: 11.64571<br />Metro Area: Macon, GA Metro Area<br />pop09E: 229788","pop_growth: 0.0681969417<br />loghome_value: 12.60149<br />Metro Area: Madera-Chowchilla, CA Metro Area<br />pop09E: 144794","pop_growth: 0.1540953216<br />loghome_value: 12.29546<br />Metro Area: Madison, WI Metro Area<br />pop09E: 554843","pop_growth: 0.0209209720<br />loghome_value: 12.51209<br />Metro Area: Manchester-Nashua, NH Metro Area<br />pop09E: 402576","pop_growth: -0.1860142747<br />loghome_value: 11.81525<br />Metro Area: Manhattan, KS Metro Area<br />pop09E: 119048","pop_growth: 0.0890394867<br />loghome_value: 12.00823<br />Metro Area: Mankato-North Mankato, MN Metro Area<br />pop09E: 91577","pop_growth: -0.0361571466<br />loghome_value: 11.62268<br />Metro Area: Mansfield, OH Metro Area<br />pop09E: 125791","pop_growth: -0.1742532055<br />loghome_value: 11.38282<br />Metro Area: Mayag?ez, PR Metro Area<br />pop09E: 111221","pop_growth: 0.1895914785<br />loghome_value: 11.15339<br />Metro Area: McAllen-Edinburg-Mission, TX Metro Area<br />pop09E: 702697","pop_growth: 0.0787740685<br />loghome_value: 12.53177<br />Metro Area: Medford, OR Metro Area<br />pop09E: 198036","pop_growth: 0.0446371450<br />loghome_value: 11.77375<br />Metro Area: Memphis, TN-MS-AR Metro Area<br />pop09E: 1287231","pop_growth: 0.1050818218<br />loghome_value: 12.55285<br />Metro Area: Merced, CA Metro Area<br />pop09E: 242235","pop_growth: 0.1015376754<br />loghome_value: 12.51319<br />Metro Area: Miami-Fort Lauderdale-Pompano Beach, FL Metro Area<br />pop09E: 5484777","pop_growth: 0.0040787896<br />loghome_value: 11.67674<br />Metro Area: Michigan City-La Porte, IN Metro Area<br />pop09E: 110102","pop_growth: 0.2961112925<br />loghome_value: 11.60459<br />Metro Area: Midland, TX Metro Area<br />pop09E: 126287","pop_growth: 0.0189582386<br />loghome_value: 12.20357<br />Metro Area: Milwaukee-Waukesha-West Allis, WI Metro Area<br />pop09E: 1546312","pop_growth: 0.1051616458<br />loghome_value: 12.39006<br />Metro Area: Minneapolis-St. Paul-Bloomington, MN-WI Metro Area<br />pop09E: 3202412","pop_growth: 0.0934349400<br />loghome_value: 12.32785<br />Metro Area: Missoula, MT Metro Area<br />pop09E: 105637","pop_growth: 0.0227524785<br />loghome_value: 11.63691<br />Metro Area: Mobile, AL Metro Area<br />pop09E: 405331","pop_growth: 0.0653887480<br />loghome_value: 12.68137<br />Metro Area: Modesto, CA Metro Area<br />pop09E: 505165","pop_growth: 0.0330984675<br />loghome_value: 11.50791<br />Metro Area: Monroe, LA Metro Area<br />pop09E: 172737","pop_growth: -0.0211509613<br />loghome_value: 12.01612<br />Metro Area: Monroe, MI Metro Area<br />pop09E: 152899","pop_growth: 0.0279300760<br />loghome_value: 11.68940<br />Metro Area: Montgomery, AL Metro Area<br />pop09E: 363299","pop_growth: 0.1640735227<br />loghome_value: 11.65356<br />Metro Area: Morgantown, WV Metro Area<br />pop09E: 118042","pop_growth: -0.1384822751<br />loghome_value: 11.61909<br />Metro Area: Morristown, TN Metro Area<br />pop09E: 134363","pop_growth: 0.0646316060<br />loghome_value: 12.49163<br />Metro Area: Mount Vernon-Anacortes, WA Metro Area<br />pop09E: 116152","pop_growth: 0.0005883269<br />loghome_value: 11.42628<br />Metro Area: Muncie, IN Metro Area<br />pop09E: 115548","pop_growth: -0.0064113307<br />loghome_value: 11.64483<br />Metro Area: Muskegon-Norton Shores, MI Metro Area<br />pop09E: 174156","pop_growth: 0.5884416725<br />loghome_value: 12.01673<br />Metro Area: Myrtle Beach-North Myrtle Beach-Conway, SC Metro Area<br />pop09E: 248601","pop_growth: 0.0613093186<br />loghome_value: 13.30768<br />Metro Area: Napa, CA Metro Area<br />pop09E: 132173","pop_growth: 0.1502093508<br />loghome_value: 12.83255<br />Metro Area: Naples-Marco Island, FL Metro Area<br />pop09E: 313165","pop_growth: 0.2036615304<br />loghome_value: 12.01249<br />Metro Area: Nashville-Davidson--Murfreesboro--Franklin, TN Metro Area<br />pop09E: 1520649","pop_growth: 0.0185656506<br />loghome_value: 12.51172<br />Metro Area: New Haven-Milford, CT Metro Area<br />pop09E: 843532","pop_growth: 0.0909420458<br />loghome_value: 12.04766<br />Metro Area: New Orleans-Metairie-Kenner, LA Metro Area<br />pop09E: 1153788","pop_growth: 0.0554310698<br />loghome_value: 13.01233<br />Metro Area: New York-Northern New Jersey-Long Island, NY-NJ-PA Metro Area<br />pop09E: 18912644","pop_growth: -0.0338005606<br />loghome_value: 11.81451<br />Metro Area: Niles-Benton Harbor, MI Metro Area<br />pop09E: 160129","pop_growth: 0.0100848604<br />loghome_value: 12.48295<br />Metro Area: Norwich-New London, CT Metro Area<br />pop09E: 266183","pop_growth: 0.0884343317<br />loghome_value: 11.91438<br />Metro Area: Ocala, FL Metro Area<br />pop09E: 318886","pop_growth: -0.0358678509<br />loghome_value: 12.75101<br />Metro Area: Ocean City, NJ Metro Area<br />pop09E: 97127","pop_growth: 0.2050378739<br />loghome_value: 11.12284<br />Metro Area: Odessa, TX Metro Area<br />pop09E: 128988","pop_growth: 0.2334052318<br />loghome_value: 12.15478<br />Metro Area: Ogden-Clearfield, UT Metro Area<br />pop09E: 516864","pop_growth: 0.1396954365<br />loghome_value: 11.65962<br />Metro Area: Oklahoma City, OK Metro Area<br />pop09E: 1191174","pop_growth: 0.1381206752<br />loghome_value: 12.42400<br />Metro Area: Olympia, WA Metro Area<br />pop09E: 239248","pop_growth: 0.1064445342<br />loghome_value: 11.84079<br />Metro Area: Omaha-Council Bluffs, NE-IA Metro Area<br />pop09E: 829702","pop_growth: 0.1913139752<br />loghome_value: 12.31403<br />Metro Area: Orlando-Kissimmee, FL Metro Area<br />pop09E: 2023605","pop_growth: 0.0515640371<br />loghome_value: 11.84367<br />Metro Area: Oshkosh-Neenah, WI Metro Area<br />pop09E: 161386","pop_growth: 0.0497033935<br />loghome_value: 11.50388<br />Metro Area: Owensboro, KY Metro Area<br />pop09E: 112266","pop_growth: 0.0680561868<br />loghome_value: 13.29329<br />Metro Area: Oxnard-Thousand Oaks-Ventura, CA Metro Area<br />pop09E: 792313","pop_growth: 0.0795566733<br />loghome_value: 12.18485<br />Metro Area: Palm Bay-Melbourne-Titusville, FL Metro Area<br />pop09E: 532697","pop_growth: 0.1944622295<br />loghome_value: 12.09010<br />Metro Area: Panama City-Lynn Haven-Panama City Beach, FL Metro Area<br />pop09E: 163451","pop_growth: -0.5677471992<br />loghome_value: 11.51891<br />Metro Area: Parkersburg-Marietta-Vienna, WV-OH Metro Area<br />pop09E: 161173","pop_growth: 0.0673027101<br />loghome_value: 11.96782<br />Metro Area: Pensacola-Ferry Pass-Brent, FL Metro Area<br />pop09E: 450594","pop_growth: 0.0088687262<br />loghome_value: 11.68688<br />Metro Area: Peoria, IL Metro Area<br />pop09E: 371120","pop_growth: 0.0265214971<br />loghome_value: 12.37455<br />Metro Area: Philadelphia-Camden-Wilmington, PA-NJ-DE-MD Metro Area<br />pop09E: 5910593","pop_growth: 0.1184349358<br />loghome_value: 12.37834<br />Metro Area: Phoenix-Mesa-Scottsdale, AZ Metro Area<br />pop09E: 4151634","pop_growth: -0.1003330091<br />loghome_value: 11.17325<br />Metro Area: Pine Bluff, AR Metro Area<br />pop09E: 102091","pop_growth: -0.0086456434<br />loghome_value: 11.63691<br />Metro Area: Pittsburgh, PA Metro Area<br />pop09E: 2360259","pop_growth: -0.0220594896<br />loghome_value: 12.21948<br />Metro Area: Pittsfield, MA Metro Area<br />pop09E: 130168","pop_growth: -0.0352498067<br />loghome_value: 11.73607<br />Metro Area: Pocatello, ID Metro Area<br />pop09E: 88117","pop_growth: 0.1538071947<br />loghome_value: 11.44892<br />Metro Area: Ponce, PR Metro Area<br />pop09E: 263313","pop_growth: 0.0292899666<br />loghome_value: 12.37286<br />Metro Area: Portland-South Portland-Biddeford, ME Metro Area<br />pop09E: 514044","pop_growth: 0.1112145173<br />loghome_value: 12.53789<br />Metro Area: Portland-Vancouver-Beaverton, OR-WA Metro Area<br />pop09E: 2163436","pop_growth: 0.1597824930<br />loghome_value: 12.27186<br />Metro Area: Port St. Lucie, FL Metro Area<br />pop09E: 394775","pop_growth: 0.0704422382<br />loghome_value: 12.35751<br />Metro Area: Prescott, AZ Metro Area<br />pop09E: 209365","pop_growth: 0.0080327158<br />loghome_value: 12.59235<br />Metro Area: Providence-New Bedford-Fall River, RI-MA Metro Area<br />pop09E: 1602591","pop_growth: 0.1559417543<br />loghome_value: 12.32608<br />Metro Area: Provo-Orem, UT Metro Area<br />pop09E: 514553","pop_growth: 0.0682904781<br />loghome_value: 11.83573<br />Metro Area: Pueblo, CO Metro Area<br />pop09E: 153814","pop_growth: 0.1257582015<br />loghome_value: 12.17303<br />Metro Area: Punta Gorda, FL Metro Area<br />pop09E: 156043","pop_growth: -0.0190047414<br />loghome_value: 12.05350<br />Metro Area: Racine, WI Metro Area<br />pop09E: 199147","pop_growth: 0.2224314011<br />loghome_value: 12.15583<br />Metro Area: Raleigh-Cary, NC Metro Area<br />pop09E: 1042848","pop_growth: 0.1827084415<br />loghome_value: 11.86499<br />Metro Area: Rapid City, SD Metro Area<br />pop09E: 121029","pop_growth: 0.0370496949<br />loghome_value: 12.00579<br />Metro Area: Reading, PA Metro Area<br />pop09E: 401488","pop_growth: -0.0016849298<br />loghome_value: 12.50544<br />Metro Area: Redding, CA Metro Area<br />pop09E: 179387","pop_growth: 0.1059090979<br />loghome_value: 12.67106<br />Metro Area: Reno-Sparks, NV Metro Area<br />pop09E: 408760","pop_growth: 0.0578608542<br />loghome_value: 12.28118<br />Metro Area: Richmond, VA Metro Area<br />pop09E: 1209484","pop_growth: 0.1162113905<br />loghome_value: 12.75852<br />Metro Area: Riverside-San Bernardino-Ontario, CA Metro Area<br />pop09E: 4022939","pop_growth: 0.0546671276<br />loghome_value: 11.95697<br />Metro Area: Roanoke, VA Metro Area<br />pop09E: 296624","pop_growth: 0.1773854870<br />loghome_value: 12.03765<br />Metro Area: Rochester, MN Metro Area<br />pop09E: 180920","pop_growth: 0.0395184869<br />loghome_value: 11.70849<br />Metro Area: Rochester, NY Metro Area<br />pop09E: 1033026","pop_growth: -0.0244872937<br />loghome_value: 11.77759<br />Metro Area: Rockford, IL Metro Area<br />pop09E: 348203","pop_growth: 0.0132203405<br />loghome_value: 11.50691<br />Metro Area: Rocky Mount, NC Metro Area<br />pop09E: 145400","pop_growth: 0.0165053757<br />loghome_value: 11.68688<br />Metro Area: Rome, GA Metro Area<br />pop09E: 95239","pop_growth: 0.0985886535<br />loghome_value: 12.84318<br />Metro Area: Sacramento--Arden-Arcade--Roseville, CA Metro Area<br />pop09E: 2076579","pop_growth: -0.0507500351<br />loghome_value: 11.60368<br />Metro Area: Saginaw-Saginaw Township North, MI Metro Area<br />pop09E: 202814","pop_growth: 0.0574163637<br />loghome_value: 12.05989<br />Metro Area: St. Cloud, MN Metro Area<br />pop09E: 185628","pop_growth: 0.2090073465<br />loghome_value: 12.39172<br />Metro Area: St. George, UT Metro Area<br />pop09E: 130258","pop_growth: 0.0119420748<br />loghome_value: 11.57308<br />Metro Area: St. Joseph, MO-KS Metro Area<br />pop09E: 125274","pop_growth: 0.0006328745<br />loghome_value: 11.95247<br />Metro Area: St. Louis, MO-IL Metro Area<br />pop09E: 2803776","pop_growth: 0.0814092140<br />loghome_value: 12.21156<br />Metro Area: Salem, OR Metro Area<br />pop09E: 384379","pop_growth: 0.0675327596<br />loghome_value: 13.31925<br />Metro Area: Salinas, CA Metro Area<br />pop09E: 404922","pop_growth: 1.2118051480<br />loghome_value: 12.11286<br />Metro Area: Salisbury, MD Metro Area<br />pop09E: 118770","pop_growth: 0.0840185940<br />loghome_value: 12.33094<br />Metro Area: Salt Lake City, UT Metro Area<br />pop09E: 1090416","pop_growth: 0.0939404149<br />loghome_value: 11.32780<br />Metro Area: San Angelo, TX Metro Area<br />pop09E: 108321","pop_growth: 0.2033896498<br />loghome_value: 11.65269<br />Metro Area: San Antonio, TX Metro Area<br />pop09E: 1979686","pop_growth: 0.1003292746<br />loghome_value: 13.15464<br />Metro Area: San Diego-Carlsbad-San Marcos, CA Metro Area<br />pop09E: 2987543","pop_growth: -0.0296869758<br />loghome_value: 11.82992<br />Metro Area: Sandusky, OH Metro Area<br />pop09E: 77400","pop_growth: 0.1023608812<br />loghome_value: 13.40739<br />Metro Area: San Francisco-Oakland-Fremont, CA Metro Area<br />pop09E: 4218534","pop_growth: -0.1353514754<br />loghome_value: 11.38850<br />Metro Area: San Germ?n-Cabo Rojo, PR Metro Area<br />pop09E: 145966","pop_growth: 0.1049817720<br />loghome_value: 13.45955<br />Metro Area: San Jose-Sunnyvale-Santa Clara, CA Metro Area<br />pop09E: 1784130","pop_growth: -0.1931957138<br />loghome_value: 11.69441<br />Metro Area: San Juan-Caguas-Guaynabo, PR Metro Area<br />pop09E: 2598979","pop_growth: 0.0710595325<br />loghome_value: 13.18871<br />Metro Area: San Luis Obispo-Paso Robles, CA Metro Area<br />pop09E: 262149","pop_growth: 0.0852327335<br />loghome_value: 13.42291<br />Metro Area: Santa Cruz-Watsonville, CA Metro Area<br />pop09E: 251398","pop_growth: 0.0370470999<br />loghome_value: 12.56967<br />Metro Area: Santa Fe, NM Metro Area<br />pop09E: 143501","pop_growth: 0.0768843660<br />loghome_value: 13.24370<br />Metro Area: Santa Rosa-Petaluma, CA Metro Area<br />pop09E: 464218","pop_growth: 0.1497624392<br />loghome_value: 12.01793<br />Metro Area: Savannah, GA Metro Area<br />pop09E: 328544","pop_growth: 0.0145142791<br />loghome_value: 11.67164<br />Metro Area: Scranton--Wilkes-Barre, PA Metro Area<br />pop09E: 548901","pop_growth: 0.1415630672<br />loghome_value: 12.76940<br />Metro Area: Seattle-Tacoma-Bellevue, WA Metro Area<br />pop09E: 3306836","pop_growth: 0.1358047926<br />loghome_value: 12.21454<br />Metro Area: Sebastian-Vero Beach, FL Metro Area<br />pop09E: 131811","pop_growth: 0.0094450985<br />loghome_value: 11.90497<br />Metro Area: Sheboygan, WI Metro Area<br />pop09E: 114122","pop_growth: 0.0864486570<br />loghome_value: 11.46479<br />Metro Area: Sherman-Denison, TX Metro Area<br />pop09E: 117913","pop_growth: 0.1302626138<br />loghome_value: 11.60094<br />Metro Area: Shreveport-Bossier City, LA Metro Area<br />pop09E: 387436","pop_growth: 0.1705401780<br />loghome_value: 11.44465<br />Metro Area: Sioux City, IA-NE-SD Metro Area<br />pop09E: 142230","pop_growth: 0.1163395005<br />loghome_value: 11.84510<br />Metro Area: Sioux Falls, SD Metro Area<br />pop09E: 227384","pop_growth: 0.0119734861<br />loghome_value: 11.65962<br />Metro Area: South Bend-Mishawaka, IN-MI Metro Area<br />pop09E: 316883","pop_growth: 0.1762347163<br />loghome_value: 11.62268<br />Metro Area: Spartanburg, SC Metro Area<br />pop09E: 276544","pop_growth: 0.1993859483<br />loghome_value: 12.09514<br />Metro Area: Spokane, WA Metro Area<br />pop09E: 454927","pop_growth: 0.0168968602<br />loghome_value: 11.64308<br />Metro Area: Springfield, IL Metro Area<br />pop09E: 206509","pop_growth: -0.0979814873<br />loghome_value: 12.26858<br />Metro Area: Springfield, MA Metro Area<br />pop09E: 695157","pop_growth: 0.0940806436<br />loghome_value: 11.73126<br />Metro Area: Springfield, MO Metro Area<br />pop09E: 417635","pop_growth: -0.0378904395<br />loghome_value: 11.61096<br />Metro Area: Springfield, OH Metro Area<br />pop09E: 140419","pop_growth: 0.1122160942<br />loghome_value: 12.02695<br />Metro Area: State College, PA Metro Area<br />pop09E: 144306","pop_growth: 0.0968230443<br />loghome_value: 12.77987<br />Metro Area: Stockton, CA Metro Area<br />pop09E: 664641","pop_growth: 0.0241597857<br />loghome_value: 11.44892<br />Metro Area: Sumter, SC Metro Area<br />pop09E: 104441","pop_growth: 0.0144663282<br />loghome_value: 11.61458<br />Metro Area: Syracuse, NY Metro Area<br />pop09E: 645302","pop_growth: 0.0770530209<br />loghome_value: 12.05117<br />Metro Area: Tallahassee, FL Metro Area<br />pop09E: 351913","pop_growth: 0.1144415643<br />loghome_value: 12.13135<br />Metro Area: Tampa-St. Petersburg-Clearwater, FL Metro Area<br />pop09E: 2702390","pop_growth: 0.0034113065<br />loghome_value: 11.34569<br />Metro Area: Terre Haute, IN Metro Area<br />pop09E: 169733","pop_growth: 0.1069807198<br />loghome_value: 11.33380<br />Metro Area: Texarkana, TX-Texarkana, AR Metro Area<br />pop09E: 134812","pop_growth: -0.1079546472<br />loghome_value: 11.76679<br />Metro Area: Toledo, OH Metro Area<br />pop09E: 673545","pop_growth: 0.0194759208<br />loghome_value: 11.62178<br />Metro Area: Topeka, KS Metro Area<br />pop09E: 228761","pop_growth: 0.0136076580<br />loghome_value: 12.64980<br />Metro Area: Trenton-Ewing, NJ Metro Area<br />pop09E: 363778","pop_growth: 0.0293652486<br />loghome_value: 12.19045<br />Metro Area: Tucson, AZ Metro Area<br />pop09E: 990213","pop_growth: 0.0849387978<br />loghome_value: 11.66736<br />Metro Area: Tulsa, OK Metro Area<br />pop09E: 905004","pop_growth: 0.1592506975<br />loghome_value: 11.79660<br />Metro Area: Tuscaloosa, AL Metro Area<br />pop09E: 205860","pop_growth: 0.1297654110<br />loghome_value: 11.63956<br />Metro Area: Tyler, TX Metro Area<br />pop09E: 197631","pop_growth: -0.0006169526<br />loghome_value: 11.45530<br />Metro Area: Utica-Rome, NY Metro Area<br />pop09E: 293468","pop_growth: 0.0993803204<br />loghome_value: 11.65356<br />Metro Area: Valdosta, GA Metro Area<br />pop09E: 130888","pop_growth: 0.0759402411<br />loghome_value: 12.97317<br />Metro Area: Vallejo-Fairfield, CA Metro Area<br />pop09E: 406461","pop_growth: -0.1324806000<br />loghome_value: 11.40645<br />Metro Area: Victoria, TX Metro Area<br />pop09E: 113596","pop_growth: -0.0120908862<br />loghome_value: 12.03410<br />Metro Area: Vineland-Millville-Bridgeton, NJ Metro Area<br />pop09E: 155266","pop_growth: 0.0308945247<br />loghome_value: 12.36137<br />Metro Area: Virginia Beach-Norfolk-Newport News, VA-NC Metro Area<br />pop09E: 1669614","pop_growth: 0.1008591567<br />loghome_value: 12.28995<br />Metro Area: Visalia-Porterville, CA Metro Area<br />pop09E: 416299","pop_growth: 0.1515104874<br />loghome_value: 11.48453<br />Metro Area: Waco, TX Metro Area<br />pop09E: 228369","pop_growth: 0.3722139630<br />loghome_value: 11.76291<br />Metro Area: Warner Robins, GA Metro Area<br />pop09E: 130910","pop_growth: 0.1407790873<br />loghome_value: 12.95536<br />Metro Area: Washington-Arlington-Alexandria, DC-VA-MD-WV Metro Area<br />pop09E: 5332297","pop_growth: 0.0425790369<br />loghome_value: 11.66135<br />Metro Area: Waterloo-Cedar Falls, IA Metro Area<br />pop09E: 163040","pop_growth: 0.0412105079<br />loghome_value: 11.81894<br />Metro Area: Wausau, WI Metro Area<br />pop09E: 129803","pop_growth: -0.0284180435<br />loghome_value: 11.33857<br />Metro Area: Weirton-Steubenville, WV-OH Metro Area<br />pop09E: 122778","pop_growth: 0.0921877119<br />loghome_value: 12.25677<br />Metro Area: Wenatchee-East Wenatchee, WA Metro Area<br />pop09E: 106813","pop_growth: -0.0227170674<br />loghome_value: 11.32900<br />Metro Area: Wheeling, WV-OH Metro Area<br />pop09E: 145942","pop_growth: 0.0760148081<br />loghome_value: 11.62178<br />Metro Area: Wichita, KS Metro Area<br />pop09E: 596643","pop_growth: 0.0166416748<br />loghome_value: 11.34569<br />Metro Area: Wichita Falls, TX Metro Area<br />pop09E: 148502","pop_growth: -0.0188360995<br />loghome_value: 11.64483<br />Metro Area: Williamsport, PA Metro Area<br />pop09E: 117043","pop_growth: -0.1754779757<br />loghome_value: 12.18229<br />Metro Area: Wilmington, NC Metro Area<br />pop09E: 337583","pop_growth: 0.1232701655<br />loghome_value: 12.34844<br />Metro Area: Winchester, VA-WV Metro Area<br />pop09E: 120497","pop_growth: 0.3409858969<br />loghome_value: 11.85154<br />Metro Area: Winston-Salem, NC Metro Area<br />pop09E: 470584","pop_growth: 0.1653667317<br />loghome_value: 12.56024<br />Metro Area: Worcester, MA Metro Area<br />pop09E: 795726","pop_growth: 0.0681008599<br />loghome_value: 11.87200<br />Metro Area: Yakima, WA Metro Area<br />pop09E: 232911","pop_growth: 0.0566424001<br />loghome_value: 12.02155<br />Metro Area: York-Hanover, PA Metro Area<br />pop09E: 419563","pop_growth: -0.0466169217<br />loghome_value: 11.49984<br />Metro Area: Youngstown-Warren-Boardman, OH-PA Metro Area<br />pop09E: 571519","pop_growth: 0.0584427043<br />loghome_value: 12.49050<br />Metro Area: Yuba City, CA Metro Area<br />pop09E: 161637","pop_growth: 0.0950585623<br />loghome_value: 11.79283<br />Metro Area: Yuma, AZ Metro Area<br />pop09E: 188983"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,139,1)","opacity":1,"size":[5.18190814145035,6.08702112822991,7.27441515030626,5.21267082878734,7.66432818260763,7.61282726459212,5.13244095584968,7.54286784569076,4.9368225897542,5.65936004247658,4.52719812800004,6.19163031350852,6.12604047345889,4.82492412712963,5.53514541152602,6.34560888227165,5.35421019734669,13.6875753227381,5.79620969941765,4.97454062265021,6.77366212689375,9.16964272193753,7.48669916293911,10.8164024703855,5.1083459338082,5.55986258916317,7.44986286995478,5.02274327770779,4.77679729830291,6.24794539137431,5.39393782115392,5.13220297020234,5.12023570282393,5.67799078904586,8.25350972247821,4.72934255720425,5.16945603472153,5.33451382522527,6.93318939192032,12.9685557477082,5.91261847062498,4.8558606959515,5.64401470994749,7.76225173101028,6.27150146112363,4.71242350670699,8.28850603081229,5.08148060486288,5.47112172743932,6.36493108225078,6.91285067011581,4.62392967249207,3.77952755905512,4.33945456417543,5.70951083389727,5.55971897965645,5.94894498824089,7.08293193012161,9.25999659366364,5.39176032883917,6.7293018421787,4.55348381907671,17.12647953574,5.53462216046566,10.0640959765397,5.74585755477568,4.80618773969544,10.0050951991981,4.99646266866501,5.4569901517771,7.01491639620875,5.19925498886532,7.32450758611397,5.88363852993365,4.38595696502683,9.4590058317758,6.38090144610056,4.47913607877539,4.69542970508963,14.5179085857318,4.99151946578608,4.4766819942923,4.76106354641249,6.2426690107468,7.63299520948049,5.11396349865935,4.78619100056315,6.66350301220177,10.5153390794541,6.82041849844651,12.9050802678307,5.04236100728024,5.12836842925488,4.61416199334761,5.81784709102354,6.61414284679847,5.169592279512,5.18813324943188,4.81329261199824,5.42280098813487,4.56885676062179,7.35258449817468,5.84127437827491,6.11701217915014,6.14125684794765,4.66691706017393,5.39287585377502,4.90770472954931,6.14900622795601,6.48460536002242,4.94763775286909,6.45315653035133,5.42897231858833,5.06925562874272,4.69313169086261,5.87433849658326,5.88106282011599,6.36731059950593,7.75727247781584,4.73184156376691,5.72812858469002,5.30217140040015,4.95504767888209,4.82782764775588,4.67141930811195,5.03036689907836,7.46742588557207,4.48994796584543,5.65614359191547,5.93484463270793,7.26157346546428,5.26851654530033,7.03842598007438,4.52040433598851,5.63864906327215,5.7463053513251,5.09542087541321,6.7757644600213,4.86565171526008,8.40896336233972,5.03161534398542,6.18107084640021,4.3490289527081,4.66094274732909,5.44158238956094,14.0223985714915,5.86500153112554,6.29024753611475,4.87931430038519,9.35344966314657,5.09733358521753,4.70596599204751,5.19876135391434,6.78679570159179,4.82023071035558,8.62433389789135,5.22231783195872,5.18000952096403,5.08628640288772,5.39689708208653,5.08474931196728,4.85501580889639,5.25649336289451,6.03161833495151,4.80918088414011,9.86974066962403,5.60298003758195,6.21582424526341,5.94605358927225,5.32577528800259,7.22092080055141,4.69730937048116,4.97679676283847,5.73119244375912,5.39228883156973,5.39453597026592,6.89156676832125,6.678138992976,6.53173098018108,5.60402351008666,5.42261658505909,9.56304825573927,4.83174054086278,4.82364619667669,4.95224921112021,4.07554450328233,4.7671321153219,6.53297272500024,4.74953507180953,5.89247194627884,7.18112135594566,4.90053938211816,5.45209458602638,4.69869084304825,8.50719808152348,5.79283092615546,5.66263134069297,5.59754015935821,5.08166241496532,6.85541031850523,6.34417673999671,4.87860806660869,4.60882408413452,4.93524238462073,4.80896934775881,7.28111445285192,5.4238666630516,8.60974532841251,5.66125305604678,13.9197466843705,4.79862460901611,4.93929908650237,9.09342202292519,11.4996740775588,4.7562571627085,6.35432843580271,6.69847493832724,5.2710835066777,5.13932442147224,6.1948118900269,4.86990655494621,5.00346102070008,4.85336813073006,4.84802886169405,5.28006484210961,5.6930191382618,4.98639911119766,5.98954152594556,9.04749386537843,7.64323576768571,8.3406527379388,22.6771653543307,5.18877171782137,5.77813146671959,6.01391917977037,4.66994235727079,4.96114572012861,6.7361826328575,8.41761748919107,5.64616172277937,7.60919188698079,9.88497098564932,5.1971925897594,4.8185369839088,7.5156026048841,6.78646192070755,5.21091886369694,5.19576918732432,6.51572735479611,6.22528149952325,14.309871266623,12.5873087251247,4.72125291352506,10.3864925199803,4.97056420602284,4.56832874905594,5.76448740209738,6.72713745915661,10.0981156964896,6.31521094682602,5.48785992103533,9.19277842363982,6.72877213262907,5.1456811954761,5.16104430331524,5.43025200128829,8.10421060510194,4.89554462860488,6.34015656372944,5.31271923289771,6.36690806580261,8.45484921699061,12.4478483765026,5.9174958971044,5.32215798509842,8.08265137947378,6.13488542156861,5.08606175247273,4.64963307422854,9.96658339869201,5.45115453751355,5.35079094848599,4.97127950999856,4.93099871484535,10.9941863770863,6.27608739367929,6.35282387337141,4.87621037727369,8.20713698840709,4.78193977750734,9.81647234201556,11.2314721069072,4.42702195344016,12.6589396961113,5.09015736757523,9.50152605505352,10.7201947076429,5.75892690489753,5.70681050466295,5.07222565816735,6.56247570001706,6.05448006866725,6.83706337659435,11.6267080617103,4.98355554659624,4.83531611503409,4.86878572648905,6.28765522950404,5.06288183729245,5.58497567851988,6.00541460509558,5.8266313633618,6.53068142380021,5.47195557509033,7.26066507561187,6.39918640230085,5.04944941592166,5.0781088807163,7.17664501742257,4.74459278749258,7.1223056611552,6.14975340579374,10.8598704793035,5.25188942163862,5.00692980418166,7.20137366834318,5.59218321027158,6.19668905379043,7.98738721645599,7.79106050780414,5.46832057205231,5.42153279876164,5.90347208542939,4.97627466670956,6.35848073268298,4.83058802244681,5.15570839912626,9.30877390234087,6.39435285232961,5.59013431423763,4.97644872405674,13.7763460925284,5.20819741504662,4.96765883626858,4.91028687284319,4.76759222423457,5.08998396179152,6.98150543126077,5.10835305966118,4.86119632218613,6.0917968595328,4.89102164109887,6.58405239099188,7.52424277815928,5.61373396099641,6.40614608474987,6.90632536135512,5.19886810034285,5.37088093284661],"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,139,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"x":[-0.567747199240083,-0.552388480648808,-0.537029762057533,-0.521671043466258,-0.506312324874984,-0.490953606283709,-0.475594887692434,-0.460236169101159,-0.444877450509885,-0.42951873191861,-0.414160013327335,-0.39880129473606,-0.383442576144786,-0.368083857553511,-0.352725138962236,-0.337366420370961,-0.322007701779687,-0.306648983188412,-0.291290264597137,-0.275931546005863,-0.260572827414588,-0.245214108823313,-0.229855390232038,-0.214496671640764,-0.199137953049489,-0.183779234458214,-0.168420515866939,-0.153061797275665,-0.13770307868439,-0.122344360093115,-0.10698564150184,-0.0916269229105657,-0.0762682043192909,-0.0609094857280162,-0.0455507671367414,-0.0301920485454668,-0.014833329954192,0.000525388637082735,0.0158841072283575,0.0312428258196322,0.046601544410907,0.0619602630021817,0.0773189815934564,0.0926777001847312,0.108036418776006,0.123395137367281,0.138753855958555,0.15411257454983,0.169471293141105,0.18483001173238,0.200188730323654,0.215547448914929,0.230906167506204,0.246264886097479,0.261623604688753,0.276982323280028,0.292341041871303,0.307699760462578,0.323058479053852,0.338417197645127,0.353775916236402,0.369134634827676,0.384493353418951,0.399852072010226,0.415210790601501,0.430569509192775,0.44592822778405,0.461286946375325,0.4766456649666,0.492004383557874,0.507363102149149,0.522721820740424,0.538080539331699,0.553439257922973,0.568797976514248,0.584156695105523,0.599515413696798,0.614874132288072,0.630232850879347,0.645591569470622],"y":[11.5482086204018,11.5579952758773,11.5677819313529,11.5775685868284,11.587355242304,11.5971418977795,11.6069285532551,11.6167152087307,11.6265018642062,11.6362885196818,11.6460751751573,11.6558618306329,11.6656484861084,11.675435141584,11.6852217970596,11.6950084525351,11.7047951080107,11.7145817634862,11.7243684189618,11.7341550744373,11.7439417299129,11.7537283853885,11.763515040864,11.7733016963396,11.7830883518151,11.7928750072907,11.8026616627662,11.8124483182418,11.8222349737174,11.8320216291929,11.8418082846685,11.851594940144,11.8613815956196,11.8711682510951,11.8809549065707,11.8907415620462,11.9005282175218,11.9103148729974,11.9201015284729,11.9298881839485,11.939674839424,11.9494614948996,11.9592481503751,11.9690348058507,11.9788214613263,11.9886081168018,11.9983947722774,12.0081814277529,12.0179680832285,12.027754738704,12.0375413941796,12.0473280496552,12.0571147051307,12.0669013606063,12.0766880160818,12.0864746715574,12.0962613270329,12.1060479825085,12.115834637984,12.1256212934596,12.1354079489352,12.1451946044107,12.1549812598863,12.1647679153618,12.1745545708374,12.1843412263129,12.1941278817885,12.2039145372641,12.2137011927396,12.2234878482152,12.2332745036907,12.2430611591663,12.2528478146418,12.2626344701174,12.272421125593,12.2822077810685,12.2919944365441,12.3017810920196,12.3115677474952,12.3213544029707],"text":["pop_growth: -0.5677471992<br />loghome_value: 11.54821<br />pop09E: 1","pop_growth: -0.5523884806<br />loghome_value: 11.55800<br />pop09E: 1","pop_growth: -0.5370297621<br />loghome_value: 11.56778<br />pop09E: 1","pop_growth: -0.5216710435<br />loghome_value: 11.57757<br />pop09E: 1","pop_growth: -0.5063123249<br />loghome_value: 11.58736<br />pop09E: 1","pop_growth: -0.4909536063<br />loghome_value: 11.59714<br />pop09E: 1","pop_growth: -0.4755948877<br />loghome_value: 11.60693<br />pop09E: 1","pop_growth: -0.4602361691<br />loghome_value: 11.61672<br />pop09E: 1","pop_growth: -0.4448774505<br />loghome_value: 11.62650<br />pop09E: 1","pop_growth: -0.4295187319<br />loghome_value: 11.63629<br />pop09E: 1","pop_growth: -0.4141600133<br />loghome_value: 11.64608<br />pop09E: 1","pop_growth: -0.3988012947<br />loghome_value: 11.65586<br />pop09E: 1","pop_growth: -0.3834425761<br />loghome_value: 11.66565<br />pop09E: 1","pop_growth: -0.3680838576<br />loghome_value: 11.67544<br />pop09E: 1","pop_growth: -0.3527251390<br />loghome_value: 11.68522<br />pop09E: 1","pop_growth: -0.3373664204<br />loghome_value: 11.69501<br />pop09E: 1","pop_growth: -0.3220077018<br />loghome_value: 11.70480<br />pop09E: 1","pop_growth: -0.3066489832<br />loghome_value: 11.71458<br />pop09E: 1","pop_growth: -0.2912902646<br />loghome_value: 11.72437<br />pop09E: 1","pop_growth: -0.2759315460<br />loghome_value: 11.73416<br />pop09E: 1","pop_growth: -0.2605728274<br />loghome_value: 11.74394<br />pop09E: 1","pop_growth: -0.2452141088<br />loghome_value: 11.75373<br />pop09E: 1","pop_growth: -0.2298553902<br />loghome_value: 11.76352<br />pop09E: 1","pop_growth: -0.2144966716<br />loghome_value: 11.77330<br />pop09E: 1","pop_growth: -0.1991379530<br />loghome_value: 11.78309<br />pop09E: 1","pop_growth: -0.1837792345<br />loghome_value: 11.79288<br />pop09E: 1","pop_growth: -0.1684205159<br />loghome_value: 11.80266<br />pop09E: 1","pop_growth: -0.1530617973<br />loghome_value: 11.81245<br />pop09E: 1","pop_growth: -0.1377030787<br />loghome_value: 11.82223<br />pop09E: 1","pop_growth: -0.1223443601<br />loghome_value: 11.83202<br />pop09E: 1","pop_growth: -0.1069856415<br />loghome_value: 11.84181<br />pop09E: 1","pop_growth: -0.0916269229<br />loghome_value: 11.85159<br />pop09E: 1","pop_growth: -0.0762682043<br />loghome_value: 11.86138<br />pop09E: 1","pop_growth: -0.0609094857<br />loghome_value: 11.87117<br />pop09E: 1","pop_growth: -0.0455507671<br />loghome_value: 11.88095<br />pop09E: 1","pop_growth: -0.0301920485<br />loghome_value: 11.89074<br />pop09E: 1","pop_growth: -0.0148333300<br />loghome_value: 11.90053<br />pop09E: 1","pop_growth: 0.0005253886<br />loghome_value: 11.91031<br />pop09E: 1","pop_growth: 0.0158841072<br />loghome_value: 11.92010<br />pop09E: 1","pop_growth: 0.0312428258<br />loghome_value: 11.92989<br />pop09E: 1","pop_growth: 0.0466015444<br />loghome_value: 11.93967<br />pop09E: 1","pop_growth: 0.0619602630<br />loghome_value: 11.94946<br />pop09E: 1","pop_growth: 0.0773189816<br />loghome_value: 11.95925<br />pop09E: 1","pop_growth: 0.0926777002<br />loghome_value: 11.96903<br />pop09E: 1","pop_growth: 0.1080364188<br />loghome_value: 11.97882<br />pop09E: 1","pop_growth: 0.1233951374<br />loghome_value: 11.98861<br />pop09E: 1","pop_growth: 0.1387538560<br />loghome_value: 11.99839<br />pop09E: 1","pop_growth: 0.1541125745<br />loghome_value: 12.00818<br />pop09E: 1","pop_growth: 0.1694712931<br />loghome_value: 12.01797<br />pop09E: 1","pop_growth: 0.1848300117<br />loghome_value: 12.02775<br />pop09E: 1","pop_growth: 0.2001887303<br />loghome_value: 12.03754<br />pop09E: 1","pop_growth: 0.2155474489<br />loghome_value: 12.04733<br />pop09E: 1","pop_growth: 0.2309061675<br />loghome_value: 12.05711<br />pop09E: 1","pop_growth: 0.2462648861<br />loghome_value: 12.06690<br />pop09E: 1","pop_growth: 0.2616236047<br />loghome_value: 12.07669<br />pop09E: 1","pop_growth: 0.2769823233<br />loghome_value: 12.08647<br />pop09E: 1","pop_growth: 0.2923410419<br />loghome_value: 12.09626<br />pop09E: 1","pop_growth: 0.3076997605<br />loghome_value: 12.10605<br />pop09E: 1","pop_growth: 0.3230584791<br />loghome_value: 12.11583<br />pop09E: 1","pop_growth: 0.3384171976<br />loghome_value: 12.12562<br />pop09E: 1","pop_growth: 0.3537759162<br />loghome_value: 12.13541<br />pop09E: 1","pop_growth: 0.3691346348<br />loghome_value: 12.14519<br />pop09E: 1","pop_growth: 0.3844933534<br />loghome_value: 12.15498<br />pop09E: 1","pop_growth: 0.3998520720<br />loghome_value: 12.16477<br />pop09E: 1","pop_growth: 0.4152107906<br />loghome_value: 12.17455<br />pop09E: 1","pop_growth: 0.4305695092<br />loghome_value: 12.18434<br />pop09E: 1","pop_growth: 0.4459282278<br />loghome_value: 12.19413<br />pop09E: 1","pop_growth: 0.4612869464<br />loghome_value: 12.20391<br />pop09E: 1","pop_growth: 0.4766456650<br />loghome_value: 12.21370<br />pop09E: 1","pop_growth: 0.4920043836<br />loghome_value: 12.22349<br />pop09E: 1","pop_growth: 0.5073631021<br />loghome_value: 12.23327<br />pop09E: 1","pop_growth: 0.5227218207<br />loghome_value: 12.24306<br />pop09E: 1","pop_growth: 0.5380805393<br />loghome_value: 12.25285<br />pop09E: 1","pop_growth: 0.5534392579<br />loghome_value: 12.26263<br />pop09E: 1","pop_growth: 0.5687979765<br />loghome_value: 12.27242<br />pop09E: 1","pop_growth: 0.5841566951<br />loghome_value: 12.28221<br />pop09E: 1","pop_growth: 0.5995154137<br />loghome_value: 12.29199<br />pop09E: 1","pop_growth: 0.6148741323<br />loghome_value: 12.30178<br />pop09E: 1","pop_growth: 0.6302328509<br />loghome_value: 12.31157<br />pop09E: 1","pop_growth: 0.6455915695<br />loghome_value: 12.32135<br />pop09E: 1"],"type":"scatter","mode":"lines","name":"fitted values","line":{"width":3.77952755905512,"color":"rgba(255,140,0,1)","dash":"solid"},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":31.9402241594022,"r":13.2835201328352,"b":36.5296803652968,"l":49.813200498132},"plot_bgcolor":"rgba(255,255,255,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.6,1],"tickmode":"array","ticktext":["-0.5","-0.3","-0.1","0.0","0.1","0.3","0.5"],"tickvals":[-0.5,-0.3,-0.1,0,0.1,0.3,0.5],"categoryorder":"array","categoryarray":["-0.5","-0.3","-0.1","0.0","0.1","0.3","0.5"],"nticks":null,"ticks":"outside","tickcolor":"rgba(0,0,0,1)","ticklen":-11.2909921129099,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":true,"linecolor":"rgba(0,0,0,1)","linewidth":0.531340805313408,"showgrid":false,"gridcolor":null,"gridwidth":0,"zeroline":false,"anchor":"y","title":{"text":"<b> Population Growth 2009-2018 <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[11.0060060496074,13.5763850540521],"tickmode":"array","ticktext":["11.5","12.0","12.5","13.0","13.5"],"tickvals":[11.5,12,12.5,13,13.5],"categoryorder":"array","categoryarray":["11.5","12.0","12.5","13.0","13.5"],"nticks":null,"ticks":"","tickcolor":null,"ticklen":-11.2909921129099,"tickwidth":0,"showticklabels":true,"tickfont":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(201,201,201,1)","gridwidth":1.16230801162308,"zeroline":false,"anchor":"x","title":{"text":"<b> Log Median Home Value 2009 <\/b>","font":{"color":"rgba(0,0,0,1)","family":"","size":15.9402241594022}},"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":18.2648401826484}},"hovermode":"closest","width":1100,"height":500,"barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"37182ea14fe9":{"x":{},"y":{},"label":{},"size":{},"type":"scatter"},"371845a26b92":{"x":{},"y":{},"label":{},"size":{}}},"cur_data":"37182ea14fe9","visdat":{"37182ea14fe9":["function (y) ","x"],"371845a26b92":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script>